교통 잡음으로부터 표면파 추출을 위한 지진파 간섭법의 비교
Copyright ⓒ The Geological Society of Korea 2024
초록
도로를 주행하는 차량으로 발생하는 교통 잡음을 활용하여 표면파 경험 그린함수를 추출하기 위해 네 가지 지진파 간섭법을 비교 분석하였다. 단순 및 초기백색화 상호상관, 역합성곱, 상호간섭 방법 모두 짧은 시간의 지진기록으로부터 표면파를 효과적으로 추출할 수 있음을 확인하였다. 초기백색화를 적용한 상호상관법과 상호간섭법은 단순 상호상관법보다 더 명확한 표면파 경험 그린함수를 제공하였다. 역합성곱 방법은 비물리적 혼선이 상대적으로 두드러졌다. 분산 분석 결과, 주파수 10 Hz 이상에서 수치모델의 전단파 속도 400 m/s와 700 m/s에 상응하는 표면파의 기본 모드와 고차 모드를 명확히 확인할 수 있었다. 야외 실험 결과, 200 - 300 m/s 범위의 일정한 위상 속도를 확인하였으며, 이는 실험 지역 지표층의 전단파 속도를 적절하게 반영한 것으로 보인다. 교통 잡음을 이용한 지진파 간섭법이 천부 지층 전단파 속도 구조를 파악하는 데 효과적임을 확인하였다.
Abstract
This study compares and analyzes four seismic interferometry methods to extract empirical Green’s functions of surface waves from traffic noise generated by vehicles traveling on roads. The cross-correlation, deconvolution, and cross-coherency methods were evaluated using synthetic seismic records and field data. All methods effectively extracted surface waves from short-duration seismic records. Pre-whitened cross-correlation and cross-coherency methods provided clearer empirical Green's functions than raw cross-correlation. The deconvolution method exhibited non-physical crosstalk relatively. Dispersion analysis confirmed the fundamental and higher modes of surface waves above 10 Hz, corresponding to shear wave velocities of 400 m/s and 700 m/s in the numerical model. Field experiments showed consistent phase velocities in the range of 200 - 300 m/s, reflecting the shear wave velocity of the surficial layers in the study area. The findings confirm that seismic interferometry using traffic noise is effective for determining the shear wave velocity structure of shallow subsurface layers.
Keywords:
traffic noise, seismic interferometry, surface waves, shear-wave velocity, shallow subsurface layers키워드:
교통 잡음, 지진파 간섭법, 표면파, 전단파 속도, 천부 지층1. 서 론
표면파는 진동 주기에 따라 서로 다른 파장을 가지며, 이로 인해 지구 표면을 따라 진행하면서 서로 다른 깊이 범위에서 진동한다. 이 특성으로 인해 표면파는 깊이에 따라 다른 속력으로 전파하며, 지표면 하부의 전단파 속도 구조에 민감하게 반응한다. 서로 다른 주기에서의 표면파 속도를 측정하는 분산 분석으로 지구 규모(Meier et al., 2007)와 지역 규모(Yao et al., 2006) 및 산업 규모(Park et al., 1999) 등과 같은 다양한 깊이 범위에서 지구 내부의 속도 구조를 규명할 수 있다. 표면파 기록은 보통 상대적으로 얕은 깊이에서 발생하는 자연지진이나 제어 지진원을 이용한 능동적인 탐사를 통하여 얻어진다. 한편, 지진기록의 배경 잡음으로부터 표면파를 추출하는 연구가 다양한 규모에서 각광을 받으면서, 이제 지진 기록의 대부분을 차지하는 배경 잡음이 표면파에 대한 중요한 정보원이 되었다(Shapiro and Campillo, 2004; Sabra et al., 2005; Shapiro et al., 2005; Kang and Shin, 2006).
천부 지층의 전단파 속도 분포는 지진동 증폭과 같은 부지 효과에 크게 영향을 미치기 때문에 지진재해도 평가에서 중요한 요소를 차지한다. 특히 상대적으로 좁은 영역을 갖는 도시 지역의 지진위험도는 그 밖의 지역에 비하여 매우 커서, 부지 효과에 따른 지진 소구역화가 도시 지역의 지진재해도 평가의 신뢰도와 밀접한 관련이 있다. 이와 같은 도시 지역 천부 지층의 전단파 속도 정보의 중요성에도 불구하고, 도시 지역은 많은 구조물의 분포와 인간 활동의 밀집으로 인하여 지질조사나 물리탐사 등을 통한 지표면 하부 지층에 대한 정보를 파악하기가 어려운 한계를 갖고 있다. 반면에 도시 지역의 풍부한 교통 잡음 신호는 긴 지속성을 가지며 도로 주변에서 쉽게 기록할 수 있다. 교통 잡음은 일반적으로 강한 고주파 표면파를 포함하기 때문에 천부 지층의 전단파 속도 분포를 파악하는데 효과적인 자료이다(Nakata et al., 2011; Behm et al., 2014; Cheng et al., 2019; Yan et al., 2021; Mi et al., 2022; Shao et al., 2022; Cao et al., 2023).
교통 잡음 신호를 처리하기 위하여 일반적으로 서로 다른 두 지점의 센서 기록에 대한 간섭 효과를 분석하기 때문에, 이를 지진파 간섭법(seismic interferometry)이라고 부른다. 두 지점 사이의 간섭을 계산하기 위하여, 보통 긴 길이의 연속적인 잡음 기록을 여러 개의 짧은 구간으로 분할한다. 일관된 간섭 효과는 신호가 되어 누적할 때 진폭이 배가되므로, 각 구간의 간섭 계산 결과를 더하여 신호대 잡음비를 향상시켜서 최종적으로 표면파의 존재를 추정할 수 있다. 이와 같은 방법은 매우 긴 교통 잡음 기록을 필요로 하기 때문에, 특히 도시 지역에서는 공간의 제약으로 인하여 효율이 낮아진다.
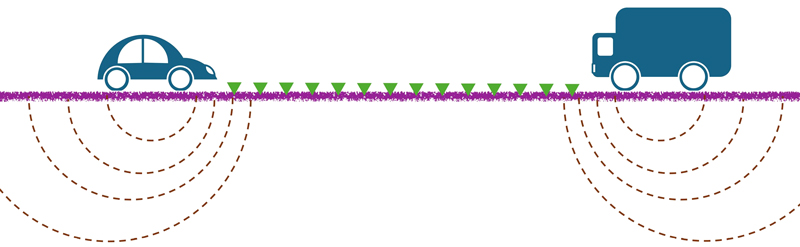
이 연구에서는 자동차가 이동하는 도로를 따라 배치된 선형 지진계 배열을 가정하고, 이를 통해 기록한 연속적인 교통 잡음 신호로부터 표면파를 추출하는 방법을 비교하고 분석한다(그림 1). 먼저, 연속적인 신호의 길이가 수초에서 수십 초에 이르는 매우 짧은 시간에 대하여 효과적으로 표면파를 추출할 수 있는 상호상관(cross-correlation), 역합성곱(deconvolution), 상호간섭(cross-coherency)의 세 가지 지진파 간섭법을 소개한다. 자동차의 이동으로 도로 표면을 따라 불규칙하게 발생하는 충격을 교통 잡음 신호원으로 가정하고, 이들 진원으로부터 전파하는 지진파의 수치모의를 수행한다. 그 결과로 얻은 합성 지진자료에 대하여 지진파 간섭법을 적용한다. 도시 지역의 복잡한 교통 잡음 환경을 가정하여, 잡음 수준의 복잡한 정도가 지진파 간섭법 적용 결과에 미치는 영향을 비교한다. 다음으로, 야외 실험을 통하여 얻은 교통 잡음 기록을 사용하여 이들 방법을 시험하고, 각각의 특징에 대하여 토의한다.
2. 방 법
지진학에 소개된 지진파 간섭법으로 가장 일반적인 방법은 두 지점에서 동시에 기록한 배경잡음을 상호상관(cross-correlation) 분석하여 이들 지점 사이의 레일리파(Rayleigh waves) 그린함수(Green’s function)를 추출하는 방법이다(Campillo and Paul, 2003). 가상의 지진원에 위치하는 센서 A에서의 기록 fA(t)를 센서 B에서의 기록 fB(t)와 상관시키면 두 지점 사이의 간섭기록 gBA(t)를 다음과 같이 얻을 수 있다:
| (1) |
이 식에서 ∗는 역방향 시계열과의 상관관계에 해당하는 합성곱(convolution)을 나타낸다. 시간 영역에서의 합성곱은 주파수 영역에서 곱하기와 같으므로, 식(1)을 주파수 영역에 대하여 나타내면 다음과 같다:
| (2) |
이 식에서 ω(=2πf)는 각주파수(angular frequency)이고, GBA, FB, FA는 각각 gBA, fB, fA의 푸리에(Fourier) 변환 결과이며, FA는 FA의 켤레복소수(complex conjugate)를 나타낸다. 이후 설명에서는 모두 주파수 영역에서의 연산을 가정하여 주파수에 대한 명시적인 언급 없이 함수를 표현한다.
지진 배경잡음에 대한 상호상관 분석의 배경에는 배경잡음의 근원에 대한 에너지와 그 분포의 균일성에 대한 가정을 전제로 한다(Lobkis and Weaver, 2001; Campillo and Paul, 2003; Snieder, 2004). 다양한 위치에서 크고 작은 잡음원이 존재하는 실제 조건에서 이 가정은 충족되기 어렵다. 따라서 실제 지진기록을 사용하는 대부분의 연구는 자료의 전처리 단계에서 인위적인 균일화를 시도한다(Sabra et al., 2005; Shapiro et al., 2005; Kang and Shin, 2006; Bensen et al., 2007). 이 연구에서는 다음과 같이 각 기록의 진폭스펙트럼으로 스펙트럼을 나누어서 서로 다른 주파수에서의 스펙트럼 파워를 균일하게 만드는 초기백색화(pre-whitening)를 실시하였다:
| (3) |
한편, 식(2)에서 지점 A에서의 가상 지진원에 대한 지점 B에서의 응답은 센서 A의 크기에 좌우되는 결과를 나타낸다. 따라서 센서 A에서의 단위 크기에 대한 센서 B의 비는 두 지점 사이의 상관 정도를 나타낸다. 두 센서 지점 사이의 단위 크기를 갖는 그린함수를 얻기 위하여 |FA|2=FAFA로 식(2)의 양변을 나누면 GBA를 다음과 같이 정규화할 수 있다.
| (4) |
식(4)의 정규화 그린함수 〈GAB〉는 결국 FA에 대한 FB의 역합성곱(deconvolution)을 나타낸다.
한편, 식(2)는 상호상관 스펙트럼을 나타내며, 그 결과는 배경잡음을 포함하는 대상 지진기록들의 평균 스펙트럼 밀도의 크기에 비례한다. 실제 상황에서 배경잡음은 모든 방향에 대하여 균일하지도 않고 완전한 백색 잡음도 아니기 때문에 일반적으로 정규화를 거친 결과를 사용한다(Prieto et al., 2009). 공간 자기상관(spatial autocorrelation; SPAC)으로 알려진 방법(Aki, 1957)에서 정규화는 다음과 같이 이루어진다(Prieto et al., 2009):
| (5) |
식(5)의 정규화는 상호상관을 수행하는 두 지점에 대한 각각의 크기에 대하여 이루어지기 때문에 상호간섭(cross-cherency)이라고 한다. 상호간섭에 대한 정규화는 상호상관이나 역합성곱에 앞서서 잡음의 주파수 의존성을 제거하기 위하여 수행되는 식(3)의 초기백색화의 결과와 동등하다. 여러 연구에서 경험 그린함수를 추출하기 위하여 사용되는 상호간섭을 이용하는 SPAC 방법과 시간 영역 상호상관 방법이 일관하는 결과를 보인다는 것은 잘 알려져 있다(Chávez-García and Luzón, 2005; Yokoi and Margaryan, 2008; Prieto et al., 2009).
식(3), (4), (5)에 대한 실제 계산에서는 분모가 0에 가까워질 때 발생할 수 있는 문제를 피하여야 한다. 이 연구에서는 각 식이 갖는 분모 값 최대치의 1만분의 1(= 0.0001)에 해당하는 값을 더하여 계산의 불안정성과 잡음의 증폭을 방지한다.
3. 실 험
도로에서 자동차 운행으로 지반을 통해 전파되는 잡음 신호로부터 표면파를 추출하기 위하여 제시한 세 가지 지진파 간섭법을 실험을 통하여 설명한다. 이 실험은 자동차 운행을 가정한 수치모의 합성 지진기록을 이용한 실험과 야외 관측을 통하여 획득한 지진기록을 이용한 실험의 두 가지 방식으로 진행한다. 수치모의 합성 지진기록은 가능한 잡음의 조건을 제어함으로써 각 방법의 특징을 비교할 수 있는 장점이 있다. 반면에 수치모의는 실제 상황을 단순화한 가정에 기반을 두고 있기 때문에, 수치 오류의 포함이나 수치모의에서 다룰 수 없는 여러 복잡한 외부 요인들의 결합 효과를 설명할 수 없는 한계가 있다. 이에 따라 실제 자동차 운행이 이루어지는 도로를 따라 선형적으로 배열한 센서로부터 획득한 지진기록을 이용하여 실험을 보완한다. 야외 관측 실험을 통하여 수치모의 합성 지진기록을 이용한 실험에서 파악한 각 지진파 간섭법의 특징이 어떻게 나타나는지 살펴본다.
3.1. 수치모의 합성 지진자료
일반 도로에서 자동차 운행을 가정한 지진 잡음 신호를 얻기 위하여, 지표층과 하부의 반무한 공간으로 이루어진 단순 수치 모델을 구성하였다(그림 2a). 수치 모델은 수평 150 m와 깊이 50 m의 2차원 수직 단면을 가정한 것이다. 지표층은 전체적으로 깊이가 10 m이며, 모델의 중앙부를 차지하는 수평거리 60 - 90 m 사이에서는 근소한 지중 변화를 표현하기 위하여 깊이가 15 m로 변하도록 하였다. 모델에서 설정한 압축파 속력(υP)과 전단파 속력(υS) 및 밀도(ρ)는 지표층에서 각각 1000 m/s, 400 m/s, 1300 kg/m3 이고, 그 하부는 각각 1300 m/s, 700 m/s, 2000 kg/m3 이다. 지층의 감쇄 특성은 고려하지 않았다. 도로를 가정하는 모델의 표면을 따라 수평거리 40 - 110 m 사이에 1 m 간격으로 71개의 관측점을 선형 배열하였다. 도로를 따라 수진점 배열과 나란한 자동차의 주행을 가정하기 위하여, 모델 수평거리 10 - 140 m 사이에 걸쳐 서로 다른 지연 시간에 따라 발진하는 임의 간격의 60개 점 진원을 선형 배열하였다. 이들 점 진원은 차량의 주행으로 불규칙한 임의의 지점에서 충격이 발생하여 지진에너지를 발생시키는 위치임을 가정한 것이다.
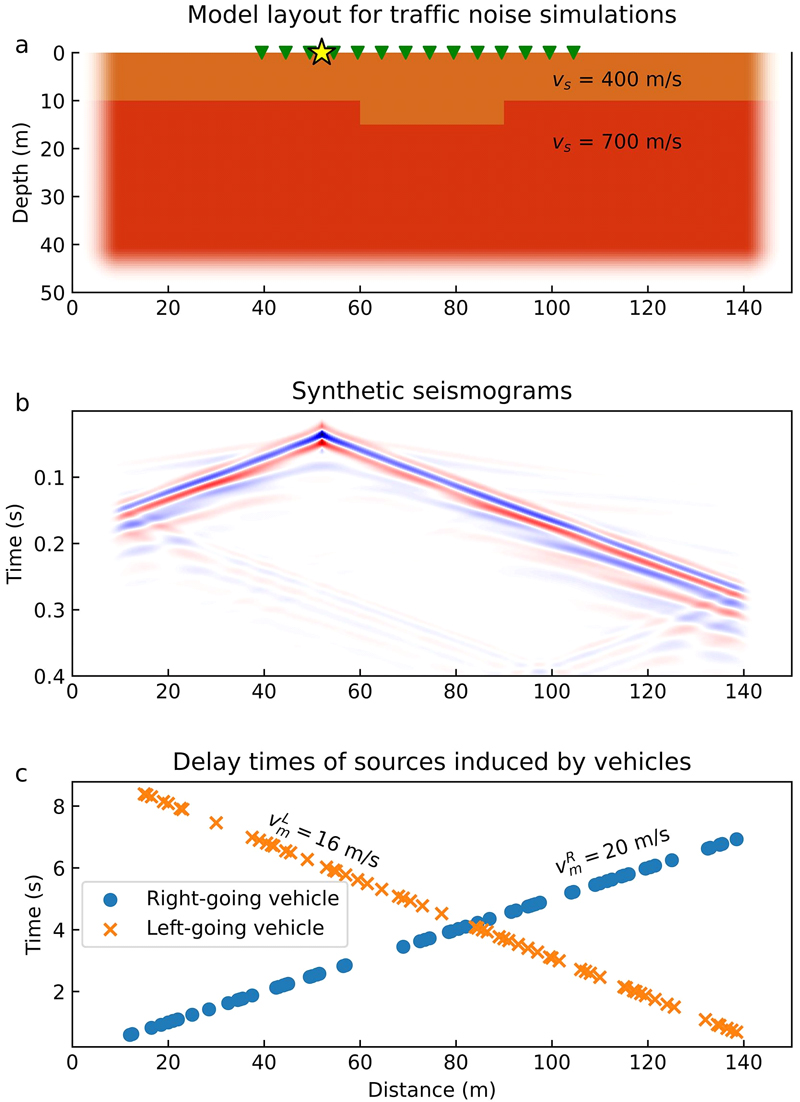
Traffic noise simulation model. (a) Geophone layout denoted with triangles and subsurface shear-wave velocity model, of which left, right, and bottom margins are graphically tapered to represent absorbing boundary conditions for numerical computations; (b) An example of synthetic seismograms in which the seismic energy generated at the source indicated by the star in the figure above is recorded using a geophone array; (c) Delay times of random seismic sources induced by vehicles moving with different speeds in opposite directions.
Kang and Baag (2004a, 2004b)이 사용한 상수 격자 및 시간 간격(constant grid and time step; CGTS) 유한차분법을 이용하여 지진파 전파 수치모의를 수행하였다. 유한차분 수치모의를 위하여 모델의 격자 간격을 0.5 m로 균일하게 설정하였다. 우세주파수가 30 Hz인 Ricker 파소를 진원시간함수로 사용하여, 0.0002초의 시간 간격으로 총 2초 길이의 지속시간을 갖는 합성 지진기록을 계산하였다. 수치모의에서 각 진원은 지면에 가해지는 수직적인 하중을 가정하여 해당 수치모의 격자의 수직응력(τzz)에만 진원시간함수를 적용하였다. 그림 2a에서 별 표시된 위치의 점 진원에 대하여 계산한 합성 지진기록을 그림 2b에 제시하였다. 그림 2b에서 가장 큰 진폭을 가지고 선형으로 분포하는 위상은 S파이며, 거리가 멀어질수록 뚜렷해지는 표면파의 발달을 확인할 수 있다. 합성 지진기록의 양 끝으로부터 반대 방향으로 선형성을 보이는 약한 위상은 모델의 경계에서 발생한 비물리적인 수치적인 반사파이다.
도로를 서로 반대 방향으로 진행하는 상황을 가정한다(그림 1). 속력 20 m/s (= 72 km/h)의 자동차가 수치 모델의 오른쪽 방향으로 진행하고, 속력 16 m/s (= 57.6 km/h)의 자동차가 왼쪽 방향으로 진행한다. 이와 같은 자동차의 주행에 따라 임의의 위치에서 발생한 지면의 충격을 점 진원으로 가정하였을 때, 각 진원 위치에서의 발진 시각은 자동차의 속력에 관계되는 지연 시간을 갖는다(그림 2c). 양 방향으로 진행하는 두 대의 자동차에 대하여, 임의 위치의 120개(60개 × 2대) 점 진원 각각에 대하여 지진파 전파 수치모의를 수행하였다. 수치모의 결과에 각 진원 위치의 해당 지연시간을 반영한 후, 각 관측점에서 합성 지진기록을 모두 더하였다(Cao et al., 2023). 그림 3은 71개 관측점에 대하여 합성한 속도 성분의 교통 잡음 지진 기록 단면을 나타낸다.
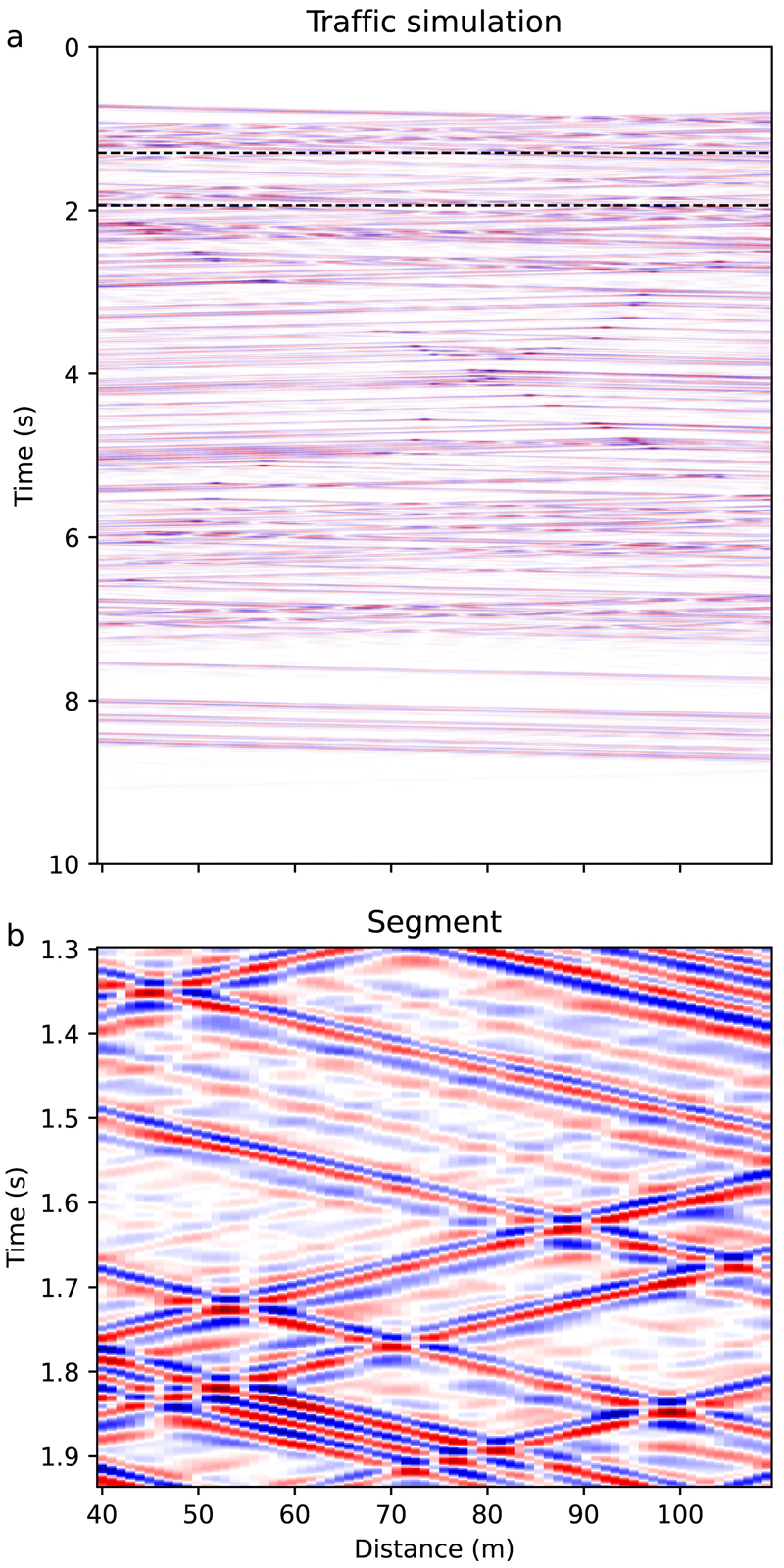
Seismic records from traffic simulation. Seismic sections over time and distance are the result of stacking seismic waveforms recorded by the geophone array for each source, reflecting its delay time shown in Fig. 2c. The interval between dashed lines in (a) indicates a segment selected to perform seismic interferometry, which is shown as an enlarged section in (b).
앞 절에서 소개한 세 가지의 지진파 간섭법을 자동차 이동 합성 지진 잡음 자료에 적용하여 각 방법의 특징을 분석하였다. 이 가운데 상호상관법은 초기백색화 적용 전후를 비교하기 위하여 각각 식(2)와 (3)을 분리하여 적용하였기 때문에, 실질적인 비교는 모두 네 가지 경우에 해당한다. 그림 2b에서 확인한 것처럼, 원거리 장에서 표면파의 발달이 충분한 기록을 분석할 수 있도록 그림 3a에서 1.296 - 1.938초 사이의 구간을 선택하였다(그림 3b). 이 구간에서 수치 모델의 오른쪽과 왼쪽으로 각각 진행하는 지진파 위상이 복잡하게 교차하는 것을 확인할 수 있다. 지진파 간섭 분석의 편의를 위하여 이 분석에서는 수치모의 결과의 수직 성분 속도 기록만을 사용하였다.
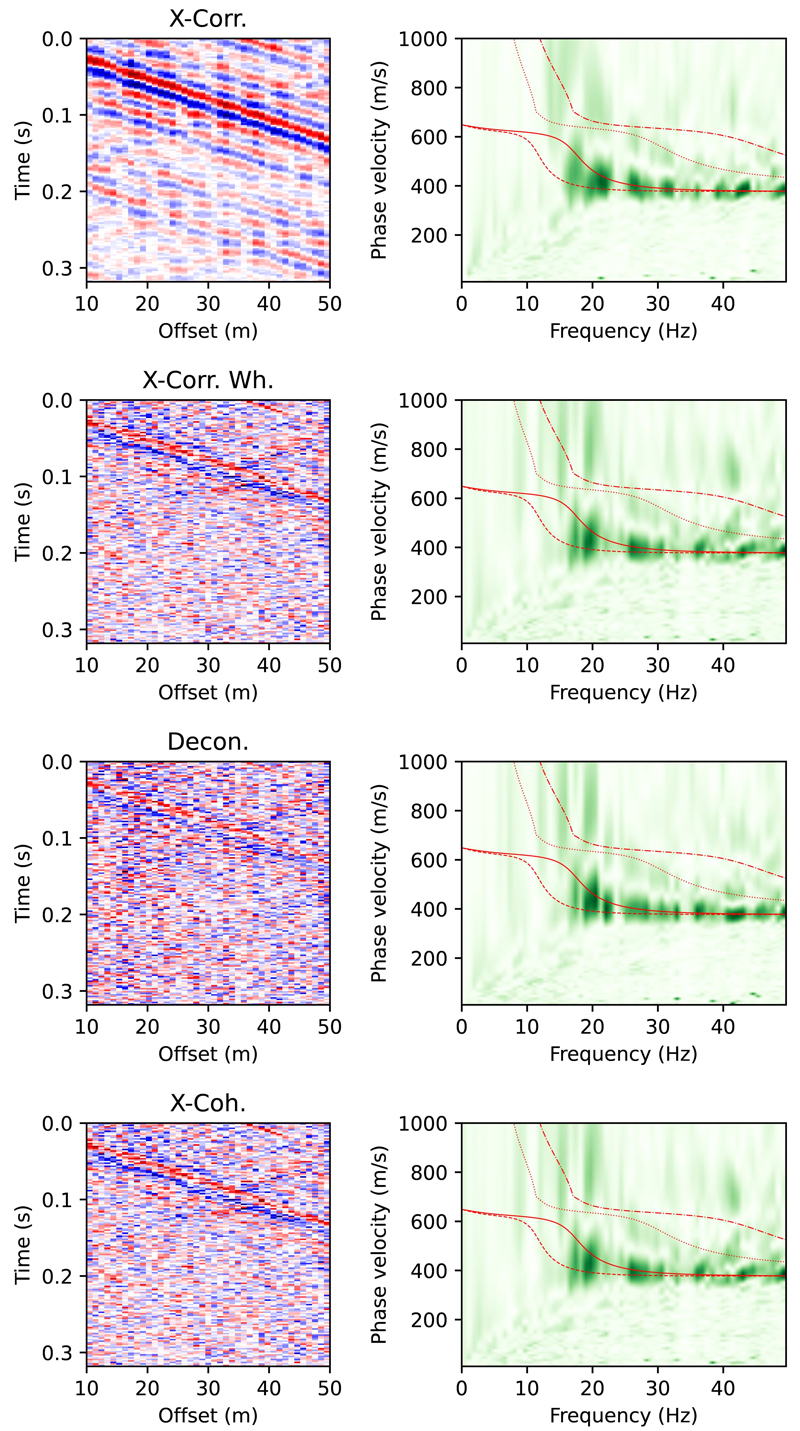
식(2) ~ (5)를 이용하여 그림 3b에서 제시한 교통 잡음 지진기록 단면에 대한 지진파 간섭, 즉 경험 그린함수를 계산하고, 그 결과를 그림 4에 나타냈다. 그림 4의 왼쪽 열은 위로부터 차례로 단순 상호상관(X-Corr.), 초기백색화 상호상관(X-Corr. Wh.), 역합성곱(Decon.), 상호간섭(X-Coh.) 분석 결과를 보여준다. 전체적으로 지진파 간섭의 효과, 즉 표면파의 발달을 효과적으로 추정하고 있음을 확인할 수 있다. 기대한 바와 같이, 초기백색화 상호상관은 단순 상호상관에 비하여 뚜렷한 표면파 추정 결과를 보여준다. 또한 초기백색화 상호상관은 상호간섭 결과와 거의 같은데, 이는 식(3)과 (5)의 비교에서 알 수 있는 바와 같이, 상호간섭에 대한 정규화가 초기백색화의 결과와 같다는 점을 확인해준다. 한편, 역합성곱 결과는 나머지 간섭법에 비하여 관측점 사이의 이격거리(offset)이 증가함에 따라 세로축의 표면파 위상 지연시간이 줄어드는 비물리적인 혼선 현상(crosstalk)이 상대적으로 두드러진다. 이러한 결과는 단순 상호상관과 역합성곱에 대한 분석으로부터 역합성곱의 우세한 결과를 제시하는 Cao et al. (2023)과는 대조적인데, 이는 초기백색화 또는 상호간섭 분석을 그들의 연구에서 포함하지 않은 제한적인 해석으로 여겨진다.
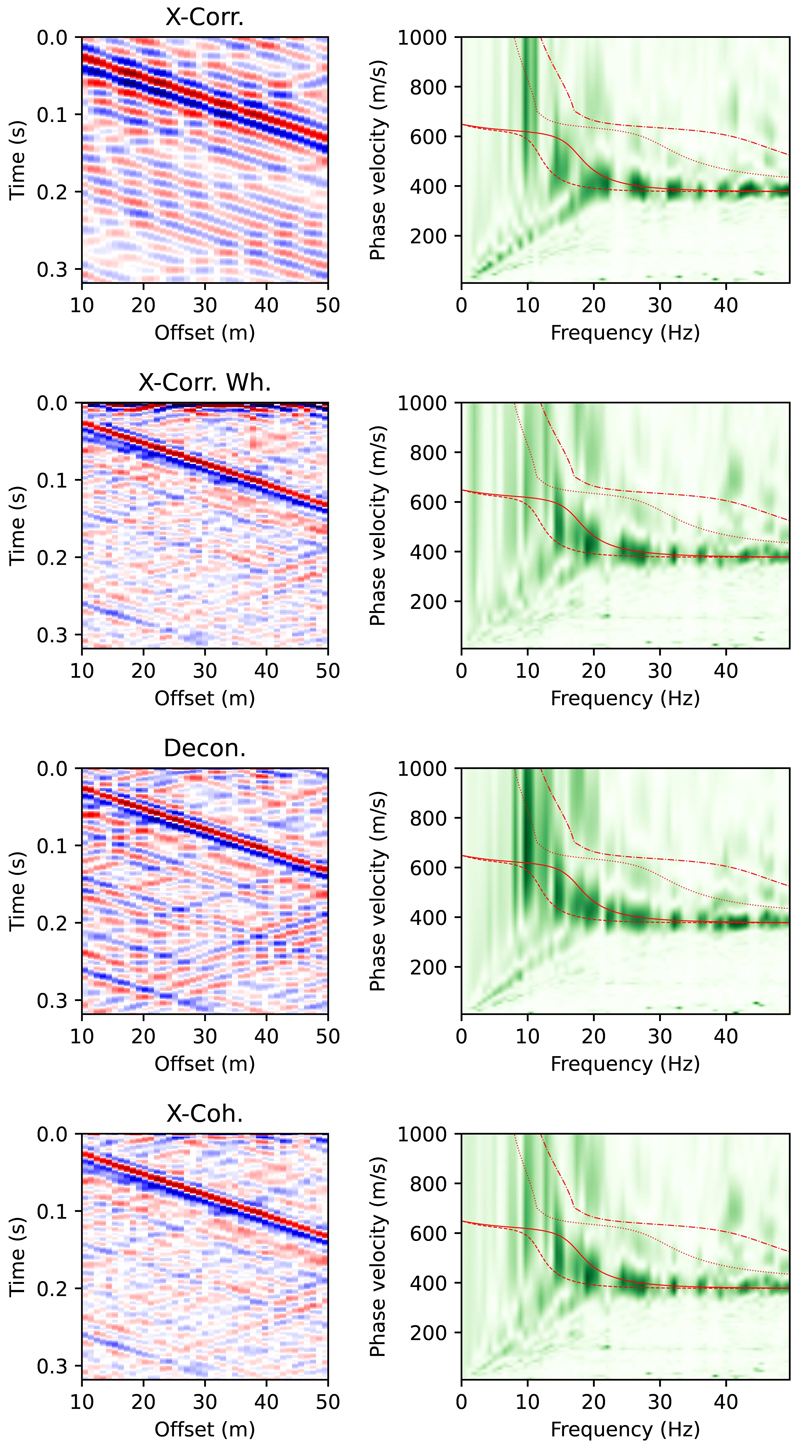
Comparison of seismic interferometries. (Left) Raw cross-correlation, pre-whitened cross-correlation, deconvolution, and cross-coherency interferograms from the top to the bottom; (Right) Corresponding phase velocity dispersion image overlain with theoretical dispersion curves. Solid and dash-dotted lines show the fundamental and first higher modes for a 10-m thick layer and half-space, respectively; dashed and dotted lines show those for a 15-m thick layer and half-space, respectively.
지진파 간섭법을 이용하여 경험 그린함수를 얻는 가장 중요한 목적은 표면파의 분산 특성을 이용하여 전단파 속도구조를 파악하는데 있다. 따라서 앞에서 살펴본 시간영역에서의 표면파 특성이 주파수에 따른 위상속도 변화를 나타내는 분산 곡선 추출을 위한 분해능에 어떻게 반영되는지를 살펴볼 필요가 있다. 분산 분석을 위하여 다중채널 표면파 분석(Multichannel Analysis of Surface Waves; MASW)에서 사용되는 방법을 이용하였다(Park et al., 1998; Ryden et al., 2004). 이 방법에서 위상속도 c와 주파수 f의 함수인 표면파 분산 분포 V(c,f)는 다음과 같은 방정식을 이용하여 구할 수 있다:
| (6) |
여기서 U(x,f)는 지진기록 단면에서 관측점 사이의 이격거리(offset; x)와 시간(t)의 함수인 시계열 u(x,t)의 푸리에 변환 함수이며,k=2πf/c는 파수(wavenumber)이고, R은 관측점의 총 이격거리이다. 실제 계산을 위하여 식(6)에 대한 이산 식은 다음과 같다:
| (7) |
여기서 cm과 fn은 각각 이산 위상속도와 주파수이며, dl은 nx개의 다중채널 관측점 간격 dx로 총 이격거리 R을 이산화한 거리이다. 식(7)을 계산한 결과인 V는 복소수이므로, 분산 분포를 진폭으로 나타내기 위하여 절대값 |V|을 취하였다.
그림 4에 각 지진파 간섭법의 각 경험 그린함수 추출 결과에 대응하는 분산 분포를 함께 제시하였다. 분산 분석 결과는 전반적으로 유사하다. 주파수 10 Hz 이상에서, 수치모델에서 가정한 전단파 속도인 400 m/s와 700 m/s에 상응하는 범위의 표면파 위상 분산 분포를 잘 보여준다. 가장 뚜렷한 분산 진폭 분포는 표면파 분산 곡선의 기본 모드(fundamental mode)에 해당하며, 그 상부에 상대적으로 약하지만 기본 모드와 유사한 변화를 보이는 고차 모드(higher mode)를 확인할 수 있다. 이를 검증하기 위하여, 그림 2a의 수치 모델로부터 지표층의 깊이가 각각 10 m와 15 m인 1차원 층상구조에 대한 기본 모드와 제1차 고차 모드의 이론 분산 곡선을 구하였다. 이론 분산 곡선과 분산 진폭 분포의 중첩 결과는 상호 상관법을 이용하여 얻은 분산 특성을 명확하게 한다. 예상대로, 수치 모델의 중앙부에서 가정한 지표층의 깊이가 10 m에서 15 m 사이로 변화할 때, 분산 분포는 두 깊이의 이론 분산 곡선들 사이에서 가장 큰 진폭을 갖는 지표층 깊이 변화의 평균적인 양상을 나타낸다.
단순 상호상관 분석 결과의 왼편 시간 영역 도시에서는 표면파 위상 지연시간이 다른 허상(artifact)과 혼선(crosstalk)이 두드러져서 다른 간섭 분석 결과에 비하여 품질이 낮은 것으로 보인다. 반면에 분산 분포는 큰 차이가 없다. 주파수 0 - 20 Hz 범위에서 선형적인 분산 분포는 혼선 신호에 의한 것이며, 근소한 차이에도 불구하고 모든 간섭 분석 결과에 공통적으로 나타난다.
자동차 이동에 따른 지진 잡음 연구에서는 크고 작은 자동차 자체의 하중이 지면에 가해지는 다양한 힘의 분포 이외에, 도로의 상태 또는 배경잡음 수준 등과 같이 대상 지역의 여건이나 관측 환경에 따라 다양한 변화를 함께 고려하여야 한다. 이러한 조건들은 관측 기록에 잡음 수준으로 반영된다. 이러한 잡음 수준의 변화에 따라 지진파 간섭법을 적용하고 그 결과를 서로 비교하였다. 그림 3b의 합성 지진기록 단면 자료에 평균(μ) 1을 고정하고 표준편차(σ) 0.2, 0.5, 1.0인 경우에 대하여 가우시안(Gaussian) 분포를 갖는 난수를 곱하여 잡음 상황을 가정하여 재가공한 자료를 산출하였다(그림 5). 이들 자료에 대하여 이전과 동일하게 지진파 간섭법을 적용하였고, 그 결과를 그림 6 - 8에 제시하였다. 가우시안 잡음이 포함되지 않은 자료에 대한 그림 4를 포함하여 그림 6 - 8을 순차적으로 비교하였을 때, 추출된 경험 그린함수는 가우시안 잡음의 표준편차가 커질수록 분해능이 낮아진다. 분산 분석 결과에서 표면파 분산 곡선의 기본 모드와 고차 모드 모두 전반적인 양상에는 큰 차이가 없다. 가장 뚜렷한 변화는 저주파수에서 진폭의 변화 양상이다. 가우시안 잡음의 표준편차가 커질수록, 즉 자동차의 주행에 의하여 발생한 에너지와 외부의 잡음 수준이 유사해질수록, 저주파수 대역에서의 분산 진폭의 분해능이 낮아진다.
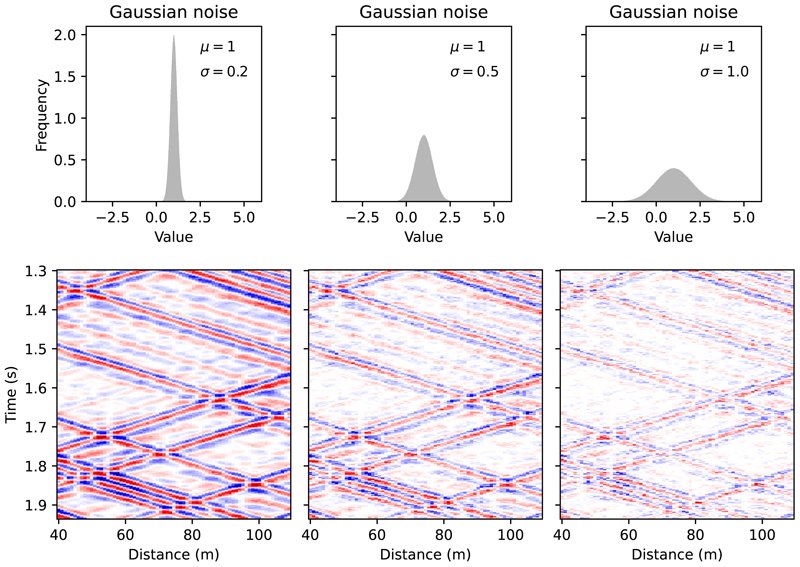
Effect of Gaussian noise on seismic section to mimic the heterogeneous road traffic condition. (Top) Gaussian noise distributions with different standard deviations (σ = 0.2, 0.5, 1.0) and a constant mean (μ = 1); (Bottom) Corresponding seismic section showing the impact of increasing noise levels on wave propagation.
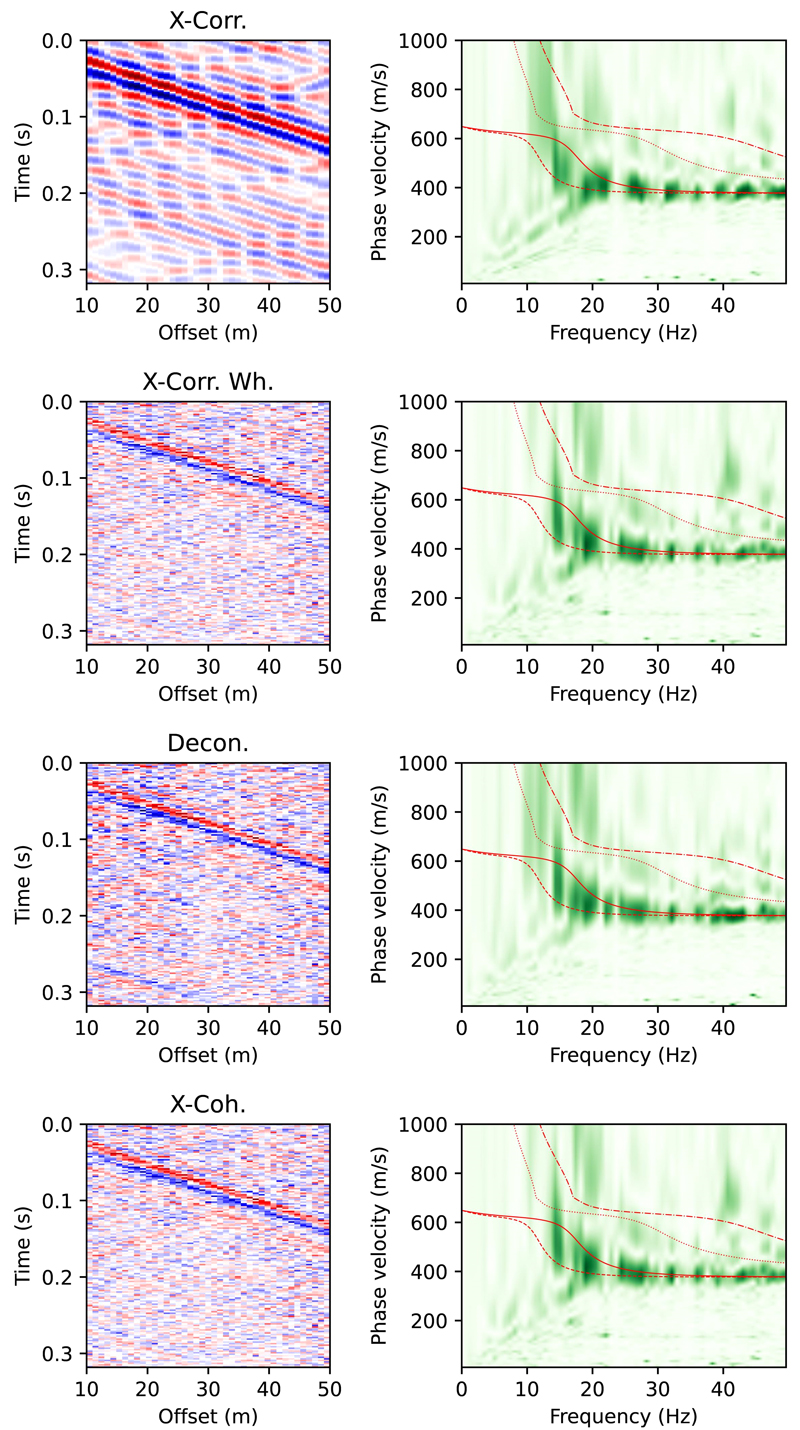
Impact of Gaussian noise (σ = 0.2; left in Fig. 5) on seismic interferometries. Details on each subfigure are as shown in Fig. 4.
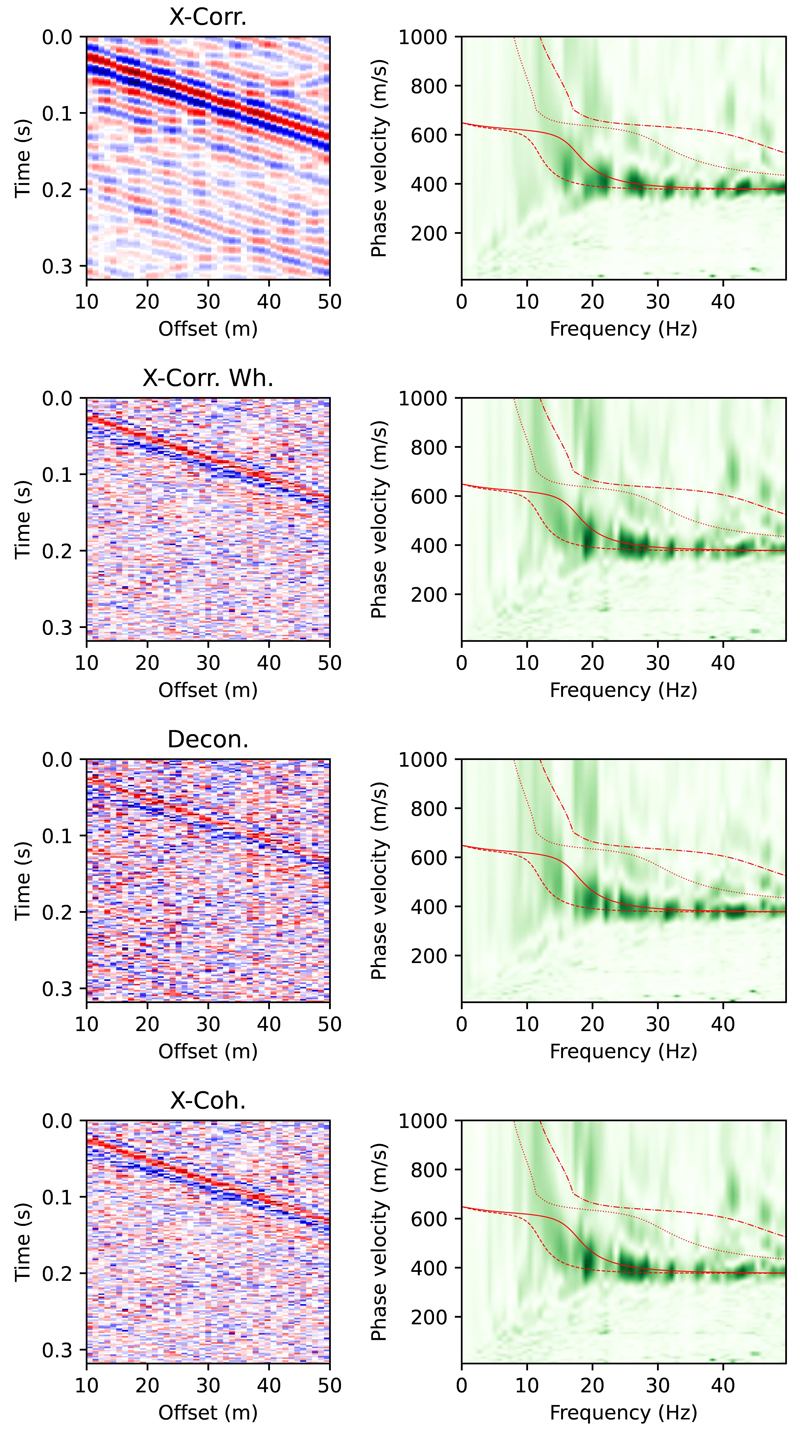
Impact of Gaussian noise (σ = 0.5; middle in Fig. 5) on seismic interferometries. Details on each subfigure are as shown in Fig. 4.
3.2. 야외 관측 실험
실제 도로를 따라 설치한 수진기 배열을 통해 사람의 보행 및 자동차의 주행으로 인하여 발생한 신호를 기록한 지진 자료에 지진파 간섭법을 적용하였다. 국립부경대학교 대연캠퍼스 교내에 있는 한 포장된 직선도로를 따라 도로 중앙으로부터 약 5 m 떨어진 곳에 도로와 나란하게 1 m 간격으로 39개의 지오폰을 설치하였다(그림 9). 나무 등을 피하기 위하여 세 지점에서 지오폰 간격을 기준보다 크게 하였지만, 이러한 경우는 전체의 8% 이하로 균일 간격을 가정한 선형 배열 자료 처리에서 무시하였다. 지오폰은 5 Hz 고유주파수의 SmartSolo IGU-16HR 3C 모델이 사용되었다. 지진기록 취득 샘플 간격은 0.004초(250 Hz)이다. 자료 획득은 2022년 4월 22일에 이루어졌으며, 사람의 보행과 차량의 통행을 확인하기 위하여 영상 촬영을 병행하였다.

Deployment of a geophone array for the field experiment. An aerial view shows the linear arrangement of geophones denoted with red dots spanning about 40 m along a roadway for traffic-induced seismic noise monitoring.
실험 동안 영상을 통하여 확인한 지오폰 배열 주변의 움직임은 직선 도로와 나란한 보도를 따라 양방향으로 이루어진 보행, 소수인 불규칙한 방향의 보행, 직선 도로를 따른 2륜 자전거 및 원동기와 4륜 차량의 주행 등이 있다. 도로는 30 km/h의 주행 제한속력으로 인하여, 전반적으로 차량들은 이 속력 이하에서 주행이 이루어졌다. 또한 실험 구간의 양호하게 포장된 도로에서 차량 이동에 따른 특별한 지면 충격 요인을 확인하기 어렵다. 그림 10은 실험을 통하여 획득한 자료로부터 지진파 간섭법 분석에 사용하기 위하여 추출한 16.504초 동안의 지진기록 단면이다. 전반적으로 도로의 양방향으로 진행한 여러 종류의 움직임이 불규칙하게 섞여 있어서 신호와 특정한 진원의 종류를 구분하기는 어렵다.
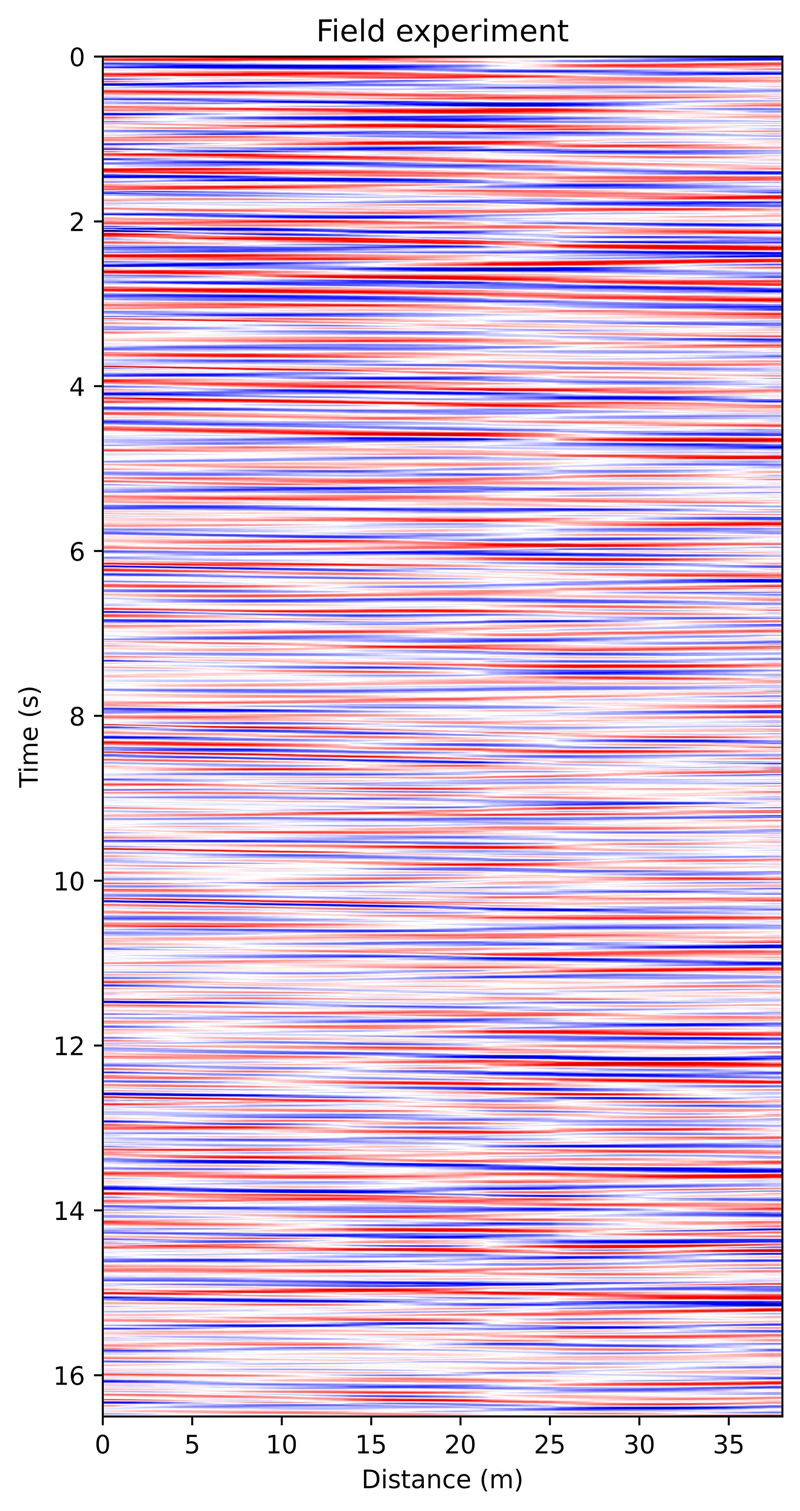
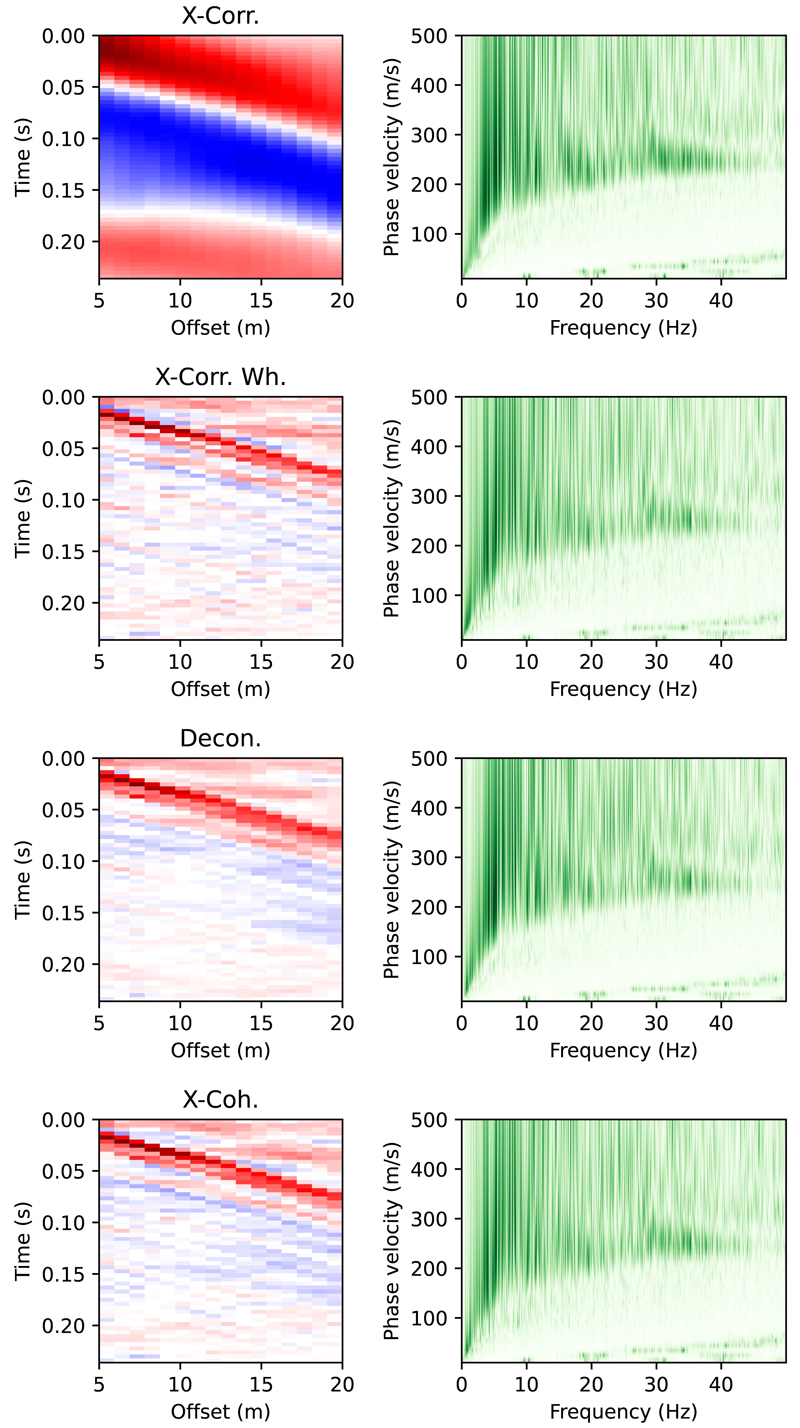
Seismic section from the field experiment. The section illustrates traffic noise from vehicles and pedestrian activity captured by a geophone array deployed along a 40-m roadway segment.
그림 11은 야외 도로 실험으로부터 획득한 자료에 수치모의 자료와 동일한 방식으로 지진파 간섭법을 적용한 결과이다. 모든 간섭법 결과에서 선형적인 위상이 양호하게 발달하고 있지만, 이로부터 표면파 분산 특성을 육안으로 뚜렷하게 파악하기는 어렵다. 대신 분산 분석 결과에서 공통적으로 대략 200 - 300 m/s 범위에 걸쳐서 거의 일정한 위상속도를 확인할 수 있다. 이 결과는 주로 도로를 따라 진행하는 임의의 진원에서 지오폰에 직접 전달된 전단파의 가능성을 암시한다. 실험 지역 하부 지층의 전단파 속도에 대하여 알려진 바는 없다. 다만, 이 지역이 과거 해안 매립으로 형성된 인위적인 지표층을 갖는다는 사실을 감안하여야 한다. 따라서, 국내 지반조사 결과를 종합하여 제안된 지층별 대표 전단파 속도 결과와 비교할 수 있다(매립토층 180 - 240 m/s; Heo and Kwak, 2022). 지진파 간섭법을 적용하여 얻은 위상속도는 기존 매립토층 상부에 다짐이 이루어진 포장 도로 하부 지표층에 대하여 추정할 수 있는 합리적인 결과라고 할 수 있다.
4. 토 의
합성 및 야외 실험 자료에 적용된 지진파 간섭법 가운데, 단순 상호상관은 시간 영역에서 다른 세 방법(초기백색화 상호상관, 역합성곱, 상호간섭)에 비하여 허상과 혼선 현상이 두드러진다. 이와 같은 단순 상호상관의 결과는 직관적인 측면에서 낮은 품질로 이어지는 반면, 분산 분석 결과에서는 큰 차이를 보이지 않는 것이 특징이다. 거리가 증가함에 따라 지연시간이 줄어드는 혼선 현상과 달리, 경험 그린함수의 허상은 전적으로 비물리적인 지연시간에 의한 것으로 위상속도에는 영향을 미치지 않기 때문이다. 역합성곱과 상호간섭은 식(4)와 (5)에서 확인할 수 있는 바와 같이 기본적으로 초기백색화(정규화) 과정을 거치기 때문에, 초기백색화 상호상관과 동등한 결과를 기대할 수 있다. 이 가운데 역합성곱은 계산 과정에서 한 관측점에서의 정보만을 이용하여 결과적으로 두 관측점 모두에 대한 정규화를 수행한다는 점에서 초기백색화 상호상관 및 상호간섭과 차이가 있다.
교통 잡음은 도로 위에 주 에너지원이 제한되어 있으며, 관측점 배열이 도로와 나란하게 배치될 때 주로 도로를 따라 일직선 위에 위치한다. 관측점 선형 배열을 따라 한 방향으로 전파되는 교통 잡음 파장을 상호상관과 역합성곱 및 상호간섭을 계산하여 짧은 시간 동안의 기록을 이용하여도 경험 그린함수를 일관되게 추정할 수 있다. 이 방법은 지진원, 즉 차량의 주행 방향이 선형 관측점 배열과 일치할 때 최적의 성능을 발휘할 수 있다. 그러나 도로가 굽어 있는 경우나 장애물로 인하여 도로와 관측점 배열이 나란하지 않은 경우 등, 교통 잡음 진원과 관측점의 복잡하여 선형 조건이 충족되지 않을 때가 있다. 이러한 경우, 경험 그린함수 추출이 어려워질 수 있다. 교통 잡음 지진기록 자료가 강한 표면파 에너지를 포함하고, 신호대 잡음비가 높을수록 이 연구에서 비교한 네 가지 종류의 지진파 간섭법이 효과적이다. 그러나 이 연구의 야외 실험에서와 같이 직선을 이루는 도로를 주행하는 차량으로 생성된 지진원들로부터 표면파 에너지가 상대적으로 약하거나, 다른 에너지원의 간섭이 심한 경우, 또는 도로 이외의 주변으로부터 잡음이 강한 경우에는 신중한 지진기록 자료의 전처리가 필요할 수 있다. 또한, 이러한 경우에는 안정적인 표면파의 경험 그린함수를 얻기 위하여 더 긴 기록을 사용하여야 한다.
5. 결 론
이 연구에서는 도로를 주행하는 차량이 지면과의 상호작용으로 발생시키는 교통 잡음을 이용하여 표면파를 추출하고 천부 지층의 전단파 속도 구조를 파악하기 위해 네 가지 지진파 간섭법을 비교 분석하였다. 상호상관, 역합성곱, 상호간섭 방법 모두 수에서 십여 초 길이의 짧은 지속시간에 대한 교통 잡음 지진기록으로부터 표면파를 효과적으로 추출할 수 있음을 확인하였다. 초기백색화를 적용한 상호상관법과 상호간섭법이 단순 상호상관법보다 더 명확한 표면파 경험 그린함수 추정 결과를 제공하였다. 역합성곱 방법은 관측점 사이의 이격거리가 증가할수록 비물리적 혼선(crosstalk)이 상대적으로 두드러졌다. 지진파 간섭법을 통해 얻은 분산 곡선은 모두 수치모델에서 설정한 400 m/s와 700 m/s의 전단파 속도에 상응하는 범위의 위상속도를 잘 나타냈다.
분산 분석 결과, 주파수 10 Hz 이상에서 표면파의 기본 모드와 고차 모드를 명확히 확인할 수 있었다. 잡음 수준이 높아질수록 저주파수 대역에서의 분산 진폭의 분해능이 떨어지는 경향을 보였다. 교통 잡음 지진기록이 강한 표면파 에너지를 포함하고 신호대 잡음비가 높을수록, 비교한 네 가지 지진파 간섭법이 효과적임을 확인하였다. 실제 도로에서 수행한 야외 실험으로부터 얻은 교통 잡음 자료에 지진파 간섭법을 적용한 결과, 선형적인 위상이 양호하게 발달했으나 표면파 분산 특성은 육안으로 뚜렷하게 파악하기 어려웠다. 분산 분포도로부터 200 - 300 m/s 범위의 일정한 위상 속도를 확인할 수 있었다. 이는 해안 매립지로 알려진 실험 지역 지표층의 전단파 속도를 적절하게 반영한 결과로 보인다. 이번 연구를 통해 지진파 간섭법을 이용한 교통 잡음 분석이 도시 지역의 천부 지층 전단파 속도 구조를 파악하는 데 효과적임을 확인하였다.
Acknowledgments
이 논문은 부경대학교 자율창의학술연구비(2022년)에 의하여 연구되었다. 야외 실험 자료는 이한별과 함께 캡스톤 프로젝트를 수행한 고혜정, 이은진, 장윤영, 정은수가 획득하였다.
References
- Aki, K., 1957, Space and time spectra of stationary stochastic waves, with special reference to microtremors. Bulletin of the Earthquake Research Institute, The University of Tokyo, 35, 415-456.
-
Behm, M., Leahy, G.M. and Snieder, R., 2014, Retrieval of local surface wave velocities from traffic noise — an example from the La Barge basin (Wyoming). Geophysical Prospecting, 62, 223-243.
[https://doi.org/10.1111/1365-2478.12080]

-
Bensen, G.D., Ritzwoller, M.H., Barmin, M.P., Levshin, A.L., Lin, F., Moschetti, M.P., Shapiro, N.M. and Yang, Y., 2007, Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements. Geophysical Journal International, 169, 1239-1260.
[https://doi.org/10.1111/j.1365-246X.2007.03374.x]

-
Campillo, M. and Paul, A., 2003, Long-range correlations in the diffuse seismic coda. Science, 299, 334-340.
[https://doi.org/10.1126/science.1078551]

-
Cao, W., Huang, X., Hu, Y., Xu, Y., Tang, J. and Yao, H., 2023, Improving surface wave retrieval from traffic noise by deconvolution of the decomposed wavefield. Earth and Space Science, 10, e2022EA002713.
[https://doi.org/10.1029/2022EA002713]

-
Chávez-García, F.J. and Luzón, F., 2005, On the correlation of seismic microtremors. Journal of Geophysical Research, 110, B11313.
[https://doi.org/10.1029/2005JB003671]

-
Cheng, F., Xia, J., Behm, M., Hu, Y. and Pang, J., 2019, Automated data selection in the tau-p domain: Application to passive surface wave imaging. Surveys in Geophysics, 40, 1211-1228.
[https://doi.org/10.1007/s10712-019-09530-2]

-
Heo, G.-S. and Kwak, D.-Y., 2022, Vs prediction model using SPT-N values and soil layers in South Korea. Journal of the Korean Geotechnical Society, 38, 53-66.
[https://doi.org/10.7843/kgs.2022.38.8.53]

-
Kang, T.-S. and Baag, C.-E., 2004a, Finite-difference seismic simulation combining discontinuous grids with locally variable timesteps. Bulletin of the Seismological Society of America, 94, 207-219.
[https://doi.org/10.1785/0120030080]

-
Kang, T.-S. and Baag, C.-E., 2004b, An efficient finite-difference method for simulating 3D seismic response of localized basin structures. Bulletin of the Seismological Society of America, 94, 1690-1705.
[https://doi.org/10.1785/012004016]

-
Kang, T.-S. and Shin, J.S., 2006, Surface-wave tomography from ambient seismic noise of accelerograph networks in southern Korea. Geophysical Research Letters, 33, L17303.
[https://doi.org/10.1029/2006GL027044]

-
Lobkis, O.I. and Weaver, R.L., 2001, On the emergence of the Green’s function in the correlations of a diffuse field. Journal of the Acoustical Society of America, 110, 3011-3017.
[https://doi.org/10.1121/1.1417528]

-
Meier, U., Curtis, A. and Trampert, J., 2007, Global crustal thickness from neural network inversion of surface wave data. Geophysical Journal International, 169, 706-722.
[https://doi.org/10.1111/j.1365-246X.2007.03373.x]

-
Mi, B., Xia, J., Tian, G., Shi, Z., Xing, H., Chang, X., Xi, C., Liu, Y., Ning, L., Dai, T., Pang, J., Chen, X., Zhou, C. and Zhang, H., 2022, Near-surface imaging from traffic-induced surface waves with dense linear arrays: An application in the urban area of Hangzhou, China. Geophysics, 87, B145-B158.
[https://doi.org/10.1190/geo2021-0184.1]

-
Nakata, N., Snieder, R., Tsuji, T., Larner, K. and Matsuoka, T., 2011, Shear wave imaging from traffic noise using seismic interferometry by cross-coherence. Geophysics, 76, SA97-SA106.
[https://doi.org/10.1190/geo2010-0188.1]

-
Park, C.B., Miller, R.D. and Xia, J., 1998, Imaging dispersion curves of surface waves on multi-channel record. SEG Technical Program Expanded Abstracts, 1377-1380.
[https://doi.org/10.1190/1.1820161]

-
Park, C.B., Miller, R.D. and Xia, J., 1999, Multichannel analysis of surface waves (MASW). Geophysics, 64, 800-808.
[https://doi.org/10.1190/1.1444590]

-
Prieto, G.A., Lawrence, J.F. and Beroza, G.C., 2009, Anelastic Earth structure from the coherency of the ambient seismic field. Journal of Geophysical Research: Solid Earth, 114, B07303.
[https://doi.org/10.1029/2008JB006067]

-
Ryden, N., Park, C.B., Ulriksen, P. and Miller, R.D., 2004, Multimodal approach to seismic pavement testing. Journal of Geotechnical and Geoenvironmental Engineering, 130, 636-645.
[https://doi.org/10.1190/1.1820161]

-
Sabra, K.G., Gerstoft, P., Roux, P., Kuperman, W.A. and Fehler, M.C., 2005, Surface wave tomography from microseisms in Southern California. Geophysical Research Letters, 32, L14311.
[https://doi.org/10.1029/2005GL023155]

-
Shao, J., Wang, Y., Zheng, Y., Yao, Y., Wu, S., Yang, Z. and Xue, Q., 2022, Near-surface characterization using urban traffic noise recorded by fiber-optic distributed acoustic sensing. Frontiers of Earth Science, 10, 943424.
[https://doi.org/10.3389/feart.2022.943424]

-
Shapiro, N.M. and Campillo, M., 2004, Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophysical Research Letters, 31, L07614.
[https://doi.org/10.1029/2004gl019491]

-
Shapiro, N.M., Campillo, M., Stehly, L. and Ritzwoller, M.H., 2005, High-resolution surface-wave tomography from ambient seismic noise. Science, 307, 1615-1618.
[https://doi.org/10.1126/science.1108339]

-
Snieder, R., 2004, Extracting the Green’s function from the correlation of coda waves: A derivation based on stationary phase. Physical Review E, 69, 046610.
[https://doi.org/10.1103/PhysRevE.69.046610]

-
Yan, Y., Sun, C., Lin, T., Wang, J., Yang, J. and Wu, D., 2021, Surface-wave simulation for the continuously moving seismic sources. Seismological Research Letters, 92, 2429-2440.
[https://doi.org/10.1785/0220200236]

-
Yao, H., van Der Hilst, R.D. and De Hoop, M.V., 2006, Surface-wave array tomography in SE Tibet from ambient seismic noise and two-station analysis — I. Phase velocity maps. Geophysical Journal International, 166, 732-744.
[https://doi.org/10.1111/j.1365-246X.2006.03028.x]

-
Yokoi, T. and Margaryan, S., 2008, Consistency of the spatial autocorrelation method with seismic interferometry and its consequence. Geophysical Prospecting, 56, 435-451.
[https://doi.org/10.1111/j.1365-2478.2008.00709.x]