한반도 국지지진 규모식의 비교


초록
국내에서 연구되거나 사용 중인 국지지진 규모식의 특성을 파악하기 위하여, 2004년부터 2014년까지 한반도 및 주변 지역에서 발생한 20개 주요 지진의 규모를 결정하고 비교하였다. 지진파의 방사패턴과 전파경로, 부지효과 등의 요인으로 인해 지진계에 기록되는 지진파의 진폭은 매우 가변적이다. 하지만 이러한 변화를 최소화시키며 통계학적으로 안정적인 값이 국지지진규모로 결정되어야 한다. 기상청과 한국지질자원연구원에서 발표한 지진 규모는 다른 규모들과 비교적 큰 표준편차를 보여 통계학적으로 다소 불안정한 것으로 여겨진다. 또한 관측소 규모가 진앙거리와 양의 상관관계를 가지는 계통적인 의존성을 확인할 수 있었다. 국내에서 연구된 규모식들 중에서 Kim and Park (2002)과 Shin et al. (2005)의 연구는 서로 매우 유사한 특성을 가지며, 거리에 따른 계통적인 의존성 또한 낮기 때문에 우리나라의 지진학적 특성을 비교적 잘 반영하는 것으로 나타났다. 하지만, 두 연구에서 사용한 자료 변환 특성의 차이를 감안한다면 우리나라에서 발생하는 지진의 규모를 안정적으로 측정할 수 있는 국지지진규모식 개발을 위한 추가적인 연구가 필요할 것으로 판단된다.
Abstract
Characteristics of local magnitude scales developed and/or used in the Korean Peninsula are compared by measuring the local magnitude scale of major 20 earthquakes occurred in and around the peninsula in the period of 2004 to 2014. Due to the radiation pattern and the propagation path of seismic waves and the site effect, seismic waves recorded at seismometer may have a significant variation in amplitude. However, the size of an earthquake, local magnitude, should be measured in a statistically stable manner by minimizing the variation. It can be thought that relatively large standard deviations among the local magnitude scales show the statistical instability of the magnitudes measured by the Korea meteorological Administration and the Korea Institute of Geoscience and Mineral resources. In addition, it is observed that station magnitudes measured by both institutions are increased with epicentral distance. The local magnitude scales of Kim and Park (2002) and Shin et al. (2005) show similar characteristics to each other, including low distance dependence of station magnitudes. However, considering the difference in deriving the scale between the two approaches, it is believed that further study for the local magnitude scale should be required for the stable measurement of the size of earthquakes occurring around the peninsula.
Keywords:
earthquake, magnitude, local magnitude scale키워드:
지진, 지진규모, 국지지진규모식1. 서 론
지진 규모는 지진의 크기를 측정하기 위해 사용하는 표준적인 단위로, 지진을 구분하거나 분류하기 위한 자연과학적인 관점뿐만 아니라 지진 재해를 최소화하기 위한 지진공학적 관점에서도 중요한 의미를 가진다. 특히 진동이 구조물에 미친 영향이나 인간의 인지 정도, 진앙으로부터의 거리에 따라 크기가 변할 수 있는 진도 계급과 달리 규모는 관측지점의 위치와 무관하게 하나의 값으로 결정되므로, 지진의 크기를 표현하는 기본적인 단위로 사용된다. 그러함에도 불구하고, 지진파의 진폭에 영향을 미치는 다양한 지진학적 요인으로 인해, 본격적으로 지진계가 지진 관측 및 연구에 사용되기 시작한지 수십 년이 지나서야 현대적인 방식의 지진 규모 측정법이 제시되었다(Bäth, 1981).
Richter (1935)는 진앙거리에 따라 지진의 최대 진폭을 도시한 Wadati의 개념에 기반하여 미국 캘리포니아 남부에서 발생한 지진 자료들을 이용한 연구에서 지진의 크기를 측정하는 방법을 제시하고 규모(magnitude)라는 단위를 사용하였다. 그 이후 지진 규모 측정에 관한 연속적인 연구(Gutenberg and Richter, 1956)를 통해 실체파 또는 표면파를 이용해 측정하는 원거리 지진의 규모와 구분하기 위해 국지 지진 규모(local magnitude)라는 용어를 사용하기 시작하였다.
Richter (1935)는 한 지진에 의해 기록된 지진파의 최대 진폭이 진앙 거리가 증가함에 따라 일정하게 감소하며, 여러 지진들의 지진파 최대 진폭이 감소하는 경향이 서로 유사한 특징을 이용해 다음과 같은 대수 함수를 이용해 지진의 크기를 측정하는 방법을 제안하였다.
| (1) |
이 식에서 M 이 지진의 규모이고 A 는 지진계에 기록된 지진파의 최대 진폭이며, - logA0는 거리에 따른 지진파 최대 진폭이 감소하는 경향을 설명하는 기준 곡선으로 거리에 대한 함수로 정의한다. Richter(1935)는 진앙으로부터 100 km 지점에 설치된 Wood-Anderson (WA) 지진계에서 관측한 지진파의 최대 진폭 A 가 1 mm인 지진의 크기가 규모 3.0이 되도록 기준 곡선 - logA0로 정의하였다.
지금은 WA 지진계가 사용되지 않기 때문에, 국지 지진 규모를 측정하기 위해서는 지진계에서 관측한 지진동을 WA 지진계에서 관측한 것처럼 모사하여 최대 진폭을 측정해야 한다. 대부분의 현대식 지진계는 지반 진동에 의해 유도된 전압의 세기를 측정하기 때문에, 이를 지반 진동의 변위 또는 속도와 같은 물리량으로 변환하는 과정을 거쳐야 한다. 이 때 지진계에서 측정한 전압 세기의 변화는 지진계의 고유한 특성인 계기 응답 함수에 의존적이기 때문에, 동일한 장소에 두 지진계가 설치되어 있다하더라도 서로 종류가 다를 경우에는 기록된 지진파형이 일치하지 않을 수 있다. 따라서 각 지진계 고유의 계기응답함수를 제거하여 실제 지반 진동 형태로 변환한 다음 WA 지진계의 기록으로 모사해야 한다.
기준 곡선, - logA0 , 는 지진파가 전파하는 과정에서 발생하는 파동의 기하학적 확산과 비탄성적 감쇠를 고려하기 위한 것이므로 감쇠 곡선 또는 거리 보정항으로 불리며, 대개 지역에 따라 고유한 특성을 가진다. 따라서 각 지역의 지진파 감쇠 특징을 반영한 거리보정항을 사용하는, 지역마다 고유한 지진규모식의 개발이 필요한 것이다.
구조물의 고유 주기는 지진 규모와 더불어 지진재해와 밀접한 관련을 가지는데, 대부분의 구조물들이 가지는 고유 주파수(0.1~1초) 대역에 Richter가 사용한 WA 지진계의 고유 주기(0.8초)가 분포하기 때문에 국지지진 규모는 지진 재해와 직접적으로 관련된다(Bormann, 2002). 따라서 국지지진 규모는 약 6.5~7.0 이상의 큰 규모 지진의 세기를 측정하는 것은 어렵지만(Kanamori, 1983), 지진 공학적으로 매우 중요한 의미를 가지며 지진 재해도 분석에서 가장 기본적인 입력 자료 중 하나로 사용된다.
어떤 지역의 지진학적 특성에 기반한 지진공학적 해석을 위해서는 오랜 기간 관측을 통해 얻어진 지진학적 정보가 필요하기 때문에, 일관된 방식으로 측정된 지진 규모 목록이 필요하다. 우리나라의 경우에는 기상청에서는 1978년부터, 한국지질자원연구원에서는 1994년부터 우리나라를 비롯한 주변지역에서 발생하는 규모 2.0이상의 지진들을 분석하여 국지지진 규모를 발표하고 있지만 기관에 따라 규모의 차이가 있다.
각 기관에서 서로 다른 종류의 국지지진 규모식을 사용하거나 서로 다른 관측소를 분석에 사용했다면 측정한 규모에 차이가 있을 수 있다. 이는 동일한 지진일지라도 지진파의 최대 진폭이 지역적으로 큰 차이가 날 수 있기 때문이다(Boore, 1989). 하지만 최근 국내에서 운영되고 있는 지진관측소의 수가 100개를 넘어섰으며, 각 기관에서 관측한 지진 자료가 실시간으로 공유되고 있는 것을 감안할 때 한반도 및 주변에서 발생한 지진 규모가 0.5 이상 차이가 나거나 서로 불규칙한 관계를 보이는 것은 각 기관에서 사용하는 지진 규모 측정 방식 또는 지진 규모식을 개선해야 할 여지가 있음을 시사한다.
따라서 이 연구는 현재 기상청과 한국지질자원연구원에서 사용하는 지진 규모 측정 방식 및 규모식을 검토하고, 국내 자료를 이용한 국내 기존 연구 결과와 비교하는 것을 주요한 연구 목적으로 하고 있다. 각 기관별 지진 규모 측정 방식 및 규모식은 외부에 자세히 공개되어 있지 않기 때문에, 이 연구를 위해 두 기관에 보낸 동일한 질의서에 대한 응답을 기초로 각 기관의 규모 측정 방식 및 규모식을 비교하였다. 그리고 최근 10여 년 동안 발생한 20개의 주요 지진 규모를 측정하여 그 결과를 비교하였다.
2. 국지지진 규모의 측정
만일 WA 지진계를 사용한다면, 지진 기록에서 읽은 진폭값을 식 (1)에 그대로 대입하면 규모를 측정할 수 있다. 하지만 지금은 이 지진계를 사용하지 않으므로 지진 기록에서 각 지진계 고유의 계기응답함수를 제거한 다음 WA 지진계에서 기록한 것처럼 모사해야 한다.
과거의 연구들에서는 WA 지진계의 제조사에서 제시한 고유주기 0.8초, 감쇠 상수 0.8과 2800의 배율로 표현되는 WA 지진계의 계기응답특성을 사용하였다(Bakun and Lindh, 1977; Kanamori and Jenning, 1978; Kim and Park, 2002). 그런데, 그 동안 알려진 WA 지진계의 배율에 오차가 있기 때문에 2080의 배율과 0.7의 감쇠 상수로 WA 지진계를 모사해야 Richter (1935)의 정의를 따를 수 있는 것으로 알려졌다(Uhrhammer and Collins, 1990). 만일 기존의 배율을 사용해 WA 지진 기록으로 모사하여 지진 규모를 측정하게 된다면, 이론적으로 지진 규모가 약 0.13정도 작게 측정된다(Uhrhammer and Collins, 1990).
지진 기록에서 지진 파형의 최대 진폭을 재는 방식에는 크게 두 가지가 있다. 지진 파형의 세기가 가장 크게 연속적으로 나타나는 골과 마루 사이의 진폭을 잰 다음 0.5를 곱하는 one-half of the peak-to-peak 방식(Gutenberg and Richter, 1956; Hutton and Boore, 1987)과 지진 기록의 평균값(zero)으로부터 가장 큰 진폭의 골 또는 마루까지의 진폭을 사용하는 zero-to-peak 방식(Richter, 1958)이 있다.
Gutenberg and Richter (1956)는 두 수평 성분 최대 진폭의 평균값으로 국지지진 규모를 측정하였으며, Richter (1958)는 수평 성분의 규모를 계산한 다음 규모의 평균을 해당 관측소의 규모로 정의하였다. 전자는 수평 성분 최대 진폭의 산술 평균을 이용한 것이며, 후자는 기하 평균을 이용한 것으로 서로 0.1 정도의 규모 차이가 나타날 수 있다(Bormann, 2002).
수직 성분의 최대값을 이용한 연구들(Greenhalgh and Singh, 1986; Alsaker et al., 1991)에 의하면 이 값이 수평 성분 최대값의 평균과 서로 비슷하기 때문에 지진 규모가 동일하게 측정되는 것으로 알려져 있다(Bormann, 2002).
Richter (1935)는 지진파의 파형(phase)과 무관하게 지진 기록에서 측정한 최대 진폭을 이용하여 규모를 측정하였다. 그런데 Richter (1935)가 사용한 600 km 이내의 거리에서 관측된 최대 진폭은 S파 또는 SH파가 지각 내부에서 반복적인 반사로 인해 발생하는 Lg파이며, 이러한 파형은 지진파의 방사 패턴(radiation pattern)과 전파 경로에 따라 진폭의 변화가 심하게 나타날 수 있다(Ristau et al., 2003). 따라서 지진 규모(network 규모)를 결정할 때 다수의 관측소에서 측정한 지진 규모(station 규모)의 산술평균 보다는 이상치에 의한 영향을 적게 받는 중앙값을 사용하는 것을 선호하기도 한다(Hutton and Boore, 1987; Hutton and Jones, 1993). 또한 단단한 암반에 설치된 관측소들에서도 0.3 정도의 규모 오차가 발생할 수 있는 것으로 알려져 있으며(Boore, 1989), 부지효과에 의해 0.6 정도의 차이가 있을 수도 있으므로(Bakun and Joyner, 1984), 통계학적으로 신뢰할 수 있는 지진 규모를 표현하기 위해서는 관측소 보정항을 사용할 필요가 있다.
가속도계 계기 응답 함수의 주파수 범위가 WA 지진계의 응답 범위를 포함하기 때문에 가속도계 기록을 WA 지진계에 기록된 지진 파형처럼 모사할 수 있고 국지 지진 규모도 측정할 수 있다(Kanamori and Jennings, 1978). 특히 근거리에서 발생한 큰 규모 지진이 속도계 지진계에서는 포화되더라도 가속도계에서는 포화되지 않기 때문에 정확한 최대 진폭을 측정할 수 있다. 또한 관측소별로 측정한 규모의 평균 또는 중앙값을 이용해 지진 규모를 결정하는 것을 고려할 때, 부가적으로 가속도계에서 측정한 규모를 사용함으로써 지진 규모의 통계학적인 신뢰도를 높일 수 있다(Kanamori and Jennings, 1978).
3. 국내 지진 규모식
3.1 기상청의 국지지진 규모
Kim and Park (2002)에 의하면, 기상청에서는 1978년부터 1990년대 중반까지 일본에서 얻어진 다음과 같은 Tsuboi (1954)의 지진 규모식을 사용해 왔다.
| (2) |
이 식에서 Δ는 km 단위의 진앙거리이며, A 는 지진파의 mm 단위의 최대 진폭으로 1978년부터 1990년까지는 수평 성분 최대 진폭의 기하평균을 이용해 지진 규모를 측정하였으나, 이후 1990년말에서 부터는 서울 관측소의 동서 방향의 수평 성분 지진계가 가동되지 않아서 수직 성분 최대 진폭에 를 곱하여 지진 규모를 측정하였다(Kim and Park, 2002).
기상청에서는 1999년에 미국의 Boulder Real Time Technologies 사에서 개발한 Antelope 라는 소프트웨어를 도입하여 현재까지 사용하고 있으며, 미국 서부 캘리포니아에서 사용하는 감쇠식을 일부 수정하여 지진 규모를 결정하는 것으로 알려져 있다(Meteorological Research Institute, 2007). 기상청은 거리에 따른 보정값을 표 형태로 활용하고 있는데, 이를 그림 1에 도시하였다.
지진계에 기록된 신호를 2080의 배율로 WA 지진계의 기록으로 모사한 다음 두 수평성분의 지진 규모를 각각 결정한 후, 큰 값을 station 규모로 사용한다. 그리고 여러 관측소에서 측정한 station 규모들의 중앙값으로 network 규모를 발표한다.
3.2 한국지질자원연구원의 국지지진 규모
한국지질자원연구원은 미국 Science Applications International Corporation 사의 Earthquake Monitoring System을 도입하여 1차적으로 실시간 자동분석을 하고, 이를 기반으로 Analyst Review System을 이용해 지진을 분석한다. 한국지질자원연구원에서는 일본 기상청의 단주기 속도계에 기록된 천부 지진의 최대 진폭을 이용한 Kanbayashi and Ichikawa (1977)와 Takeuchi (1983)의 연구에서 제안한 다음과 같은 규모식을 국내 자료에 맞게 변형하여 규모를 측정하고 있다.
| (3) |
이 식에서 Δ는 km 단위의 진앙거리, α 는 상수 보정항으로 현재 -0.08의 값을 규모 측정에 사용하고 있다(Sheen and Shin, 2010). Vz 는 mkine (10-5 m/sec) 단위를 사용하는 수직성분 속도기록에서 측정한 one-half of the peak-to-peak 최대 진폭을 의미한다. 한국지질자원연구원에서는 지진 파형을 WA 지진계의 기록으로 모사하지 않고, 지진계와 기록계의 민감도로 표현되는 보정상수를 이용해 시간 영역에서 최대 변위 진폭을 측정하여 다음과 같은 식에 대입하여 규모를 측정한다.
| (4) |
이 식에서 Az은 시간 영역에서 측정한 nm 단위의 수직성분 최대 진폭이며, T 는 최대 진폭을 측정한 파형의 주기이다. 이와 같이 관측소별로 station규모를 결정한 다음, 분석자에 의해 선별된 station 규모들의 평균값을 network 규모로 발표한다.
3.3 Hong et al. (2000)의 국지지진 규모
주로 경상분지 일대에 설치된 단주기 지진계에서 1995년 12월부터 1998년 10월 까지 관측한 107개 지진의 지진자료 1054개를 사용하였으며, 사용한 자료의 89%가 진앙거리 200 km 이내에 분포하였다. 수평 성분 관측 자료를 2080의 배율로 WA 지진계의 기록으로 모사하여 최대 진폭을 측정하였다.
지진파가 Richter (1935)의 지진 규모 기준점인 진앙거리 100 km 지점까지 전파하는 과정에서 이미 지역적인 감쇠의 영향을 많이 받을 수 있는데, Hutton and Boore (1987)는 이를 최소화하기 위해 기준 거리와 규모 3.0의 진폭을 각각 17 km, 10 mm로 바꾸어 사용하는 것과 파동의 기하학적 확산과 비탄성적인 감쇠를 설명하는 변수를 독립적인 변수로 구분하여 계산하는 방식을 제안하였다. Hong et al. (2000)은 Hutton and Boore (1987)의 방식을 사용해 기하학적 확산과 비탄성적인 감쇠를 구분하여 계산하였으며, 기준점을 17 km 지점으로 사용하는 규모식을 제안하였다. 그러나 행렬 연산을 하는 과정에서 행렬연산의 안정성 문제로 인해 100 km 지점을 제한방정식(constraint equation)으로 사용하여 규모식을 구한 다음, 17 km를 기준으로 하는 규모식으로 변환하였다. 아래 식에서 R 은 진원거리를 의미한다.
| (5) |
3.4 Kim and Park (2002)의 국지지진 규모
1997년 1월부터 2000년 12월까지 한국지질자원연구원과 기상청의 단주기, 광대역 지진관측소에 기록된 142개 지진의 822개 지진 기록을 이용하였는데 80%정도의 자료가 진원거리 200 km 이내에서 관측된 것이다. 기상청 지진 목록에 있는 46개 지진의 진원 깊이는 10 km 로 고정하였으며, 한국지질자원연구원 목록의 진원 깊이는 발표된 깊이를 그대로 이용하였는데 대부분의 지진은 15 km 이내의 깊이에서 발생한 것으로 보고되었다.
지진 기록은 2800의 배율을 사용해 WA 지진계의 기록으로 모사되었으며, 각 수평 성분의 최대 진폭을 구한 후 기하평균한 값을 최대 진폭으로 사용하였다. 이는 각 수평성분 지진규모의 평균값을 사용한 Righcter (1935)의 정의와 일치한다.
기하학적 확산과 비탄성적 감쇠를 구분하지 않고 하나의 변수로 사용한 Savage and Anderson (1995)와 Kim (1998)의 연구를 바탕으로 국지지진규모식을 개발하였다. 각 지진 기록의 최대 진폭과 진원거리, 100 km 의 기준점에 대한 제한방정식을 이용해 거리 증가에 따른 지진파 최대 진폭의 감쇠 특성을 구한 다음, 캘리포니아 남부와 한반도에서의 3 Hz의 주파수 대역 지진파의 진폭비를 계산하여 한반도의 감쇠 특성을 반영하는 다음과 같은 규모식을 제안하였다.
| (6) |
3.5 Shin et al. (2005)의 국지지진 규모
2000년 1월부터 2004년 5월까지 발생한 125개 지진을 32개 광대역지진관측소에서 기록한 1558개 기록을 이용하여 규모식을 개발하였다. 이 연구는 기하학적 확장과 비탄성적 감쇠를 구분했던 Hong et al. (2000)의 방법과 동일한 방법을 사용하였는데, 2080의 배율을 사용해 WA 지진기록으로 모사하여 수평성분의 최대 변위 진폭과 기준점을 17 km로 사용하는 다음과 같은 규모식을 제안하였다.
| (7) |
3.6 국지지진규모식의 비교
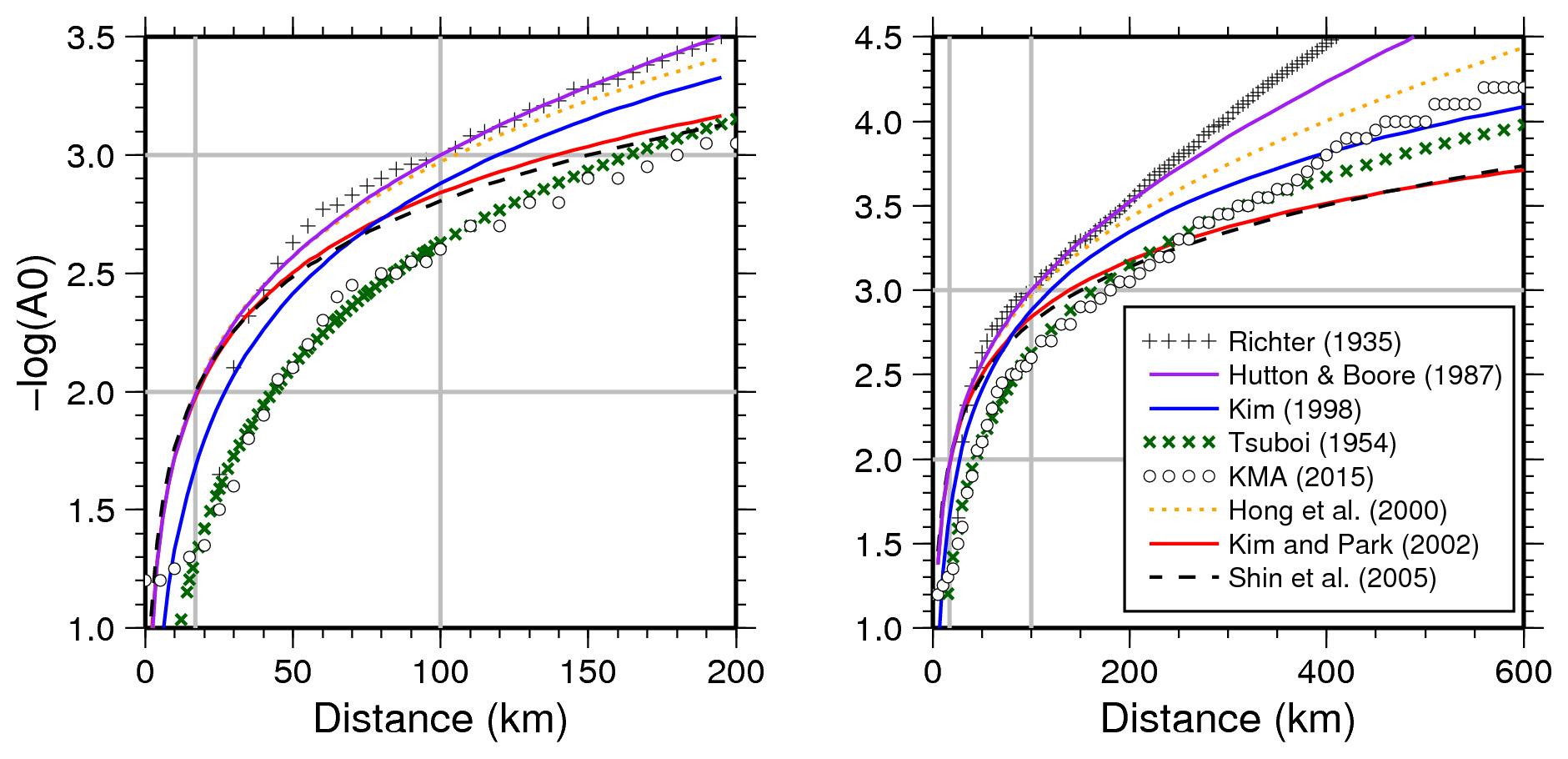
앞서 설명한 국지지진규모식의 거리보정항(- logA0)을 거리에 따라 도시하면 그림 1과 같다. Richter (1935), Tsuboi (1954), Kim (1998)과 기상청, 한국지질자원연구원에서는 진앙거리를 사용하였으며, Hutton and Boore (1987), Hong et al., (2000), Kim and Park (2002), Shin et al. (2005)은 진원거리를 사용하였다. 회색 실선은 17 km와 100 km 지점을 표시한 것으로 Hutton and Boore (1987)에서 설명한 것처럼 각각 10 mm와 1 mm의 최대 변위 진폭을 식 (1)에 대입했을 때, 규모 3.0이 되게 하는 제한 방정식의 조건을 나타낸다.
그림에서 Hutton and Boore (1987)와 Hong et al. (2000)의 거리보정항은 Richter (1935)의 조건을 잘 따르고 있으며, Kim and Park (2002)과 Shin et al. (2005)은 17 km의 기준점에 보정항이 근사되어 있는 것을 알 수 있다. Kim (1998)은 100 km 기준점에 맞춰 거리보정항을 얻은 다음, 캘리포니아 남부와 북미 동부 지역의 감쇠 특성을 고려하여 규모를 보정했기 때문에 제한 방정식의 조건과 일정한 차이를 보인다. 기상청의 규모식은 약 400 km 이하의 거리에서 Tsuboi (1954)와 유사하지만 그 이상의 거리에서는 보정값이 증가하는 것을 알 수 있다. 한국지질 자원연구원의 규모식은 최대 속도 진폭을 기준으로 하기 때문에 함께 비교할 수는 없었다.
Kim and Park (2002)과 Shin et al. (2005)은 각기 다른 배율을 사용해 WA 지진 기록의 최대 진폭으로 변환하여 거리보정항을 얻었지만 서로 매우 유사하게 나타난다. 거리보정항을 기준으로 판단할 때, 기상청은 약 200 km 지점을 중심으로 근거리에서는 Kim and Park (2002)과 Shin et al. (2005)보다 규모를 작게 평가하고 원거리에서는 크게 평가할 것으로 예상된다.
4. 주요 지진의 규모 비교
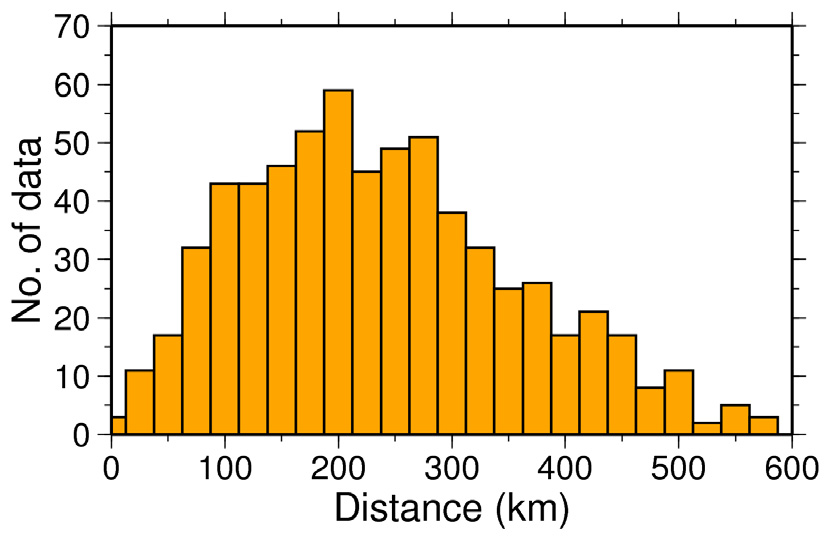
국내 규모식 연구 결과들을 이용해 측정한 지진 규모와 기상청과 한국지질자원연구원에서 측정한 지진규모를 비교하기 위해, 최근 10여 년 동안 발생한 규모 3.0 이상 20개 주요 지진을 표 1과 같이 선정하였다. 이 지진 목록은 기상청 지진 연보를 기준으로 작성하였으며 진앙과 진앙거리 분포는 그림 2, 3에 제시하였다.
두 기관의 홈페이지에서 제공하는 총 692개(×2성분)의 광대역 지진 자료로부터 이상이 있는 자료들은 제거하여, 총 654개의 station 규모를 측정하였다. 지진 기록의 자료처리는 Seismic Analysis Code (Goldstein and Snoke, 2005)를 사용하였다. 자료의 평균(mean)과 선형 기울기(trend)를 없애고 5%의 테이퍼링(tapering)을 적용하여 계기응답함수를 제거하면서 2080의 배율을 가지는 WA 변위계의 기록으로 모사하였다. 두 수평 성분 변위의 zero-to-peak 최대 진폭을 구한 다음, Richter (1958)와 Kim and Park (2002)에서 사용한 수평 성분 최대 진폭의 기하 평균으로 최대 진폭을 결정하였다.
앞서 설명한 국내 지진 규모식 연구에서는 거리 보정항의 계산에 진원거리를 사용하였지만 이 연구에서는 진앙거리를 대입하여 규모를 측정하였다. 만약 10 km의 진원깊이를 가정했을 때 진앙거리 30 km 지점에서 진원거리는 31.6 km 이며, 이로 인한 규모 보정값의 차이는 0.04 정도에 그친다. 게다가 이 연구에서 사용한 자료의 98.8%정도가 진앙거리 30 km 이상인 지점에서 관측한 것이므로, 거리 결정방식의 차이에 기인한 규모 오차는 무시하였다.
수평 성분의 최대 변위 진폭과 진앙거리를 각 규모식들에 대입해 station 규모를 계산하고, 이들의 중앙값으로 각 지진의 network 규모를 결정하였다. 기상청과 한국지질자원연구원에서 발표한 지진 규모와 이 연구에서 결정한 지진 규모를 비교하기 위해 network 규모의 차이를 그림 4에 제시하였다.
KMAc는 기상청 지진 연보에 기술된 규모이며 KMAe는 기상청 거리보정표를 이용해 이 연구에서 측정한 규모이다. KIGAMr은 한국지질자원연구원에서 제공한 지진 규모이다. 한국지질자원연구원에서는 WA 지진기록으로 모사하여 규모를 측정하지 않고 다른 방식으로 규모를 측정하기 때문에 수월한 연구 진행을 위해 이 연구에서는 한국지질자원연구원으로부터 제공받은 station 규모를 그대로 사용하였다. 기상청으로부터도 station 규모 측정값을 제공받았으나 사용한 광대역 관측소의 수가 너무 적었기 때문에, 기상청 규모 측정방식을 따라 재계산한 값(KMAe)을 이용해 비교하였다. Hong, K & P, Shin은 각각 Hong et al. (2000), Kim and Park (2002), Shin et al. (2005)의 거리보정항을 적용하여 결정한 network 규모를 의미한다.
그림 4a는 KMAc 규모와 다른 규모들과의 차이를 도시한 것이고, 그림 4b, 그림 4c는 각각 KMAe 규모, KIGAMr 규모를 기준으로 했을 때 규모 차이를 표현한 것이다. 각 측정방식에 따른 규모 차이의 평균과 표준편차는 표 2에 제시하였다.
KMAc 규모는 다른 규모들과 규모 차이의 표준편차가 약 0.3 정도의 큰 값을 가지는 것으로 분석되었으며 기상청 거리보정표를 이용해 재계산한 KMAe규모는 국내 지진 규모식 연구 결과를 이용한 규모들과 약 0.1 정도의 작은 표준편차를 보였다. KIGAMr규모는 KMAc 규모를 제외한 다른 규모들과 0.2 이내의 표준편차가 있는 것으로 분석되었는데, 이러한 표준편차의 차이는 network 규모 결정에 사용한 관측소의 수에 기인한 것으로 판단된다. 기상청과 한국지질자원연구원에서 제공한 자료들에 의하면, 기상청에서는 평균적으로 6개의 관측소, 한국지질자원연구원에서는 16개의 관측소를 사용한 반면에 이 연구에서는 평균적으로 33개의 관측소를 사용해 각 지진의 network 규모를 결정하였다. 따라서 두 기관에서 발표하는 지진 규모가 지진파의 방사패턴이나 전파 경로에 따른 진폭 변화를 잘 감안하는, 통계학적으로 치우침이 없는 규모라고 판단하기는 어렵다.
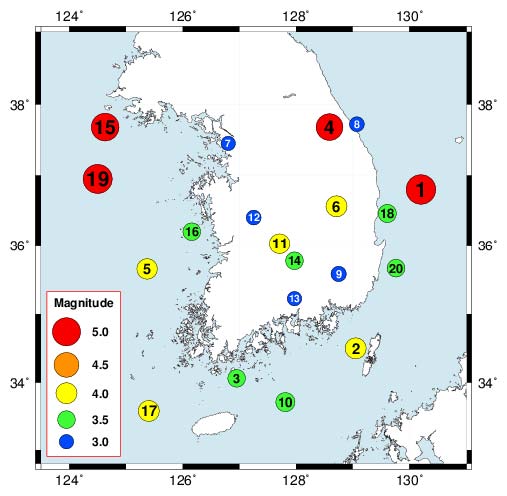
Location map of epicenters of the events used in this study. Numbers in circles represent the event number given in Table 1.
Hong et al. (2000)의 규모는 다른 연구 결과에 비해 평균적으로 규모가 0.3 정도 크게 측정되었으며, Kim and Park (2002)과 Shin et al. (2005)은 서로 규모 차이가 거의 없는 것으로 확인된다. 이는 그림 1을 통해 쉽게 예측할 수 있는데, Hong et al. (2000)의 거리보정항은 다른 국내 연구 결과들에 비해 보정값이 크며, Kim and Park (2002)과 Shin et al. (2005)은 서로 비슷한 거리보정항을 가지고 있기 때문이다. 그런데 기상청에서 사용하는 거리보정항이 Kim and Park (2002), Shin et al. (2005)과 뚜렷한 차이를 보이는데도 불구하고, KMAe 규모는 이들의 규모와 0.1 이내의 작은 차이를 보인다. 이것은 기상청에서 사용하는 거리보정항이 이들의 거리보정항과 200 km를 기준으로 서로 엇갈리고 있는데, 이 연구에서 사용한 약 58%의 자료가 진앙거리 200 km 이상에서 관측한 것이기 때문으로 해석할 수 있다. 즉 KMAe 규모가 근거리에서 작게 측정하고 원거리에서 크게 측정한 것이 서로 상쇄되어 규모 차이를 줄인 것으로 판단된다.
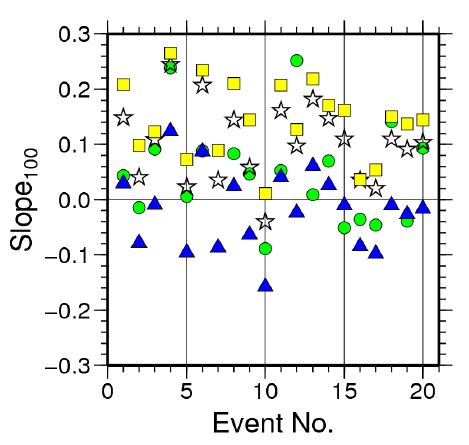
이를 뒷받침하는 KMAe 규모의 거리 종속적 특성은 그림 5에서 쉽게 관찰할 수 있다. 각 지진의 station규모를 진앙거리에 대한 1차 함수로 가정하여, 각 지진마다, 각각의 식으로 측정한 station 지진 규모와 진앙거리와의 상관관계를 조사하였다. 회귀분석을 통해 얻은 1차 함수의 기울기에 100을 곱한 결과를 도시한 것이며, 100 km 마다 station 규모가 얼마나 증가 또는 감소하는지를 나타낸다. 이 그림에서 사용한 기호는 그림 4에서 사용한 기호와 동일한 의미를 가지는데, 대체로 기상청(KMAe)과 Hong et al. (2000)은 station 규모가 거리와 양의 상관관계를 가지는 것으로 해석할 수 있다.
이 연구에서 사용한 20개 지진에 대한 거리 종속적 특성의 평균값으로 판단한다면, 100 km 마다 KMAe는 0.14, Hong et al. (2000)은 0.10씩 station 규모가 증가하는 경향을 가지며, KIGAMr은 0.08씩 커지고, Kim and Park (2002)과 Shin et al. (2005)은 0.02씩 규모가 감소한다. 따라서 Kim and Park (2002)과 Shin et al. (2005)의 거리보정항이 우리나라의 지진학적 특성을 비교적 잘 반영하고 있는 것으로 해석된다.

Mean and standard deviation of magnitude differences corresponding to the distance correction curves.
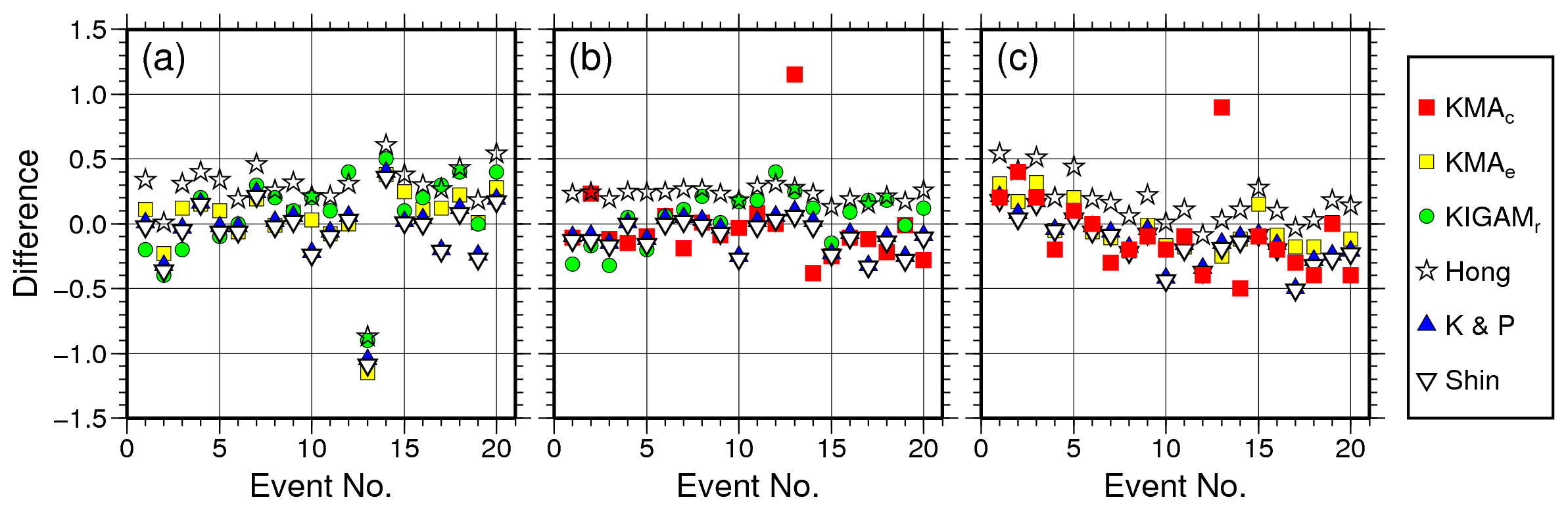
Comparison of differences of network magnitudes corresponding to the distance correction curves. The reference magnitudes of (a), (b), and (c) are the catalog magnitude of the KMA (KMAc), the network magnitude obtained from the distance correction table of the KMA (KMAe), and the network magnitude from the KIGAM report (KIGAMr), respectively. Star, blue triangle, and inverted triangle represent the network magnitude obtained from the distance correction curve of Hong et al. (2000), Kim and Park (2002), and Shin et al. (2005), respectively.
5. 토의 및 결론
이 연구에서는 현재 우리나라 기상청과 한국지질자원연구원에서 사용하는 지진 규모 측정 방식과 규모식을 검토하고, 국내 자료를 이용한 국내 기존 연구 결과와 비교하였다. 이를 위해 최근 10여 년 동안 발생한 20개의 주요 지진 규모를 측정하여, 각 규모식에 의해 결정된 지진 규모를 비교하였다.
충분히 많은 지진을 사용해 분석한 것은 아니지만, 기상청과 한국지질자원연구원의 지진 규모가 통계학적으로 다소 불안정한 것으로 나타났는데, 가장 큰 이유는 규모 측정에 충분하지 못한 수의 자료만 사용했기 때문인 것으로 사료된다. 국지지진규모 측정에 사용되는 S파나 Lg파는 지진파의 방사패턴과 전파경로, 부지효과의 영향을 많이 받기 때문에, 지진 규모 측정에 다수의 관측 자료를 사용하고, 관측소 보정항을 적용하는 것이 필요할 것이다. 또한 station규모가 진앙 거리와 양의 상관관계를 가지는 계통적인 의존성을 보이므로 한반도의 지각특성을 반영한 규모식의 개발과 적용이 필요한 것으로 여겨진다.
Kim and Park (2002)과 Shin et al. (2005)의 거리 보정항은 서로 매우 유사한 특성을 가지며, 거리에 따른 계통적인 의존성 또한 낮기 때문에 우리나라의 지진학적 특성을 비교적 잘 반영하는 것으로 판단된다. 하지만 Kim and Park (2002)은 2800의 배율을 가진 WA 지진계로 모사한 최대 진폭으로부터 도출된 것인데 비해, Shin et al. (2005)은 2080의 배율로 모사한 진폭을 사용한 것을 감안한다면 측정된 규모는 서로 0.13 정도의 차이를 보인다 할 수 있다.
지진 규모식은 다수의 지진 기록을 이용해 해당 지역의 지진학적 특성을 잘 반영할 수 있도록 개발되어야 한다. 지진 기록이 충분하지 못한 영국과 같은 지역에서는 최근에서야 축적된 다수의 지진 기록을 바탕으로 고유의 지진 규모식을 개발하기도 하였으며(Ottemöller and Sargeant, 2013), 지진이 빈번히 발생하여 지진 기록이 충분한 판 경계 지역에서도 꾸준한 연구를 통해 규모식을 통합하고 개선하고 있다(Uhrhammer et al., 2011). 특히 우리나라 기상청과 동일한 Tsuboi (1954)의 규모식을 사용하던 일본 기상청에서도 거리에 따른 지진 규모의 계통적인 차이를 발견하고, 2003년 9월 25일 지진 규모식을 개정한 것은 주목할 만하다(Katsumata, 2004). 따라서 우리나라에서도 추가적인 연구를 통해 국지지진 규모식의 체계적인 개발과 적용이 이루어져야 할 것으로 판단된다.
Acknowledgments
이 연구는 기상청 기상지진기술개발사업(CATER 2014-5050)의 지원으로 수행되었습니다.
References
- Alsaker, A., Kvamme, L.B., Hansen, R.A., Dahle, A., and Bungum, H., (1991), The ML scale in Norway, Bulletin of the Seismological Society of America, 81, p379-389.
- Bakun, W.H., and Joyner, W.B., (1984), The ML scale in central California, Bulletin of the Seismological Society of America, 74, p1827-1843.
- Bakun, W.H., and Lindh, A.G., (1977), Local magnitudes, seismic moments, and coda durations for earthquakes near Oroville, California, Bulletin of the Seismological Society of America, 67, p615-629.
-
Bäth, M., (1981), Earthquake magnitude - Recent research and current trends, Earth-Science Reviews, 17, p315-398.
[https://doi.org/10.1016/0012-8252(81)90014-3]

-
Boore, D.M., (1989), The Richter scale: its development and use for determining earthquake source parameters, Tectonophysics, 166, p1-14.
[https://doi.org/10.1016/0040-1951(89)90200-X]

- Bormann, P., (2002), Magnitude of seismic events, in IASPEI New Manual of Seismological Observatory Practice, Bormann, P. ed., Potsdam: GeoForschungsZentrum, ISBN 3-9808780-0-7.
- Goldstein, P., and Snoke, A., (2005), http://ds.iris.edu/ds/newsletter/vol7/no1/sac-availability-for-the-iriscommunity// (June 5, 2015).
- Greenhalgh, S.A., and Singh, R., (1986), A revised magnitude scale for South Australian earthquakes, Bulletin of the Seismological Society of America, 76, p757-769.
- Gutenberg, B., and Richter, C.F., (1956), Earthquake magnitude, intensity, energy, and acceleration: (Second paper), Bulletin of the Seismological Society of America, 46, p105-145.
- Hong, T.G., Baag, C.E., and Shin, J.S., (2000), The ML scale in southern Korea, Journal of the geological society of Korea, 36, p545-558, (in Korean with English abstract).
- Hutton, L.K., and Boore, D.M., (1987), The ML scale in southern California, Bulletin of the Seismological Society of America, 77, p2074-2094.
- Hutton, L.K., and Jones, L.M., (1993), Local magnitudes and apparent variations in seismicity rates in Southern California, Bulletin of the Seismological Society of America, 83, p313-329.
-
Kanamori, H., (1983), Magnitude scale and quantification of earthquakes, Tectonophysics, p185-199.
[https://doi.org/10.1016/0040-1951(83)90273-1]

- Kanamori, H., and Jennings, P.C., (1978), Determination of local magnitude, ML, from strong-motion accelerograms, Bulletin of the Seismological Society of America, 68, p471-485.
- Kanbayashi, Y., and Ichikawa, M., (1977), A method for determining magnitude of shallow earthquakes occurring in and near Japan, Quarterly Journal of Seismology, 41, p57-61, (in Japanese with English abstract).
- Katsumata, A., (2004), Revision of the JMA displacement magnitude, Quarterly Journal of Seismology, 67, p1-10, (in Japanese with English abstract).
- Kim, S.K., and Park, M.A., (2002), The local magnitude scale in the Korean Peninsula, Journal of the geological society of Korea, 38, p217-235, (in Korean with English abstract).
- Kim, W.Y., (1998), The ML scale in eastern north America, Bulletin of the Seismological Society of America, 88, p935-951.
- Meteorological Research Institute, (2007), Development of local magnitude, Korea Meteorological Administration, p213.
-
Ottemöller, L., and Sargeant, S., (2013), A local magnitude scale ML for the United Kingdom, Bulletin of the Seismological Society of America, 103, p2884-2893.
[https://doi.org/10.1785/0120130085]

- Richter, C.F., (1935), An instrumental earthquake magnitude scale, Bulletin of the Seismological Society of America, 25, p1-32.
- Richter, C.F., (1958), Elementary Seismology, W.H. Freeman and Co., San Francisco, California, p578.
-
Ristau, J., Rogers, G.C., and Cassidy, J.F., (2003), Moment magnitude - local magnitude calibration for earthquakes off Canada's west coast, Bulletin of the Seismological Society of America, 93, p2296-2300.
[https://doi.org/10.1785/0120030035]

- Savage, M.K., and Anderson, J.G., (1995), A local-magnitude scale, Bulletin of the Seismological Society of America, 85, p1236-1243.
- Sheen, D.-H., and Shin, J.S., (2010), Earthquake detection thresholds of broadband seismic networks in South Korea considering background seismic noise levels, Journal of the Geological Society of Korea, 46, p31-38, (in Korean with English abstract).
- Shin, J.S., Chi, H.C., and Cho, C.-S., (2005), Review on ML scales in Southern Korea, Journal of the Korean Geophysical Society, 8, p207-209, (in Korean with English abstract).
- Takeuchi, H., (1983), Magnitude determination of small shallow earthquakes with JMA electromagnetic seismograph Model 76, Quarterly Journal of Seismology, 47, p112-116, (in Japanese with English abstract).
- Tsuboi, C., (1954), Determination of the Gutenberg-Richter’s magnitude of earthquakes occurring in and near Japan, Zisin, 7, p185-193, (in Japanese with English abstract).
- Uhrhammer, R.A., and Collins, E.R., (1990), Synthesis of Wood-Anderson seismograms from broadband digital records, Bulletin of the Seismological Society of America, 80, p702-716.
-
Uhrhammer, R.A., Hellweg, M., Hutton, K., Lombard, P., Walters, A.W., Hauksson, E., and Oppenheimer, D., (2011), California integrated seismic network (CISN) local magnitude determination in California and vicinity, Bulletin of the Seismological Society of America, 101, p2685-2693.
[https://doi.org/10.1785/0120100106]