백두산의 폭발적인 분화시 발생가능한 화쇄류의 영향 범위에 대한 VolcFlow 수치 모의

1. 서 론

백두산은 북한과 중국의 국경 지역에 위치하며, 경위도의 범위는 북위 41°41'~42°51', 동경 127°43'~128°16'이다. 행정구역상으로는 북한 양강도 삼지연군과 중국 길림성 연변조선족자치주에 속한다. 백두산은 이 곳에서 시작되어 금강산, 설악산을 거쳐 소백산, 지리산으로 이어지는 한반도의 산맥의 줄기인 이른바 백두대간의 시작지점이며, 또한 남만주에서 서남서 방향으로 발달한 장백산맥의 주봉이다. 2,500 m 이상의 여러 봉우리가 천지를 둘러싼 칼데라 외륜산으로 존재하며, 최고봉인 장군봉(將軍峰)의 높이는 2,750 m로 한반도에서 가장 높은 산이다. 이 외륜산을 이루고 있는 산봉우리들은 다량의 알칼리 계열의 규장질 용암과 화성쇄설암으로 구성되어 있다(Yun and Cui, 1996)

백두산은 대략 3단계의 화산활동으로 만들어진 화산으로, 제 1단계는 신생대 올리고세(약 28.4 Ma)이후에 선캄브리아 시대의 변성암류와 중생대 화산암과 화강암을 기반암으로 하는 대륙열곡(틈새)을 따라 틈새 분출한 현무암질 화산활동을 시작하여 용암대지를 형성하였고, 플라이오세(4.4~1.7 Ma)에 점차 화산활동의 중심이 천지 쪽으로 옮겨감에 따라 중심 분출로 순상화산체를 형성하였다. 그 후 약간의 휴식기를 거친 후, 제4기 플라이스토세 말기인 60만 년 전(0.6 Ma) 다시 제 2단계 화산활동이 재개되어 1만 년 전까지 조면암 용암과 화성쇄설암이 교호로 분출하는 화산활동을 통하여 백두산 복합화산체(성층화산)를 형성하였으며, 제 3단계로 홀로세인 약 4천 년 전(4 ka)과 약 1천 년 전(1 ka) 조면암질 내지 알칼리유문암질 부석을 위주로 하는 대폭발이 발생하여 성층화산 산정부가 폭발하고 함몰하여 천지 칼데라를 형성한 화산활동으로 구분할 수 있다(Yun et al., 1993, 2007; Wei et al., 2007).

대략 946년 경(Xu et al., 2013), 밀레니엄 분화(Millennium Eruption)라고 하는 중심 분화에 의하여 직경 5 km의 칼데라가 형성되었다. 천지는 칼데라 내부에 물이 고여서 형성된 칼데라호이다. 천지의 수면은 해발 고도가 2,189 m이고, 남북 길이 4.4 km, 동서 길이 3.37 km에 달하며, 둘레는 약 13.1 km, 호수 면적은 9.82 km², 평균 깊이는 213 m, 최대 수심은 373 m에 이르며, 천지 내에 들어있는 물의 양은 약 20억 톤에 달한다(Yun et al., 2014)

밀레니엄 분화는 화산폭발지수(VEI) 7에 해당하는 초거대 분화(Soh and Yun, 1999)로, 이로 인해 발생한 강하 부석층의 흔적은 일본 홋카이도와 혼슈 북부지역에서 1~5 cm 층후로 발견된 백두산-토마코마이 테프라(B-Tm: Baegdusan-Tomakomai tephra)로부터 시작하여 백두산 방향으로 갈수록 점점 두꺼워져서, 동해 해저에서 10 cm 내외, 그리고 백두산 부근에서는 최대 층후가 73 m에 달한다(Machida et al., 1981, 1990; Machida and Arai, 1983; Horn and Schmincke, 2000; Guo et al., 2006; Wei et al., 2013; Yun and Koh, 2014).

Fig. 1.

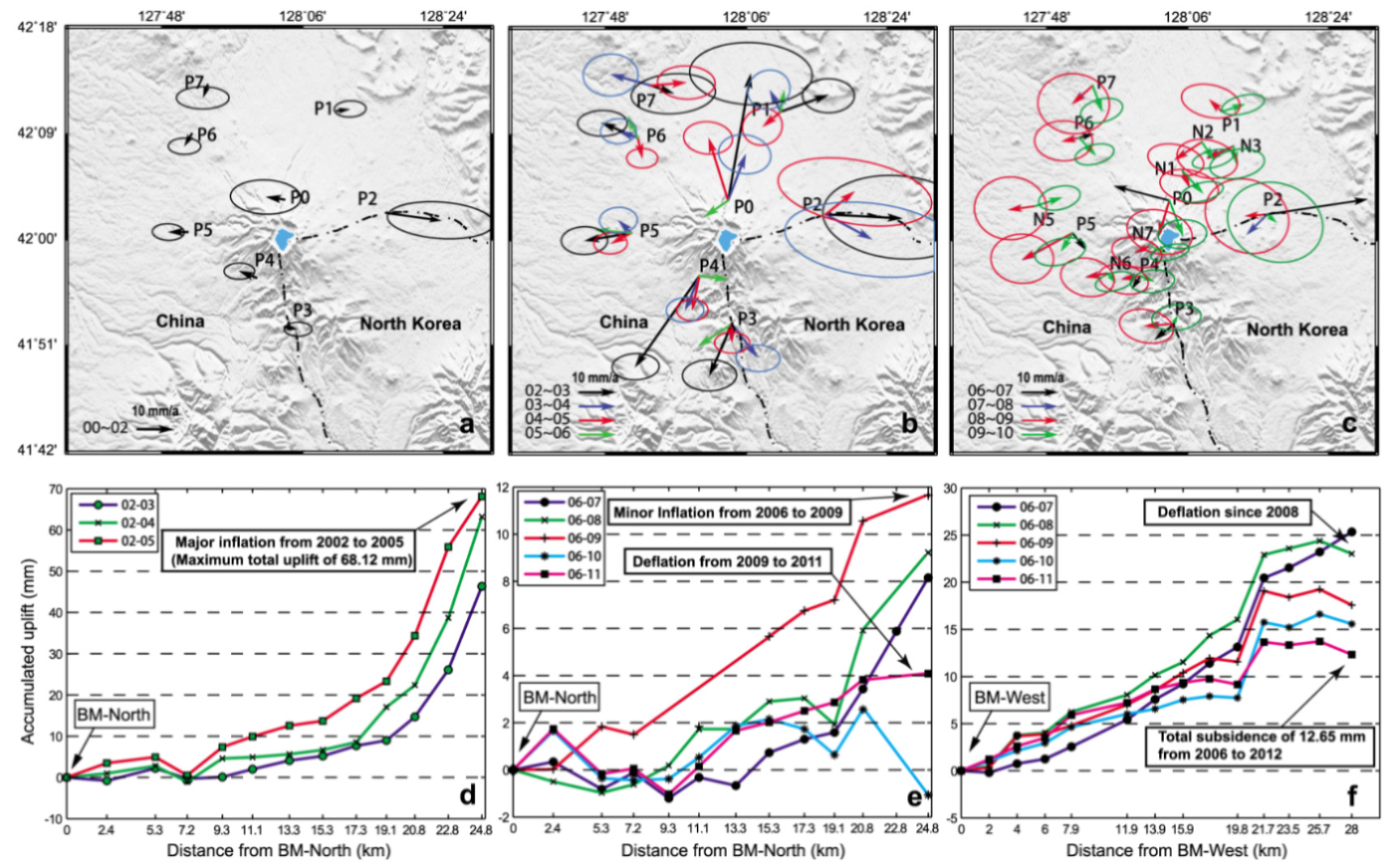
Surface deformation from GPS and precision leveling survey. GPS horizontal displacements with 95% confidence ellipses of (a) 2000-2002, inactive period; (b) 2002-2006, active period with inflation; and (c) 2006-2010, inactive period. Vertical displacements along the precision leveling routes for the periods of (d) 2002-2005 on the north slope, (e) 2006-2011 on the north slope, and (f) 2006-2011 on the west slope. The horizontal axis in d-f represents the distance between the survey site and the reference site (Xu et al., 2012).

천지의 물은 승차하(乘搓河)라고 불리는 칼데라 외륜산 북쪽의 가장 낮은 계곡으로 흘러나가면서 68 m의 비룡폭포(장백폭포)에서 떨어져 이도백하(二道白河) 및 송화강(松花江)의 발원지가 된다. 또한 남쪽 산정에서 압록강이, 동쪽 무두봉(無頭峰) 북쪽에서 두만강이 발원한다.

백두산에 대한 역사시대 분화 기록에 대한 연구자료(Yun and Cui, 1996; Miyamoto et al., 2010; Yun and Lee, 2011; Yun, 2013)에 의하면 백두산에서는 역사시대 중에 서기 939년의 분화로부터 1925년의 수증기 분화까지 지속적으로 분화활동이 일어났다. 일본기략, 고려사, 고려사세가, 동국문헌비고, 조선왕조실록, 승정원일기, 장백산강강지략 등으로부터 파악된 백두산의 역사시대 분화 기록은 약 30여 차례 이상이며, 가장 최근에는 약 100년 전인 1903년의 수증기마그마 및 1925년에 소규모의 수증기 분화가 있었다(Simkin and Siebert, 1994; Yun and Cui, 1996; Wei et al., 2002; Yun and Lee, 2011; Yun, 2013).

또한, 백두산 천지 일원에서는 2002년에서 2005년까지 지하 마그마의 관입에 의한 화산성 지진이 급증하고 지표면의 비정상적인 변형이 발생하였다(Wu et al., 2007; Liu et al., 2011; Xu et al., 2012; Yun and Lee, 2012). 2002년도부터 2009년도까지 GPS관측을 통하여 지표면의 수평 변위를 측정한 결과, 2002년 이후 천지 칼데라 정상부를 중심으로 화산체의 팽창이 나타났으며(Cui et al., 2007; Xu et al., 2012), 2002년~2003년도에 약 4.6 cm의 팽창을 보였고 그 이후 감소하는 경향이 나타났다. 백두산 산사면의 정밀 수준 측량 결과 2009년까지 최대 10 cm 이상의 수직 팽창이 나타났다(그림 1). 2006년도 이후 수평 및 수직 변화율은 감소하는 추세이나 여전히 불안정한 상태이다.

이 외에도 온천에서 채취한 화산가스를 분석한 결과 헬륨 동위원소비(³He/⁴He)의 값이 6 정도로 높게 나타났으며, 이것은 맨틀 물질의 상승으로 인한 것으로 해석되었다(Shangguan and Sun, 1997; Gao, 2007). 그리고 천지 주변의 온천수의 온도가 69℃에서 점진적으로 증가하여 최대 83℃로 상승하였으며, 화산가스에 의하여 고사목이 관찰되었고, 화산성 지진으로 인한 수차례의 산사태 및 암벽붕괴도 발생하였다. 이러한 화산성 불안정(volcanic unrest)의 징후는 백두산이 잠재적으로 분화 가능성이 있다는 것을 지시하는 것이다(Yun and Lee, 2012).

지난 2000년 동안 화산재해로 인한 인명 피해 중 가장 높은 비율을 차지하는 것은 화쇄류(pyroclastic flow; 화성쇄설밀도류, pyroclastic density currents)이다(Auker et al., 2013). 화쇄류가 발생하게 되면 인명, 재산, 기간시설 등에 영구적인 위협을 가하게 된다(Yun et al., 2013). 백두산에서 플리니안 분화로 인한 화쇄류가 발생할 경우, 화산폭발지수 6 내지 7 이상일 경우 인구 60만 명의 이도백하진(鎭)을 포함한 중국의 여러 도시와 북한의 혜산시(惠山市), 삼지연시(三池淵市) 등이 그 영향권에 들어가며(Yun et al., 2013), 이들 지역에는 수백만 명의 인명이 거주하고 있으므로 백두산에서 대규모의 분화가 발생할 경우 많은 인명과 재산 피해가 발생할 가능성이 있다.

따라서 백두산에서 발생 가능한 화쇄류의 피해범위를 알아내어 화쇄류로 인한 피해를 최소한으로 줄이기 위해 화쇄류의 거동을 모의하고자 하였다. 컴퓨터를 통한 수치모의가 시작된 이래로, 다양한 재난을 모의하기 위하여 실제의 모습에 잘 들어맞도록 다양한 변수를 사용하는 프로그램들이 개발되어 왔으며, 이중 다양한 화산재해를 모의하기 위한 프로그램들 중에는 탄도비행하는 화성쇄설물의 궤도를 계산하는 Eject! (Mastin, 2001), 라하르, 화성쇄설밀도류 등 다양한 종류의 집단류를 계산할 수 있는 VolcFlow (Kelfoun and Druitt, 2005; Kelfoun et al., 2008; 2009; Davies et al., 2010)나 Flow3D (Sheridan et al., 2000), Titan2D (Sheridan et al., 2005; Procter et al., 2010; Sulpizio et al., 2010), 용암류를 계산하기 위한 FLOWGO (Harris and Rowland, 2001), 라하르를 계산하기 위한 LaharZ (Schilling, 1998; Muñoz et al., 2009; Vargas et al., 2010)가 있다. 또한 강하화산재를 예측하기 위한 HAZMAP (Macedonio et al., 2005), ASHFALL (Hurst, 1994), TEPHRA와 TEPHRA 2 (Bonadonna et al., 2005; Bonadonna, 2006; Connor, 2006) 등이 있다(Constantinescu et al., 2011).

본 연구에서는 백두산에서 폭발적 분화가 발생했을 때 발생 가능한 화쇄류의 도달 거리를 모의하기 위하여 위와 같은 여러 수치 시뮬레이션 모델 중 VolcFlow 모델을 적용하여 수치 시뮬레이션을 실행하였다.

2. 연구방법

2.1 VolcFlow 모델

VolcFlow는 프랑스 Clermont-Ferrand의 Laboratoire Magmas et Volcans (2015) 소속 Dr. Karim Kelfoun에 의해 개발된, 고밀도의 등온 화산성 흐름을 수치 시뮬레이션하는 프로그램이며, 화산재해의 피해 범위를 예측하기 위하여 세계 각국에서 사용하고 있다. 홈페이지의 프로그램 소개(http://lmv.univ-bpclermont.fr/volcflow/)에 의하면, VolcFlow는 다음과 같은 영역에서 사용된다.

• ① 화쇄류, 암설사태 및 다른 지구물리학적 집단류의 유동학적 거동을 파악한다.
• ② 집단류의 지표면상에서의 흐름을 시각화하고, 이것이 지표면 상의 구조에 어떤 영향을 받는지를 비교하거나 해석한다.
• ③ 결과를 바탕으로 화산재해의 재해위험도(圖)를 작성하는 데 활용한다.

VolcFlow 수치 시뮬레이션 모델은 깊이에 대한 지형 내에서의 평균 근사값(depth-average approximation)에 기초하여, 특정지역의 지표면과 평행한 x와 y성분, 그리고 그것과 수직인 h를 사용하는 좌표계와 연계된 수치지형을 사용한다(Kelfoun and Drutt, 2005; Kelfoun et al., 2008; 그림 2). 방정식은 이중 풍상 오일러 차분법(a double upwind Eulerian scheme)에 기초한 충격-수집(shock-capturing) 수치해석 방법을 사용하여 해석된다(Kelfoun and Druitt, 2005). 이 방식은 충격, 소파(rarefaction waves), 그리고 입자 튕김(granular jumps)을 처리 가능하고, 복잡한 지형과 수치적으로 ‘젖은’ 그리고 ‘마른’ 표면 모두에서도 안정적으로 적용 가능하다(Kelfoun and Druitt, 2005; Kelfoun et al., 2008). VolcFlow 모델은 마찰(층저 및 내부 마찰각), 빙햄, 점성, 보엘미 등 다양한 유동학에 대하여 적용 가능하며, 또한 사용자에 의한 더욱 복잡한 유동학적 법칙의 정의가 가능하다(Kelfoun et al., 2008).

Kelfoun and Druitt (2005)에 따르면, 오일러 풍상차분법은 셀의 중앙에서 두께 h와 지면표고 z같은 스칼라항의 값을 정하고 계산하며, 셀의 가장자리에서는 플럭스 Φ와 속도 u = (u,υ)같은 벡터항의 값을 계산한다. 흐름의 두께 평균값($$ \overline{h}$$)은 셀 가장자리에서, 속도의 평균값 $$ \overline{\text{u}}=\left(\overline{u},\overline{v}\right)$$은 셀 중앙에서 계산된다(그림 3). 셀의 가장자리(i - 1/2,j)에서는 먼저 보존방정식의 근원항을 계산하고, 그 후 이류항을 계산한다.

VolcFlow는 칠레의 Socompa산의 암설사태(Kelfoun and Druitt, 2005; Kelfoun et al., 2008), 에콰도르의 Tungurahua화산의 화쇄류(Kelfoun et al., 2009), Reunion 섬의 사면붕괴로 인한 쓰나미(Kelfoun et al., 2010) 등의 수치모의에 사용되었다.

Fig. 2.

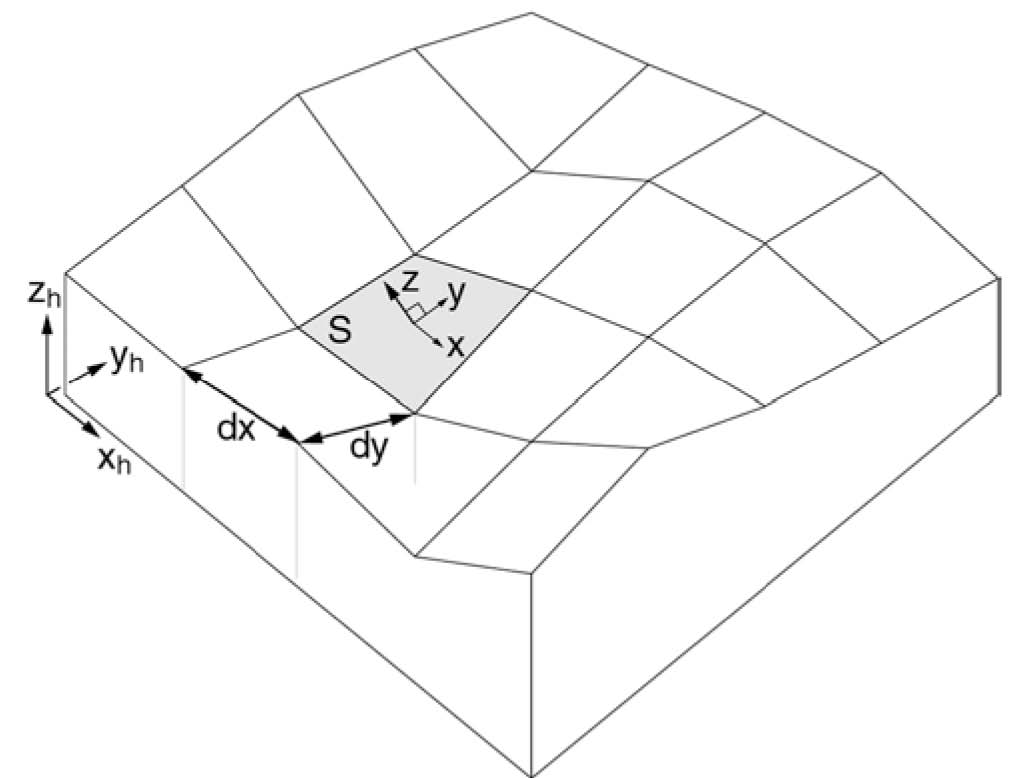
Geometry of the calculation domain. The ground topography is defined using horizontal axes xh and yh, and vertical axis zh (Kelfoun and Druitt, 2005).

Fig. 3.

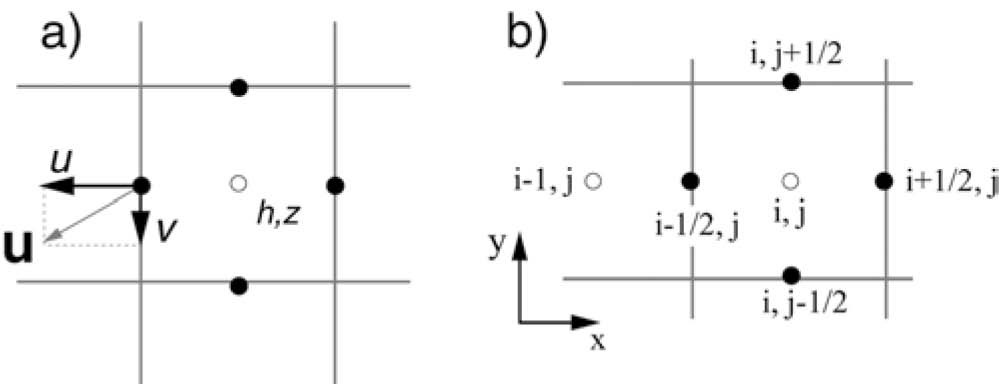
Definitions of (a) scalars, vectors, and (b) cell notation in the numerical scheme (Kelfoun and Druitt, 2005).

Table 1.

The parameters using simulations according to the Volcanic Explosivity Index (VEI).

2.2 VolcFlow를 이용한 화쇄류 시뮬레이션

백두산에서 폭발적인 분화에 의해 발생할 수 있는 화쇄류를 모의하기 위하여, 역사시대 분화기록에 대한 분석 결과, 대부분이 화산재가 분화하여 함경도 지역으로 확산된 강하화산재가 주류를 이루었으며, 이는 백두산의 근대 분화가 플리니안 분화를 위주로 하였음을 지시한다(Yun, 2013; Yun et al., 2014). 따라서 먼저 백두산 천지 칼데라 내부에서 폭발적인 분화가 발생한다고 가정하였다. 이 때, 분화로 인하여 형성된 분연주가 중력에 의해 붕괴하여 화쇄류가 발생하는 것(Branney and Kokelaar, 2002)으로 가정하고, 이를 사실적으로 모의하기 위하여 VolcFlow의 개발자 Dr. Karim Kelfoun의 조언을 구하였다.

그 결과 분연주 붕괴에 대한 가장 현실적인 모의방법은 화구 상부의 지형을 원뿔 형태로 수정하는 것이었으며, 따라서 천지 칼데라 상부에 임의의 원뿔 형상을 가정하고 화쇄류가 중력에 의해 붕괴하며 그 원뿔의 사면을 타고 흘러내리도록 모의하도록 결정하였다. 그러나 관련된 선행 연구 자료는 부족하므로, 가정하는 원뿔의 규모는 직접 설정하였다.

2.2.1 화산폭발지수에 따른 원뿔의 규모

분화의 규모에 따라 원뿔의 규모 역시 조정하는 것이 좋다는 개발자의 조언에 따라, 화산폭발지수에 따라 천지 칼데라 상부에 가정한 원뿔의 높이와 밑면의 반지름을 달리 설정하였다. 화산폭발지수 3일 경우에는 원뿔의 밑면의 반지름을 2,000 m, 원뿔의 높이를 1,000 m로 설정하였으며, 화산폭발지수 4일 경우에는 원뿔의 밑면의 반지름을 2,500 m, 원뿔의 높이를 1,250 m로 설정하였고, 화산폭발지수 5일 경우에는 원뿔의 밑면의 반지름을 3,000 m, 원뿔의 높이를 1,500 m로, 화산폭발지수 6일 경우에는 원뿔의 밑면의 반지름을 4,000 m, 원뿔의 높이를 2,000 m로, 화산폭발지수 7일 경우에는 원뿔의 밑면의 반지름을 5,000 m, 원뿔의 높이를 3,000 m로 설정하였다.

2.2.2 붕괴 분연주의 부피

각각의 화산폭발지수별로 방출되는 물질의 총 부피 중 10%가 화쇄류로 형성됨을 가정하여 분출물의 부피를 정하였다. 화산폭발지수 3일 때는 화쇄류의 부피를 10⁶ m³ 로, 화산폭발지수 4일 때는 화쇄류의 부피를 10⁷ m³ 로, 화산폭발지수 5일 때는 화쇄류의 부피를 10⁸ m³ , 화산폭발지수 6일 때는 화쇄류의 부피를 10⁹ m³ 로, 화산폭발지수 7일 때는 화쇄류의 부피를 10¹⁰ m³ 로 정하였다.

2.2.3 층저마찰각과 내부마찰각

화쇄류의 물리적인 거동을 가정하기 위한 내부마찰각은 Kelfoun의 조언을 구하였고, 변수에는 흐름의 내부 상태에 대한 다른 변수가 포함되어 있으므로, 0° 로 설정하라는 조언을 얻었다. 층저마찰각은 흐름의 온도와 입자의 밀도와 같은 흐름 내부의 조건뿐만 아니라 흐름과 접하는 지표면의 기복이나 피복 상태에 따라서도 달라지는데, 시뮬레이션을 위하여 3°, 5°, 10°로 각각 정하여 다양한 상황을 모의하였다.

2.2.4 항복응력, 밀도, 점도

Rowley (2010)에 따르면, 화성쇄설밀도류의 항복응력은 2,000 Pa에서 100,000 Pa까지 나타나고, 입자의 밀도는 500에서 3,000 kg · m^-3, 점성도는 1.78×10^-5 Pa · s로 나타난다고 하였다. 따라서 각각의 층저마찰각에 대한 항복응력을 각각 5,000, 10,000, 15,000 Pa로 설정하여 비교하였다. 그 외에 입자의 밀도는 2,000 kg · m^-3으로, 점도는 1×10^-5 Pa · s로 설정하였다.

Table 2.

Simulated range of pyroclastic density currents according to the volcanic explosivity index (VEI), eruption volume, simulated cone radius and height, basal friction angle, and cohesion at the Mt. Baekdu.

2.2.5 분화지속시간과 시뮬레이션 시간

화산폭발지수에 따른 분화의 특성(Newhall and Self, 1982)에 따라, 화산폭발지수 3일 경우에 분화의 지속시간을 3,600 초(1시간), 총 모의시간을 7,200 초(2시간), 화산폭발지수 4와 5에서는 분화의 지속시간을 21,600 초(6시간), 총 모의시간을 43,200 초(12시간), 화산폭발지수 6과 7에서는 분화의 지속시간을 43,200 초(12시간), 총 모의시간을 86,400 초(24 시간)로 설정하였다(표 1). 모의시간을 분화시간보다 길게 설정한 것은 분화가 끝난 이후에도 화쇄류가 계속 확산되는 것을 시뮬레이션하기 위해서이다.

종합하면, 5단계의 화산폭발지수에 대하여 3단계의 층저마찰각을 정하고 다시 3단계의 항복응력을 설정하여 총 45개의 시나리오를 설정하였다. 분화위치의 중심, 즉 원뿔의 중심은 천지 칼데라 중심이고, UTM좌표로 421963, 4651169이다.

3. 시뮬레이션 결과

설정된 45개의 시나리오에 대한 수치 모의를 실시하여, 분화구 중심으로부터 최대로 도달한 거리를 측정하였다(표 2).

화산폭발지수 3의 경우, 화쇄류가 천지 칼데라 내부를 채우지만 천지 칼데라 외륜산 밖으로 흘러넘치지는 않았다. 화쇄류가 천지 칼데라 밖으로 넘치지 않았으므로 각각의 변수에 대한 거리 차이는 거의 없었다. 화쇄류가 분화구 중심으로부터 최대로 도달하는 거리는 약 2.3 km이다.

화산폭발지수 4의 경우, 화쇄류가 천지 칼데라 내부를 채우고 흘러넘쳤다. 흘러넘친 화쇄류의 대부분은 외륜산의 가장 낮은 곳인 북쪽 승차하 계곡 방향으로 흘러넘치고 일부는 서쪽의 계곡으로 흘러넘쳤다. 층저마찰각이 3°이고 항복응력이 5,000 Pa일 때, 분화구 중심으로부터 화쇄류가 최대로 도달하는 거리는 9.1 km이다. 3°, 10,000 Pa일 때 7.2 km, 3°, 15,000 Pa일 때 6.7 km, 5°, 5,000 Pa일 때 6.9 km, 5°, 10,000 Pa일 때 6.3 km, 5°, 15,000 Pa일 때 6.0 km, 10°, 5,000 Pa일 때 5.3 km, 10°, 10,000 Pa일 때 4.8 km, 10°, 15,000 Pa일 때 4.1 km까지 도달하였다.

화산폭발지수 5의 경우, 화쇄류가 천지 칼데라 내부를 채우고 흘러넘쳐 주로 외륜산의 가장 낮은 곳인 북쪽 승차하 계곡 방향과 북동쪽, 서쪽 및 남서쪽의 계곡으로 멀리 흘러넘쳤다. 층저마찰각이 3°이고 항복응력이 5,000 Pa일 때, 분화구 중심으로부터 화쇄류가 최대로 도달하는 거리는 14.4 km이다. 3°, 10,000 Pa일 때 13.4 km, 3°, 15,000 Pa일 때 13.0 km, 5°, 5,000 Pa일 때 10.7 km, 5°, 10,000 Pa일 때 9.4 km, 5°, 15,000 Pa일 때 9.1 km, 10°, 5,000 Pa일 때 6.7 km, 10°, 10,000 Pa일 때 6.4 km, 10°, 15,000 Pa일 때 6.2 km까지 도달하였다.

화산폭발지수 6의 경우, 분연주 붕괴의 모의를 위해 천지 칼데라 상부에 가정한 원뿔의 규모가 천지 칼데라보다 크기 때문에, 화쇄류는 칼데라 외륜산을 넘어 전방위로 확산되었다. 층저마찰각이 3°이고 항복응력이 5,000 Pa일 때, 분화구 중심으로부터 화쇄류가 최대로 도달하는 거리는 18.6 km이다. 3°, 10,000 Pa일 때 17.4 km, 3°, 15,000 Pa일 때 17.1 km, 5°, 5,000 Pa일 때 13.1 km, 5°, 10,000 Pa일 때 12.7 km, 5°, 15,000 Pa일 때 12.4 km, 10°, 5,000 Pa 일 때 8.8 km, 10°, 10,000 Pa일 때 8.6 km, 10°, 15,000 Pa일 때 8.1 km까지 도달하였다.

화산폭발지수 7의 경우, 분연주 붕괴의 모의를 위해 천지 칼데라 상부에 가정한 원뿔의 규모가 천지 칼데라보다 크기 때문에, 화쇄류는 칼데라 외륜산을 넘어 전방위로 확산되었다. 층저마찰각이 3°이고 항복응력이 5,000 Pa일 때, 분화구 중심으로부터 화쇄류가 최대로 도달하는 거리는 23.4 km이다. 3°, 10,000 Pa일 때 21.7 km, 3°, 15,000 Pa일 때 20.9 km, 5°, 5,000 Pa일 때 17.8 km, 5°, 10,000 Pa일 때 17.4 km, 5°, 15,000 Pa일 때 17.4 km, 10°, 5,000 Pa 일 때 12.4 km, 10°, 10,000 Pa일 때 12.4 km, 10°, 15,000 Pa일 때 12.3 km까지 도달하였다.

4. 토 의

백두산에서 발생 가능한 화쇄류의 도달 범위에 대한 수치모의에 대한 연구는 Yun et al. (2013, 2014)에서 TITAN2D 모델을 사용하여 이루어진 적이 있다.

TITAN2D 모델을 통한 백두산에서 발생 가능한 화쇄류의 모의(Yun et al., 2014)에서는 화쇄류의 최대 도달 거리를 모의할 때 화쇄류의 층후가 0.1 m (10 cm)로 퇴적되는 곳까지를 기준으로 하여 화쇄류 뿐아니라 화쇄난류에 의해 조금이라도 영향을 줄 수 있는 범위를 산출하였다. 본 연구에서의 VolcFlow 모델을 이용한 수치모의에서는 화쇄류의 최대 도달거리의 기준을 층후 1 m 퇴적 기준으로 선택하여 모의하였다. 또한 본 연구에서는 화쇄류의 부피를 분출물의 총 부피의 10%까지만 모의했으므로, TITAN2D 모델을 통한 모의에서 분출물의 총 부피의 20~30%로 설정했을 때 도출된 최대 도달 거리와 직접적인 비교를 하기는 힘들다. 따라서 각 화산폭발지수에서 총 분출물의 부피 중 화쇄류로 형성되는 비율을 조절하여 시뮬레이션을 추가로 실시하는 등의 보완 연구가 필요하다고 판단된다.

VolcFlow 모델을 이용한 수치모의에서 동일한 화산폭발지수와 항복응력을 설정하고 내부마찰각만을 다르게 한 것을 비교하였을 경우, 내부마찰각이 감소할수록 도달 범위가 증가하여, 화산폭발지수 4의 경우에서는 3.8 km 정도 더 멀리 도달하며 화산폭발지수 7의 경우에는 최대 11 km 정도 더 멀리 도달하였음을 알 수 있다. 이것은 Yun et al. (2013)가 TITAN2D를 통한 연구결과에서 밝힌, 다른 조건은 동일하고 층저마찰각을 25°와 16°로 설정하였을 경우에 층저마찰각이 작은 쪽에서 화쇄류가 더 멀리 도달한다는 결과와 일치한다. 다만 각각의 모의에서 설정한 층저마찰각의 크기가 큰 차이가 나는 이유는, TITAN2D모델의 입력 변수에서 입자류의 속도를 감속시킬 수 있는, 즉 진행방향과 반대 방향의 가속도가 작용하도록 만드는 변수는 두 종류의 마찰각만이 존재하지만, VolcFlow모델의 경우에는 항복응력 및 밀도, 점도의 작용을 고려하므로, 이를 감안하여 VolcFlow에서는 고려하는 층저마찰각의 크기는 TITAN2D의 경우보다 충분히 낮게 설정해야 한다고 판단된다. 각각의 화산폭발지수에 대하여 항복응력이 동일하고 층저마찰각이 3°, 5°, 10°로 변화할 때의 화쇄류에 의한 피해 범위의 시각적인 결과를 비교하였다(그림 4).

Fig. 4.

Comparison of different basal friction angle. With the same VEI and yield stress (these are in case of 5,000 Pa). Runout range of PDCs are increase in inverse proportion to basal friction angle.

마찬가지로, 동일한 화산폭발지수와 층저마찰각을 설정하고 항복응력만을 다르게 한 것을 비교하였을 경우, 항복응력이 감소할수록 도달 범위가 증가하였음을 알 수 있다. 이것은 항복응력이 입자의 응집력으로 작용하여 화쇄류 입자의 움직임을 제한하고 중력으로 얻은 가속도에 대해 반대 방향, 즉 마찰력으로 작용하는 것으로 해석 가능하다.

동일한 화산폭발지수에서, 층저마찰각을 3°로 하였을 경우에 항복응력이 5,000 Pa, 10,000 Pa, 15,000 Pa로 변화할 때의 화쇄류의 피해 범위에 대한 결과를 시각적으로 비교하였다(그림 5).

Fig. 5.

Comparison of different yield stress. With the same VEI and basal friction angle (these are in case of 3°). Runout range of PDCs are increase in inverse proportion to yield stress.

또한 이것은 동일한 항복응력(그림 4)과 동일한 층저마찰각(그림 5)을 설정하였을 때, 화산폭발지수에 따라서 총 화산분출물의 양이 증가할수록 화쇄류의 도달 거리가 증가함을 의미한다. 화산폭발지수가 1 증가할수록 총 화산분출물의 양이 10배 증가하도록 설정하였으며, 따라서 형성되는 화쇄류의 양도 10배 증가하는 셈이 된다. 화쇄류가 도달하는 지역의 총 면적이 화산폭발지수가 증가함에 따라서 확연히 증가하는 것이 보여진다. 또한 화산폭발지수 3에서 화산폭발지수 5까지는 화쇄류가 주로 골짜기 부분에 퇴적되었으나, 화산폭발지수 6과 화산폭발지수 7에서는 영향 범위 내에서 골짜기와 능선을 가리지 않고 넓은 지역을 피복하는 것을 확인할 수 있다.

화산폭발지수 7의 시뮬레이션 결과를 밀레니엄 분화의 화쇄류 퇴적층이 발견되는 거리와 비교하여 보았다. 밀레니엄 분화의 화쇄류는 천지 칼데라로부터 성층화산체의 사면을 따라 평균 20~30 km, 북쪽계곡을 따라 최대 65 km, 서쪽 계곡을 따라 최대 40 km, 풍하 측에서는 최대 48 km까지 분포하며, 발생한 화쇄류의 부피는 1차 알칼리유문암질 화산활동에서 10 km³, 2차 조면암질 화산활동에서 7~10 km³ (총 17~20 km³)으로 추정하였다(Miyamoto et al., 2004). 본 연구의 수치모의결과 화산폭발지수 7의 경우 23.4 km까지 1 m의 층후가 나타나므로, 대략 20~30 km이내에서는 실제와 잘 일치하는 것으로 해석된다. 천 년 전에 비하여 현재 지형은 밀레니엄 화쇄류로 인하여 계곡 등이 매몰되는 변화가 있었으므로 계곡을 따라 더 멀리 진출하지는 않은 것으로 추정되며, 시뮬레이션 조건에서 화쇄류의 발생량을 10 km³ 으로 정하였으므로 부피 및 층저마찰값 등의 변수들을 조절하면 수치모의를 통한 밀레니엄 화쇄류의 보다 정확한 재현이 가능할 것이다. 일반적으로 TITAN2D 수치모의의 정확도는 지표 지질조사 결과와 비교하여 볼 때, 소규모 분화인 경우 54.4%, 대규모 분화인 경우 72.3%이며 VolcFlow의 경우에는 소규모 분화인 경우 68.3%, 대규모의 경우 53.8%의 정확도를 나타낸다고 보고되어 있다(Charbonnier et al., 2015).

5. 결 론

연구에서는 백두산에서 발생 가능한 화쇄류의 피해범위를 알아내어 대비하여 화쇄류로 인한 피해를 최소한으로 줄이기 위하여, 화쇄류의 도달 범위를 모의 가능한 여러 가지 수치 시뮬레이션 모델 중 VolcFlow 모델을 사용하고, 다양한 분화 모델을 상정하기 위하여 화산폭발지수 3, 4, 5, 6, 7에 대하여, 층저마찰각이 3°, 5°, 10°인 각각의 경우에, 역시 항복응력이 각각 5,000 Pa, 10,000 Pa, 15,000 Pa 인 경우를 가정하여, 총 45개 시나리오(표 2)에 대한 시뮬레이션을 실시하였다. 이를 통해 백두산에서 발생 가능한 화쇄류의 도달 범위를 모의하였다.

동일한 화산폭발지수, 즉 분출물의 총 부피가 동일한 경우에 층저마찰각을 3°, 5°, 10°로 달리 하였을 경우, 층저마찰각이 3° 일 때 화쇄류가 가장 멀리 도달하였다. 이것으로 층저마찰각이 작을수록 화쇄류가 더 멀리까지 도달함을 알 수 있었다. 마찬가지로 동일한 화산폭발지수에서 층저마찰각 역시 동일할 경우에 항복응력이 각각 5,000 Pa, 10,000 Pa, 15,000 Pa일 경우, 5,000 Pa일 때 화쇄류가 가장 멀리까지 도달하였으므로, 항복응력이 작을수록 화쇄류가 도달하는 거리가 증가함을 알 수 있었다. 이는 화쇄류에 의한 화산재해에서의 ‘최악의 경우’를 VolcFlow 프로그램을 통하여 모의할 경우, VolcFlow의 변수 설정 과정에서 층저마찰각 및 항복응력을 모의하고자하는 화쇄류의 특성이 가질 수 있는 가장 낮은 값으로 설정할 필요가 있다고 해석된다.

시뮬레이션 결과, 분화의 규모 즉 화산폭발지수가 증가함에 따라 화쇄류의 확산 범위는 점점 넓어지며, 분화구 중심으로부터 화쇄류의 최대 도달 거리는 층저마찰각 3°, 항복응력 5,000 Pa일 때, 화산폭발지수 3일 때 약 2.3 km, 화산폭발지수 4일 때 9.1 km, 화산폭발지수 5일 때 14.4 km, 화산폭발지수 6일 때 18.6 km, 화산폭발지수 7일 때 23.4 km까지 도달하였다.

상기의 결과를 백두산의 재해위험도 작성 시, 분화규모에 따른 화쇄류의 피해 범위 기준으로 설정 가능하고, 이를 통해 화산재해에 의한 피해를 최소화 할 수 있을 것이다.

Acknowledgments

본 논문을 읽고 건설적인 조언을 통해 문장을 개선해 주신 황상구, 손영관 교수, VolcFlow 수치모의 프로그램 적용에 많은 도움을 주신 Dr. Karim Kelfoun에게 감사드린다. 본 논문은 장철우의 2015년도 석사 학위논문의 내용을 발췌 정리하였다. 본 연구는 국민안전처 자연재해저감기술개발사업단(자연피해예측 및 저감연구개발사업)의 지원으로 수행한 ‘한반도 주변 화산분화 위험을 고려한 화산재해 대응체계 고도화’ [MPSS-자연-2015-81]과제의 성과입니다.

References

• Auker, M.R., Sparks, R.S.J., Siebert, L., Crosweller, H.S., and Ewert, J., (2013), A statistical analysis of the global historical volcanic fatalities record, Journal of Applied Volcanology, 2, p1-24. [https://doi.org/10.1186/2191-5040-2-2]
• Bonadonna, C., (2006), Probabilistic modelling of tephra dispersal, In: Mader, H., Cole, S., Connor, CB (eds), Statistics in Volcanology, IAVCEI Series Volume 1 Geological Society of London, p243-259.
• Bonadonna, C., Connor, C.B., Houghton, B.F., Connor, L., Byrne, M., Laing, A., and Hincks, T.K., (2005), Probabilistic modeling of tephra dispersal: Hazard assessment of a multiphase rhyolitic eruption at Tarawera, New Zealand, Journal of Goephysical Research, 110, p21. [https://doi.org/10.1029/2003JB002896]
• Branney, M.J., and Kokelaar, B.P., (2002), Pyroclastic density currents and the sedimentation of ignimbrites, Geological Society of London, Memoirs 27, p152.
• Charbonnier, C., Ogburn, S., Calder, E., and Gertisser, R., (2015), Field validation of pyroclastic density current (PDC) models: examples from Merapi and Soufriere Hills volcanoes, 26th IUGG General Assembly, VS06b: Benchmarking Pyroclastic Density Current Models: Code Inter-Comparison and Field Validation, Abstract IGUU-1142.
• Connor, L.J., and Connor, C.B., (2006), Inversion is the key to dispersion: Understanding eruption dynamics by inverting tephra fallout, In: Mader, H., Coles, S., Connor, C.B., and Connor, L.J. (eds), Statistics in Volcanology, IAVCEI Series Volume 1 Geological Society of London, p231-242.
• Constantinescu, R., Thouret, J.C., and Irimus, I.A., (2011), computer modeling as tool for volcanic hazards assessment: An example of pyroclastic flow modeling at El Misti volcano, southern Peru, Geographia Technica, 2, p1-14.
• Cui, D.X., Wang, Q.L., Li, K., Wang, W.P., and Hu, Y.X., (2007), Analysis of recent deformation of Changbaishan Tianchi volcano, Chinese Journal of Geophysics, 50, p1515-1524. [https://doi.org/10.1002/cjg2.1171]
• Davies, T., McSaveney, M., and Kelfoun, K., (2010), Runout of the Socompa volcanic debris avalanche, Chile; a mechanical explanation for low basal shear resistance, Bulletin of Volcanology, 72, p933-944. [https://doi.org/10.1007/s00445-010-0372-9]
• Gao, L., (2007), Recent geochemical variation of the hotspring gases from the Tianchi Volcano, Changbai Mountains, Northeast China, Earthquake Research in China, 21, p179-188.
• Guo, Z., Liu., J., Han, J., He, H., Dai, G., and You, H., (2006), Effect of gas emissions from Tianchi volcano (NE China) on environment and its potential volcanic hazards, Science in China, Series D, 49, p304-310. [https://doi.org/10.1007/s11430-006-0304-x]
• Harris, A.J.L., and Rowland, S.K., (2001), FLOWGO: A kinematic thermo-rheological model for lava flowing in a channel, Bulletin of Volcanology, 63, p20-44. [https://doi.org/10.1007/s004450000120]
• Horn, S., and Schmincke, H.U., (2000), Volatile emission during the eruption of Baitoushan Volcano (China/North Korea) ca. 969 AD, Bulletin of Volcanology, 61, p537-555. [https://doi.org/10.1007/s004450050004]
• Hurst, A.W., (1994), ASHFALL . A Computer Program for Estimating Volcanic Ash Fallout, Institute of Geological & Nuclear Science, New Zealand, Science Report, 94, p22.
• Kelfoun, K., and Druitt, T., (2005), Numerical modeling of the Socompa rock avalanche, Chile, Journal of Geophysical Research, 110, p13. [https://doi.org/10.1029/2005JB003758]
• Kelfoun, K., Duitt, T., van Wyk de Vries, B., and Guilbaud, M.N., (2008), Topography reflection of the Socompa debris avalanche, Chile, Bulletin of Volcanology, 70, p1169-1187. [https://doi.org/10.1007/s00445-008-0201-6]
• Kelfoun, K., Giachetti, T., and Labazuy, P., (2010), Landslide-generated tsunamis at Reunion Island, Journal of Geophysical Research, Earth Surface, 115, p17. [https://doi.org/10.1029/2009JF001381]
• Kelfoun, K., Samaniego, P., Palacios, P., and Barba, D., (2009), Testing the suitability of frictional behaviour for pyroclastic flow simulation by comparison with a well-constrained eruption at Tungurahua volcano (Ecuador), Bulletin of Volcanology, 71, p1057-1075. [https://doi.org/10.1007/s00445-009-0286-6]
• Laboratoire Magmas et Volcans, (2015), http://lmv.univ-bpclermont.fr/volcflow (May 2, 2015).
• Liu, G., Yang, J.K., Wang, L.J., and Sun, J.C., (2011), Analysis of Tianchi volcano activity in Changbai Mountain, NE China, Global Geology, 14, p44-53.
• Macedonio, G., Costa, A., and Longo, A., (2005), A computer model for volcanic ash fallout and assessment of subsequent hazard, Computers & Geosciences, 31, p837-845. [https://doi.org/10.1016/j.cageo.2005.01.013]
• Machida, H., and Arai, F., (1983), Extensive ash falls in and around the Sea of Japan from large late Quaternary eruptions, Journal of Volcanology and Geothermal Research, 18, p151-164. [https://doi.org/10.1016/0377-0273(83)90007-0]
• Machida, H., Arai, F., and Moriwaki, H., (1981), Two Korean tephras, Holocene markers in the Sea of Japan and the Japanese Islands, Kagaku, 51, p562-569, (in Japanese).
• Machida, H., Moriwaki, H., and Zhao, D.C., (1990), The recent major eruption of Changbai Volcano and its environmental effects, Geographical Reports of Tokyo Metropolitan University, 25, p1-20.
• Mastin, L.G., (2001), A simple calculator of ballistic trajectories for blocks ejected during volcanic eruptions, USGS Open-File Report 01-45, p16, (version 1.2 online November 2009).
• Miyamoto, T., Kanno, H., Okuno, M., Nasu, H., and Makohonienko, M., (2010), Reconstruction of volcanic activities occurring in Baitoushan volcano after 10th century huge eruption, In: Taniguchi, H. (eds), Earth Science of Baitoushan Volcano and its Adjacent Area, Center of Northeast Asian Studies (CNEAS) Tohoku University, Monograph Series 41 p123-141, (in Japanese with English abstract).
• Miyamoto, T., Nakagawa, M., Tanaka, Y., and Yoshida, M., (2004), Eruptive sequence of the 10th century Baitoushan eruption, CNEAS Monograph Series No.16, The Center for Northeast Asian Studies, Tohoku University, 218, p15-43, (in Japanese with English abstract).
• Muñoz, S.E., Castillo, R.M., Manea, V., and Palacios, D., (2009), Lahar flow simulations using LAHARZ program : Application for the Popocatepetl volcano, Mexico, Journal of Volcanology and Geothermal Research, 182, p13-22. [https://doi.org/10.1016/j.jvolgeores.2009.01.030]
• Newhall, C.G., and Self, S., (1982), The Volcanic Explosivity Index (VEI): an estimate of explosive magnitude for historical volcanism, Journal of Geophysical Research, 87, p1231-1238. [https://doi.org/10.1029/JC087iC02p01231]
• Procter, J.N., Cronin, S.J., Platz, T., Patra, A., Dalbey, K., Sheridan, M.F., and Neall, V., (2010), Mapping block-and-ash flow hazard based on Titan 2D simulations: a case study from Mt. Taranaki, NZ, Natural Hazards, 53, p483-501. [https://doi.org/10.1007/s11069-009-9440-x]
• Rowley, P.J., (2010), Analogue modelling of pyroclastic density current deposition, Ph.D. Thesis, London, UK, p298.
• Schilling, S.P., (1998), LAHARZ: GIS Program for Automated Mapping of Lahar Inundation Hazard Zones: U.S, Geological Survey Open-File Report 98-638, p80.
• Shangguan, Z.G., and Sun, M.L., (1997), 1997, Mantle-derived raregas releasing features at the Tianchi volcanic area, Changbaishan Mountains, Chinese Science Bulletin, 42, p768-771. [https://doi.org/10.1007/BF03186974]
• Sheridan, M.F., Hubbard, B., Carrasco-Nunez, G., and Siebe, C., (2000), GIS model for volcanic hazard assessment: pyroclastic flows at Volcan Citlaltepetl, Mexico, 4th International Conference on Integrating GIS and Environmental Modeling (GIS/EM4): Problems, Prospects and Research Needs, Banff, Alberta, 69, p209-221.
• Sheridan, M.F., Stinton, A.J., Patra, A., Pitman, E.B., Bauer, A., and Nichita, C.C., (2005), Evaluating Titan2D mass-flow model using the 1963 Little Tahoma Peak avalanches, Mount Rainier, Washington, Journal of Volcanology and Geothermal Research, 139, p89-102. [https://doi.org/10.1016/j.jvolgeores.2004.06.011]
• Simkin, T., and Siebert, L., (1994), Volcanoes of the world, Geoscience Press, Washington DC, USA, p379.
• Soh, W.J., and Yun, S.H., (1999), A review of the Holocene major eruption of Mt. Paektu volcano, Journal of Korean Earth Science Society, 20, p534-543, (in Korean with English abstract).
• Sulpizio, R., Capra, L., Sarocchi, D., Saucedo, R., Gavilanes-Ruiz, J.C., and Varley, N.R., (2010), Predicting the block-and-ash flow inundation areas at Volcan de Colima (Colima, Mexico) based on the present day (February 2010) status, Journal of Volcanology and Geothermal Research, 193, p43-66. [https://doi.org/10.1016/j.jvolgeores.2010.03.007]
• Vargas, R.F., Thouret, J.,C., van Westen, C., Sheridan, M.F., Siebe, C., Marino, J., Souriot, T., and Stinton, A., (2010), Mapping and assessing volcanic and flood hazards and risks with emphasis on lahars, in Arequipa, Peru, Geological Society of America Special Paper, 464, p265-280.
• Wei, H., Taniguchi, H., and Liu, R., (2002), Chinese myths and legends for Tianchi volcano eruptions, Northeast Asian Studies, 6, p191-200.
• Wei, H.Q., Liu, G.M., and Gill, J., (2013), Review of eruptive activity at Tianchi volcano, Changbaishan, northeast China: implications for possible future eruptions, Bulletin of Volcanology, 75, p1-14. [https://doi.org/10.1007/s00445-013-0706-5]
• Wei, H.Q., Wang, Y., Jin, J., Gao, L., Yun, S.H., and Jin, B., (2007), Timescale and evolution of the intracontinental Tianchi volcanic shield and ignimbrite-forming eruption, Changbaishan, Northeast China, Lithos, 96, p315-324. [https://doi.org/10.1016/j.lithos.2006.10.004]
• Wu, J.P., Ming, Y.H., Zhang, H.R., Liu, G.M., Fang, L.H., Su, W., and Wang, W.L., (2007), Earthquake swarm activity in Changbaishan Tianchi volcano, Chinese Journal of Geophysics, 50, p938-946. [https://doi.org/10.1002/cjg2.1111]
• Xu, J., Liu, G., Wu, J., Ming, Y., Wang, Q., Cui, D., Shangguan, Z., Pan, B., Lin, X., and Liu, J., (2012), Recent unrest of Changbaishan volcano, northeast China: a precursor of a future eruption?, Geophysical Research Letters, 39, p7. [https://doi.org/10.1029/2012GL052600]
• Xu, J.D., Pan, B., Liu, T.Z., Hajdas, I., Zhao, B., Yu, H.M., Liu, R.X., and Zhao, P., (2013), Climatic impact of the Millennium eruption of Changbaishan volcano in China: New insights from high-precision radiocarbon wigglematch dating, Geophysical Research Letters, 40, p54-59. [https://doi.org/10.1029/2012GL054246]
• Yun, S.H., (2013), Volcanological interpretation of historic eruptions of Mt. Baekdusan volcano, Journal of Korean Earth Science Society, 34, p456-469, (in Korean with English abstract). [https://doi.org/10.5467/JKESS.2013.34.6.456]
• Yun, S.H., Chang, C.W., and Kim, S.K., (2014), Distribution of pyroclastic density currents determined by numerical model at Mt. Baekdu volcano, Journal of Petrological Society of Korea, 23, p351-366, (in Korean with English abstract). [https://doi.org/10.7854/JPSK.2014.23.4.351]
• Yun, S.H., and Cui, Z.X., (1996), Historical eruption records on the Cheonji caldera volcano in the Mt. Paektu, Journal of Korean Earth Science Society, 17, p376-382, (in Korean with English abstract).
• Yun, S.H., and Koh, J.S., (2014), Petrochemical characteristics of volcanic rocks of historic era at Mt. Baekdusan, Journal of the Geological Society of Korea, 50, p753-769, (in Korean with English abstract). [https://doi.org/10.14770/jgsk.2014.50.6.753]
• Yun, S.H., and Lee, J.H., (2011), Volcanological interpretation of historic record of 1702 fallout-ash from the Mt. Baegdusan, Journal of Petrological Society of Korea, 20, p243-250, (in Korean with English abstract). [https://doi.org/10.7854/JPSK.2011.20.4.243]
• Yun, S.H., and Lee, J.H., (2012), Analysis of unrest signs of activity at the Baegdusan volcano, Journal of Petrological Society of Korea, 21, p1-12, (in Korean with English abstract). [https://doi.org/10.7854/JPSK.2012.21.1.001]
• Yun, S.H., Lee, J.H., Kim, S.K., Chang, C.W., Cho, E., Yang, I.S., Kim, Y.J., Kim, S.H., Lee, K.H., Kim, S.W., and Macedonio, G., (2013), TITAN2D simulations of pyroclastic flows from small scale eruption at Mt. Baekdusan, Journal of Korean Earth Science Society, 34, p615-625, (in Korean with English abstract). [https://doi.org/10.5467/JKESS.2013.34.7.615]
• Yun, S.H., Taniguchi, H., Wei, H., and Liu, J., (2007), Volcanic crisis of the Baegdusan, Abstract of 2007 Joint Conference of the Geological Science & Technology of Korea, p130-132, (in Korean).
• Yun, S.H., Won, C.K., and Lee, M.W., (1993), Cenozoic volcanic activity and petrochemistry of volcanic rocks in the Mt. Paektu area, Journal of Geological Society of Korea, 29, p291-307, (in Korean with English abstract).