
Network science approaches for analyzing regional interactions of sea surface temperature
Copyright ⓒ The Geological Society of Korea 2024
Abstract
Understanding the complex “warming chain” in sea regions is crucial for predicting the cascading impacts of oceanic heat interactions on global climate stability. This study employs network analysis to explore the interactions of sea surface temperature (SST) across oceanic regions, focusing on complex heat transfer dynamics. By applying a heat equation approach, sea regions are represented as nodes and their directional heat transfer relationships as edges, allowing the identification of key oceanic regions in terms of inward and outward heat distributions. The analysis highlights previously reported influential oceanic communities, such as those linked to the El Niño-Southern Oscillation (ENSO) system and the mutual interactions between the Indian and Atlantic Oceans, and underscores the role of these regions in global heat distribution, offering insights into oceanic temperature dynamics and potential implications for climate stability.
초록
해양 지역 간 복잡한 “온난화 연쇄 작용”을 이해하는 것은 해양 열 상호작용이 지구 기후 안정성에 미치는 연쇄적인 영향을 이해하고 예측하는 데 매우 중요하다. 본 연구는 네트워크 분석을 활용하여 해수면 온도(SST)의 지역 간 상호작용과 복잡한 열 전달 동역학을 분석하였다. 열 방정식 접근법을 적용하여 해양 지역을 노드로, 방향성을 가진 열 전달 관계를 엣지(link)로 표현함으로써, 열의 유입과 유출 분포 측면에서 중요한 해양 지역을 네트워크 과학의 중심성 측정법을 활용하여 식별하였다. 얻어진 결과는 엘니뇨-남방진동(ENSO) 시스템과 인도양 및 대서양 간 상호작용과 같이 이미 보고된 영향력 있는 해양 커뮤니티들의 상호작용을 강조하며, 이러한 지역들이 전 지구적 열 분포에서 가지는 기능적 역할을 이해하는데에 도움을 준다. 이 연구는 해양 온도 역학으로 얻어진 상호작용이 기후 안정성에 미칠 잠재적 함의에 대한 통찰을 제공할 수 있다.
Keywords:
network analysis, community, sea surface temperature, ocean interactions, climate dynamics키워드:
네트워크 분석, 커뮤니티, 해수 표면 온도, 해수 상호작용, 기후 동역학1. Introduction
The complex interactions between various sea regions play a crucial role in shaping the global climate system. In particular, understanding the interactions between sea surface temperatures (SST) of different oceanic regions is essential, as it regulates the Earth's climate system and significantly impacts weather patterns, ocean circulation, and marine ecosystems (Deser et al., 2010; Boers et al., 2019; Robertson et al., 2000; Lapointe et al., 2020; Peng et al., 2024).
Recent studies, for example, have emphasized the critical influence of the Indian Ocean on climate anomalies and sea temperature changes (Hu and Fedorov, 2020; Yang et al., 2022). Among them, one study has observed climate anomalies in the North Atlantic Ocean in relation to the Indian Ocean, specifically focusing on the phenomenon known as the North Atlantic Warming Hole (NAWH) (Hu and Fedorov, 2020). The NAWH refers to a region in the North Atlantic that experiences a cooling trend in contrast to the overall warming observed elsewhere, which has significant implications for both regional and global climate patterns. The cause of the NAWH is still debated and has been linked to several factors, including changes in ocean currents (Clement et al., 2018), and atmospheric circulation patterns (Josey et al., 2019; Lozier et al., 2019; Hu and Fedorov, 2020). In particular, it is known that warming in the Indian Ocean, driven by increased greenhouse gas emissions, affects the North Atlantic through complex atmospheric and oceanic teleconnections. This warming connection is an example of a “warming chain” between distant oceanic regions and provides an important context for understanding changes in the global climate system.
Another study also identified an interactive warming chain between the Indian Ocean and the Atlantic Ocean (Yang et al., 2022). The authors found that the interaction between the Indian Ocean and the North Atlantic Ocean amplifies the warming trend in both regions through atmospheric teleconnections. Additionally, the researchers observed that the Pacific Ocean plays a modulatory role in this warming chain. This is another example of how interconnected warming across different oceanic regions contributes to regional temperature increases.
El Niño-Southern Oscillation (ENSO) also plays a crucial role in modulating SST across the tropical Pacific and has far-reaching effects on global climate systems. As discussed by McPhaden et al. (McPhaden et al., 2006), ENSO acts as an integrating concept in Earth science by linking atmospheric and oceanic processes, which together drive significant variations in SST. During El Niño events, warmer-than-average SSTs spread across the central and eastern tropical Pacific, altering atmospheric circulation patterns and affecting global climate phenomena such as rainfall distribution, storm formation, and even temperature anomalies in remote regions. This may be another element in the warming chain of SST. However, the comprehensive interactions among these various sea regions remain poorly understood, as conventional methods often analyze SST by focusing on specific regions.
In this study, we employ network analysis to investigate the regional interactions involving SST across various oceanic regions, addressing the gap in research on the comprehensive “warming chain” between different sea regions. By applying a heat equation approach, we represent sea regions as nodes and the heat transfer relationships between them as edges, allowing us to examine the overall network of heat interactions. This approach enables us to identify possible key regions that can drive SST variability and uncover the underlying structures that govern these complex interactions. By visualizing and quantifying the structural characteristics of the interactions, we gain a comprehensive understanding of the heat distributions across the entire oceanic system, emphasizing the broader context of heat transfer and inter-regional influences that are often overlooked in conventional analyses.
2. Data and Methods
In this study, we apply the heat equation from statistical physics to explore directional interactions in the SST dataset.
2.1. Sea Surface Temperature Dataset and Preprocessing
We utilize the optimum interpolation Sea Surface Temperature (SST) dataset version 5 from National Oceanic and Atmospheric Administration (NOAA, USA) (NOAA). This dataset is a high-resolution (2° × 2°) global analysis of SST, produced by blending satellite observations, ship, and buoy data. The SST dataset provides daily SST values, which are optimally interpolated to fill data gaps, and this preprocess makes the dataset suitable for climate monitoring and long-term trend analysis. Version 5 of the dataset includes updated algorithms for better bias correction and improved accuracy in regions with sparse in-situ observations. This dataset is widely used in oceanographic and climate studies due to its consistency and high temporal resolution, making it an ideal choice for analyzing regional SST interactions. In this study, data from 1979 to 2019 were utilized for the analysis, and to analyze the temperature dataset, we calculated the average temperature for each cell over the target period, then subtracted this average from all temperature data points within that cell.
2.2. Heat Equation Approach
In statistical physics, the temporal evolution of a spatially distributed temperature field is often described by the heat equation, where denotes the position vector, and t represents time. The mathematical form of the heat equation is as follows:
| (1) |
Here, ∇2 is the Laplacian, the second-order spatial derivatives of temperature, and D represents thermal diffusivity, indicating the sensitivity of a point to temperature differences in its vicinity. The Laplacian yields negative values when the temperature is higher than the average temperature of the surroundings and positive values when the temperature is lower.
In discrete spaces, Eq (1) can be rewritten as
| (2) |
where index i denotes spatial positions, and τ is time interval of the observed temperature. The M matrix represents the diffusivity of each cell, and the elements of the Laplacian matrix L, calculated as K − A, where K is a diagonal matrix containing the number of neighboring locations for each cell, and A is the adjacency matrix, thus analogously representing the Laplacian operator in continuous space.
The heat equation is typically considered in uniform spaces where interactions among neighboring nodes are equal, similar to an unweighted network. However, in the real world, non-uniform interactions between regions are expected in phenomena such as ocean currents and atmospheric teleconnections. This leads us to consider a weighted and directed network scenario, where the off-diagonal elements of MiLij can take any real value. Here, the real-valued elements represent the weighting of how much a position of a node j influences node i, based on temperature. The previously discussed MiLij is extended to a generalized Laplacian matrix, Wij, which represents the relative influence of j on i. These weights need not be symmetric. In this case, the diagonal elements Wii become −. For example, in a network with uniform temperature Ti = Tj =T, there would be no temporal variation in temperature at any node, leading to .
To determine Wij which best explains the given spatio-temporal SST data T under the aforementioned conditions, the equation suggests that a suitable Wij should satisfy the following criteria:
| (3) |
and Eq. 3 can be applied to an objective function of . By applying the Adam optimization to minimize the error, one can begin with the Laplacian matrix of the fully connected network as the initial Wij. Since the update rule for Wij must also account for changes in Wii due to constraints that preserve the sum of Wij in Wii, the equation can be rewritten as follows:
| (4) |
where . With a learning rate β, one can update Wij as
| (5) |
Here, s denotes the updating step, and δs represents the interval between the updating time steps. Please note that, during the simulation, any change that would result in a positive Wij will be used. It means off-diagonal components of Wij were kept positive by setting any negative values to zero.
2.3. Construction of Backbone Network
To extract the backbone of the SST network, we applied the method proposed by Serrano et al. (Serrano et al., 2009). This technique identifies the most significant connections in a weighted network by statistically filtering out less relevant links. Specifically, for each node, the algorithm evaluates the weights of its edges and compares them to a null model of random edge assignments. This method allows us to retain only those edges that exhibit statistically significant interactions, effectively reducing the complexity of the network while preserving its essential structure. In our analysis, we set the significance level to β = 0.1, meaning that only links satisfying the significance level were retained.
Starting from the weighted matrix W, derived from applying the heat equation approach to the SST data, we extracted the SST backbone network. This filtered network highlights the significant interactions between sea regions, offering a clearer understanding of the underlying patterns in SST variations. After having the backbone network with β = 0.1, the total number of nodes in original backbone network is 9,958, and with 1,555,158 directed edges.
2.4. Louvain Community Detection
The Louvain community detection algorithm is a widely used method for identifying communities in large networks by optimizing modularity. Modularity is a measure that compares the density of edges within communities to the density of edges between communities (Blondel et al., 2008; Dugué et al., 2015). The modularity Q for a directed weighted network is mathematically expressed as:
| (6) |
where Aij is the adjacency matrix of the network, in and out are the incoming degrees of nodes i and outgoing degrees of node j, m is the total number of edges. In this equation, ci and cj represent the communities to which nodes i and j belong, and δ(ci, cj) is 1 if nodes i and j are in the same community and 0 otherwise. The Louvain algorithm works in two phases. In the first phase, each node is assigned to its own community, and nodes are iteratively moved to neighboring communities to locally maximize the modularity. In the second phase, nodes belonging to the same community are aggregated into a single super-node, and the algorithm is reapplied to this reduced network. The process continues until no further improvements in modularity can be made, allowing the detection of hierarchical community structures at multiple scales. In the current study, we employed the Louvain algorithm from Python’s NetworkX package, using the default resolution parameter of 1, and a convergence threshold of 10-7.
2.5. Building the Community Network
Each detected community with the Louvain algorithm represents a group of nodes, that have stronger interactions with one another compared to nodes outside the community. In this study, a group of nodes in the backbone network represents the positions of sea surface areas divided into a grid.
To simplify the interaction structures between sea regions, we constructed a new network from the backbone with community indexes, where each node in this new network represents an entire community identified in the backbone network. The connectivity between these new community nodes was established by aggregating the original links between nodes in the backbone that belonged to each pair of communities. In this aggregation, we only considered strong link weights greater than 10-3. This process resulted in a community-level network with 12 nodes, where the edges represent the total weight of the connections between communities. This community-level network provides insights into the interactions among different sea region communities, enabling us to observe higher-order patterns and relationships between key regions within the backbone structure.
2.6. Network Centralities
Betweenness centrality measures the importance of a node based on the number of shortest paths passing through it. If a node lies on many shortest paths between other pairs of nodes, it has a high betweenness centrality, indicating that it acts as a bridge in the network. Mathematically, betweenness centrality for a node v is defined as:
| (7) |
where σst is the total number of shortest paths from node s to node t, and σst(v) is the number of those paths that pass through node v(Freeman, 1977; Newman, 2018).
Eigenvector centrality assesses the importance of a node based on the importance of its neighbors. A node connected to many highly influential nodes has a high eigenvector centrality. It is defined as the eigenvalue equation:
| (8) |
where CE (v) is the eigenvector centrality of node v, Avu is the adjacency matrix element between nodes v and u, and λ is the largest eigenvalue of the adjacency matrix (Bonacich, 1972; Newman, 2018).
In directed networks, the centrality of nodes can be evaluated using left and right eigenvector centrality. These measures are derived from the eigenvectors of the network's adjacency matrix A and help capture different aspects of influence within the network. For a given adjacency matrix A, right eigenvector centrality () is obtained from the eigenvalue equation . Here, represents the importance of nodes based on the inbound connections from other influential nodes, with λ being the eigenvalue. Right eigenvector centrality measures how much a node benefits from being connected to other important nodes, emphasizing the inbound influence of each node. This is particularly useful for assessing the significance of nodes that receive links from many highly connected nodes.
On the other hand, left eigenvector centrality () is computed by considering the transpose of the adjacency matrix, satisfying the equation . In this context, represents the influence that each node has on others, providing insights into the outbound influence of the nodes. This approach helps in understanding how much a node contributes to the importance of the nodes it points to, effectively quantifying its role in spreading influence. In our analysis, we utilize both right and left eigenvector centrality to evaluate the dual nature of influence in the backbone network of optimized weights derived from heat equation approach—how nodes receive influence and how they exert influence on others, providing a comprehensive picture of their roles in the network dynamics of heat transfer.
Edge Betweenness Centrality is a measure used to identify the importance of edges in a network by evaluating their role in shortest paths between node pairs [Brandes, 2008]. Specifically, the edge betweenness centrality of an edge e is defined as the sum of the fraction of all-pairs shortest paths that pass through edge e. If σst represents the number of shortest paths between nodes s and t, and σst represents the number of those paths that pass through edge e, the edge betweenness centrality B(e) is given by:
| (9) |
This measure is particularly useful for understanding which connections (edges) in the network are critical for maintaining communication between various nodes.
High edge betweenness indicates that an edge acts as a bridge that connects different parts of the network, suggesting its crucial role in maintaining network cohesion. In our analysis, we calculated edge betweenness centrality for each edge to determine the most influential connections in the community network. Edges with high edge betweenness are often critical for the flow of information or other types of interactions within the network, as they participate in a significant portion of the shortest paths. This is particularly relevant in understanding the role of certain routes in spreading influence across the network and in identifying potential bottlenecks that could disrupt connectivity if removed. By identifying edges with high betweenness, we can gain insights into the overall resilience and structure of the network.
3. Results
3.1. Regions with strong inward and outward weights from heat equation approach
Fig. 1 demonstrates significant spatial variation in the adjusted inward and outward flow weights derived from the heat equation approach. Regions A (the North Pacific) and B (the Indian Ocean) in panel (a) are characterized by high inward flow, suggesting a possible strong heat concentration of influences within these areas. Conversely, regions A, C (ENSO), D (NAWH), and E (the Southern Atlantic Ocean) in panel (b) exhibit high outward flow, indicating that these areas might act as major sources of heat transfer, distributing their heat flow across the network. The black arrows in both panels illustrate the sum of directional flows for each point, providing insights into the overall movement dynamics. Specifically, the directional vector at each location i, denoted as , is determined by its relationship with surrounding nodes positioned in the eight directions around i—namely, below, left, right, and the four diagonal directions. For each pair (i,j), the location vectors for i, and j are represented as , and , respectively. From the location vectors, the unit vector representing the direction from i to j is denoted as . By using Wij as the weight associated with the direction from j to i, we can define the weighted sum at location i as follows:
| (10) |
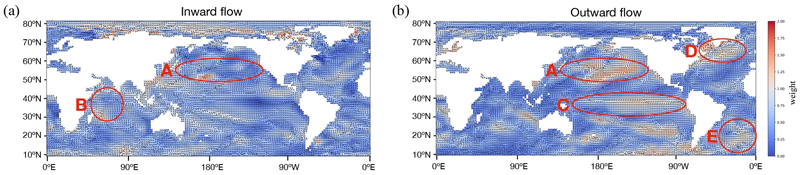
Adjusted inward and outward weights derived from the heat equation approach. The weights Wij from the heat equation method have been adjusted to range from 0 (blue) to 2 (red). Panel (a) illustrates the adjusted inward weights, while panel (b) shows the adjusted outward weights. The black arrows represent the sum of flow directions at each point’s surrounding positions. High inward flow regions are indicated as regions A and B in panel (a), while high outward flow regions are labeled as regions A, C, D, and E in panel (b).
These directional relationships highlight key regions that play crucial roles in the inward and outward heat transfer, which may have implications for understanding underlying processes such as oceanic circulation or climate phenomena.
For example, regions B, D, and E, located in the Indian Ocean, the North, and South Atlantic Ocean, respectively, are known for their interrelated heat transfer interactions (Hu and Fedorov, 2020; Yang et al., 2022). These regions are highlighted in Fig. 1a and Fig. 1b, showing strong inward flow for region B and a strong outward flow for region E. Additionally, the North Atlantic Warming Hole (NAWH) is marked as region D in Fig. 1b, showing strong outward flows. Given that the causes of the NAWH are still under debate, this result offers a new perspective on the oceanic heat transfer interactions related to this phenomenon and its connection to other sea regions.
Moreover, the primary region of El Niño-Southern Oscillation (ENSO) in the Pacific Ocean is highlighted as region C, indicating a strong outward flow in Fig. 1b. This result demonstrates that the weights derived from the heat equation can capture directional heat transfer relationships, which have been limited in conventional analyses.
3.2. Structural and Spatial Characteristics of Backbone Network
Since the heat equation approach provides directional weights of heat transfer flows, one can analyze directional relationships by transforming them into a heat transfer weight network. While the structural analysis of directional and weighted network can reveal crucial insights into the connectivity patterns and spatial relationships within the oceanic heat transfer network, its dense connectivity can obscure the identification of primary structures. Therefore, extracting the backbone network is essential to focus on the most significant connections and better understand the key components of the system. To this end, we applied a backboning algorithm (see Methods, (Serrano et al., 2009)) to extract statistically significant weighted links.
The in-degree and out-degree distributions of the original network show a characteristic pattern that can be well-described by a log-normal distribution (Fig. 2a). This type of distribution may indicate highly heterogeneous connectivity, with a few nodes having substantially more links than others, depending on the mean and standard deviation. To assess the heterogeneity of in-degree and out-degree distributions, we performed power-law fitting on their tails (Fig. 2b). As observed, the in-degree distribution exhibits an exponent close to 2, demonstrating a heavy-tail tendency. In contrast, the out-degree tail shows an exponent close to 9, which is relatively large and less characteristic of a heavy-tail property. A distribution like in-degree distribution is typical in natural systems, where certain regions play a dominant role in either collecting or distributing influence, further emphasizing the complex dynamics of heat transfer within the ocean.
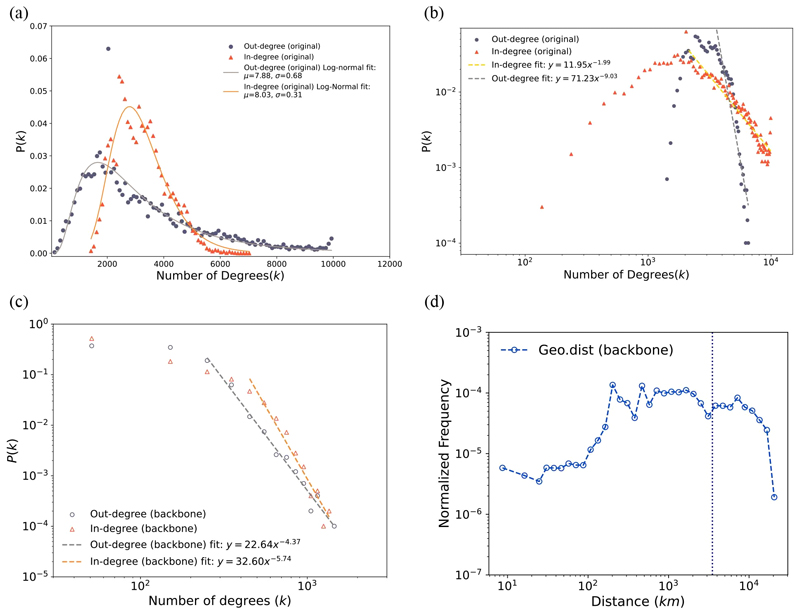
Structural characteristics of the backbone network derived from directional weights. (a) The in-degree and out-degree distributions of the original network derived from the directional and weighted interactions shown in Fig. 1. Circle markers indicate the empirically observed frequency of the number of outgoing links, while triangle markers represent the number of incoming links. The grey and red solid lines show the log-normal fits for the outgoing and incoming links, respectively. (b) Degree distributions of the original correlation networks (on log-log axes), with tail-part fitting applied to the distributions. (c)The distribution of the number of in-degree and out-degree for the backbone network (α = 0.1, see Methods), with markers indicating the relative frequency of each type of degrees, are shown. The fitted tail distributions are shown with dashed lines in red (for in-degree) and grey (for out-degree). (d) Geodesic distance distribution between nodes, calculated based on the center of each cell within the backbone network, highlighting the spatial relationships between nodes. The distances range from 10 km to 20,000 km. The vertical dotted line indicates the starting point of the second peak in long-range distances between nodes (≥3,500 km).
On the other hand, the in-degree and out-degree distributions of the backbone network exhibit power-law behavior, with exponent of 5.74 and 4.37, respectively, as shown in Fig. 2c. Due to the large exponent values, it is challenging to conclude that the distribution exhibits a heavy-tail property. However, this distribution still demonstrates that, after extracting statistically significant links, a few nodes retain a large number of connections (more than links), while most nodes have fewer than 200 links.
In terms of spatial characteristics of the backbone network, Fig. 2d shows the geodesic distance distribution between nodes, revealing that connections between nodes span a wide range of distances, from localized interactions (10 km) to broader, ocean-basin scale connections (up to 20,000 km). This diversity in connection lengths suggests a multiscale structure of heat transfer in sea regions, where both local and global interactions are essential for maintaining the heat transfer backbone network's overall connectivity.
3.3. Communities in Backbone Network
To identify key regions and their connectivity patterns in the backbone network, we performed community detection using the Louvain algorithm (see Methods). In particular, we used links spanning more than 3,500 km to focus on the long-range interactions between sea regions, as 3,500 km represents a starting point (a mid point between 3,000 km and 4,000 km) of the second peak in the distribution of long-range interactions (Fig. 2d). The community detection results in Fig. 3a reveal a clear structural organization within the backbone network, highlighting the distinct communities formed as a result of long-range directional heat transfer interactions.This structure is maintained when the distance criterion is 3,000 km. Panel (a) shows the complete set of communities within the backbone network, with the previously marked regions (A, B, C, D, and E) overlaid on the community structure. The detected communities, each represented by a different color, exhibit unique spatial patterns, indicating the presence of highly interconnected regions across multiple scales of distance. This differentiation allows us to better understand how various parts of the ocean interact and identify the dominant areas of influence in oceanic heat transfer.
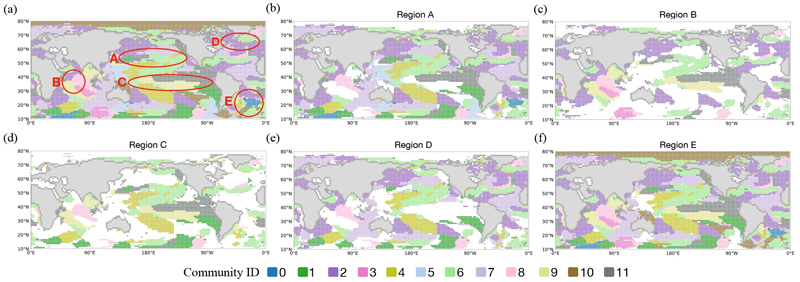
Community detection in the long-range backbone network and regional categorization. (a) Community structure of the entire long-range backbone network derived from the directional weights, with marks of previous regions labeled as A, B, C, D, and E. The detected communities are represented by different colors based on their community ID (from 0 to 11). (b-f) panels show detailed community distribution for each marked region: (b) Region A, (c) Region B, (d) Region C, (e) Region D, and (f) Region E. Each panel highlights the communities within the corresponding region, revealing the spatial distribution and boundaries of the identified communities.
In the detailed views provided in panels (b) to (f), each region is analyzed individually to highlight its community structure. Region A, as shown in panel (b), contains nine communities, including most of the communities except for those in parts of the Indian and Pacific area (community 9) and the North Pole (community 10), each with distinct spatial boundaries. On the other hand, regions B and C, as shown in Fig. 3c and 3d, include a relatively smaller number of communities compared to region A. Notably, region B, which is primarily located in the Indian Ocean, includes communities 6, 9, and 11, which are part of the ENSO system. Additionally, this region contains community 2, and 6, which is largely related to the North Atlantic Ocean. Region C also highlights the ENSO system, including its relationships with the Indian and Atlantic Oceans.
Region D, which mostly represents the NAWH, is characterized by more diffuse community boundaries involving communities 2, 6, and 7, possibly indicating a broader influence from all sea areas, including the near the South Pole area, and the Indian Ocean. In contrast, region E resembles region A, as it contains a large portion of the communities, including the North Pole area, suggesting that the Southern Atlantic Ocean has a highly mixed influence from other sea communities. Overall, the spatial categorization of these communities reveals the multiscale nature of heat transfer in the ocean, highlighting previously reported crucial connections among the Indian, Atlantic, and Pacific Oceans.
3.4. Centralities of Communities with Total Weights and Averaged Weights
To understand the directional and weighted flow between communities, we reconstructed the community network by aggregating the directional weighted links between them (see Methods). In this network, each community is represented as a node, and all connections within a community have been merged into a single directed weighted link to another community. When merging these links, we used both the average weights and the total weights as they represent different aspects of the relationships between communities (see Methods). On this networkwe applied centrality measures to both nodes and edges, using network science techniques to identify the functional role of each community in sea surface heat transfer.
Fig. 4 highlights the identification of key communities within the network of oceanic communities using betweenness centrality as a measure of importance (see Methods). Specifically, in panel (a), betweenness centrality was calculated using average weights, which is normalized by the number of links, allowing us to determine which communities play a central bridging role per unit link between different parts of the network. As shown in Fig. 4b, community 8, 11, and 9 play crucial roles as bridges connecting various other communities, with their representative region being the ENSO system. This result indicates the possibility that a significant portion of the ENSO system may act as channels for heat transfer between other communities.
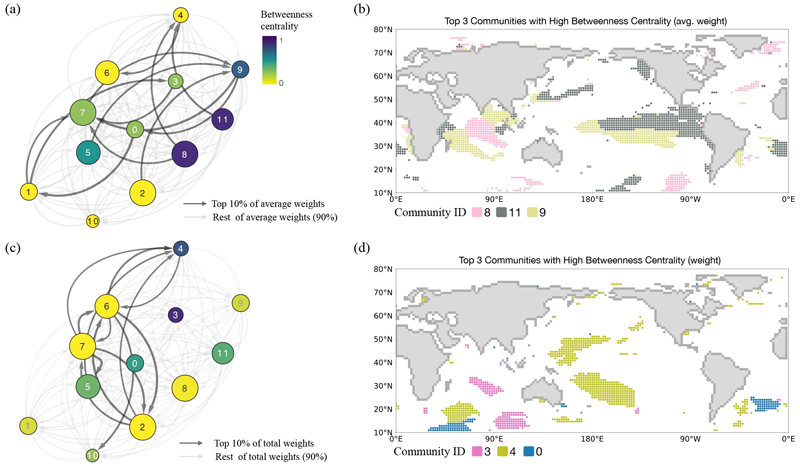
Identification of key communities using betweenness centrality in the network of sea region communities. (a) A network between communities shows betweenness centrality measured for the communities (nodes), using average weights normalized by the number of links between them. Node colors represent the strength of each node (each community)'s betweenness centrality, with the top 10% of average weights (13 edges) highlighted in darker grey. (b) The top 3 communities with the highest betweenness centrality from (a) are shown. (c) Betweenness centrality on the same network as in (a) is calculated using total weights instead of average weights, with nodes colored according to their betweenness centrality. The top 10% of edges by total weight (13 edges) are also highlighted in darker grey. (d) The map highlights the top 3 regions with the highest betweenness centrality based on (c). The node size is determined based on the number of links, both incoming and outgoing.
In panel (c), betweenness centrality was recalculated using total weights rather than average weights, providing insight into the overall influence of each oceanic community by considering the strength of all connections. Fig. 4d maps the top three regions (communities 3, 4, and 11) with the highest betweenness centrality, which are primarily located in the South Polar areas and the periphery parts of ENSO system. This result emphasizes their crucial function in global oceanic connectivity, particularly when considering their overall influence. These findings highlight the specific roles of oceanic communities, namely the ENSO system and polar regions, in heat distribution throughout the ocean. Considering the structure of community networks in Figs. 4a, and 4c, the ENSO system-related communities (4, 9, and 11) have relatively weak but diverse inward connections from most other communities in both cases, with particularly strong connections between community 4 and communities 2, 5, 6, and 7 (closely related to the South Pole, Indian Ocean, and parts of the Pacific Ocean) in terms of total weights. Regarding the average weights, the ENSO-related communities receive inward flows from communities 2, 5, 6, and 8 (which are more diffuse), and direct outflows to other communities (0, 6, and 7), which are located near the periphery of the ENSO system, as well as the Indian and Atlantic Oceans. This provides insight into the role of the ENSO system, suggesting that its crucial impact on oceanic and atmospheric dynamics may arise from its role as a bridge connecting various oceanic regions.
To understand the importance of sea communities in outgoing heat transfer, we analyzed the outbound eigenvector centrality. Fig. 5 highlights the key communities using outbound eigenvector centrality in the oceanic community network. Fig. 5a shows the outbound eigenvector centrality of each community with their interactions, calculated using average weights. This approach allows us to determine which communities are most influential in transmitting heat flows to other parts of the network. Considering the measurement’s characteristic, one can see that communities 7, 2, and 8 have high influence to the system in terms of their outgoing heat transfer. These communities are related to a diffuse community spread across the globe, primarily in the Indian and Atlantic Oceans, with partial coverage in the Pacific Ocean, indicating the importance of these oceanic systems in heat transfer (Fig. 5b).
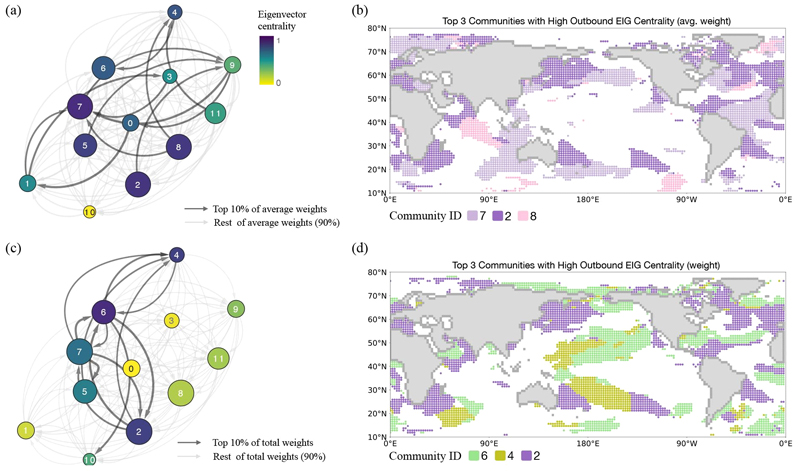
Identification of key communities using outbound eigenvector centrality in the network of communities. (a, c) Networks illustrate outbound eigenvector centrality using average weights and total weights, respectively, with node colors representing the centrality values. The top 10% of average weights are highlighted in darker grey. (b, d) The top 3 communities based on the outbound eigenvector centrality from (a), and (c) are shown. The node size is determined based on the number of links, both incoming and outgoing.
In Fig. 5c, outbound eigenvector centrality was recalculated using total weights, providing insight into each oceanic community's comprehensive influence when considering all outgoing connections. The nodes are colored according to their recalculated centrality values, revealing how different regions contribute to the overall heat flow in the ocean. In the network with total weights shown in Fig. 5c, the communities with high outbound eigenvector centrality are communities 6, 4, and 2 (Fig. 5d). These communities consist of two types of regional characteristics: two communities (communities 6 and 4) are close to the ENSO system, while another community (community 2) represents a more dispersed community around the globe, with stronger connections to the North Atlantic Ocean. This suggests that the North Atlantic Ocean and the outer part of the ENSO system may play a primary role in distributing heat flows throughout the oceanic system.
Examining the flow directions between these communities through Figs. 5c, it appears that community 6 directs its flow towards community 2 and 7, which are located near the ENSO system and also spread across the entire system. The fact that the community 11, representing the main parts of the ENSO system, does not rank high in outbound eigenvector centrality again suggests that its functional role may lie in bridging other oceanic regions, with the main outgoing flows likely originating from other oceanic regions near the ENSO system.
In contrast to the previous analysis, inbound eigenvector centrality can highlight important sea regions in terms of their incoming flows, and Fig. 6 depicts the key communities by applying inbound eigenvector centrality within the oceanic community network. Panels (a) and (c) illustrate the inbound eigenvector centrality of each community, calculated using average weights and total weights, respectively. In panel (a), the average weights were used to determine which communities receive the most influence from their connected nodes, with nodes colored based on their centrality values. Communities with the highest inbound influence, such as communities 2, 6, and 7, are primarily associated with parts of the North Pole, the periphery of ENSO region, and the Atlantic Ocean, suggesting that these areas can play a major role in receiving and concentrating heat flows from other regions, considering their weight per unit link.
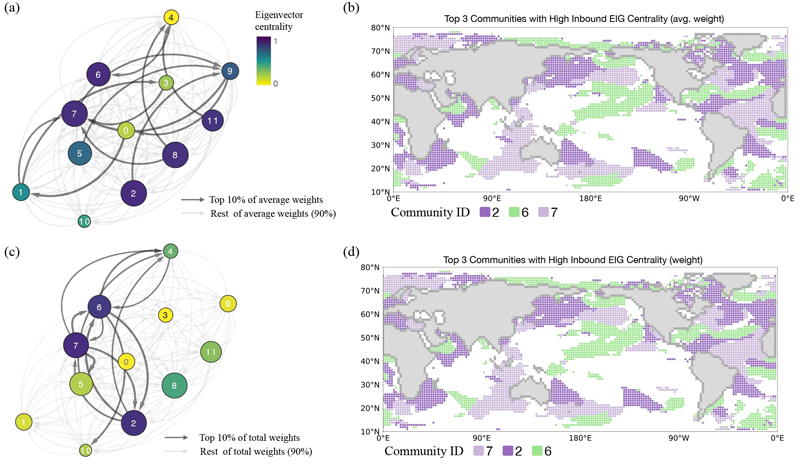
Identification of key communities using inbound eigenvector centrality in the network of communities. (a, c) Networks illustrate inbound eigenvector centrality using average weights and total weights, respectively, with node colors representing the centrality values. The top 10% of average weights are highlighted in darker grey. (b, d) The top 3 communities based on inbound eigenvector centrality from (a), and (c) are shown. The node size is determined based on the number of links, both incoming and outgoing.
In panel (c), inbound eigenvector centrality was recalculated using total weights to provide a broader understanding of the influence each community receives when considering the overall strength of all incoming connections. Communities with high inbound centrality in this analysis are more comprehensively linked, revealing which parts of the oceanic system act as major recipients of heat flows. The analysis shows that communities 7, 2, and 6 exhibit high inbound eigenvector centrality, with most of these communities being widely distributed across the Atlantic and the near ENSO regions. One can notice that these key communities are the same as those identified by inbound eigenvector centrality with average weights, as shown in Figs. a and b, with only the order of the top communities being different. In particular, the reciprocal relationship between community 6 and 7 in Fig. 6d can be crucial, as this mutual heat transfer involves the Indian Ocean, the Atlantic Ocean, and the peripheral regions of the ENSO system as major contributors to heat accumulation, driven by connections from various oceanic sources. Especially, the composition of communities 2 and 7 requires further study, as they include three oceanic regions within the same community, which may exhibit synchronous heat dynamics. Given that previous studies have reported the crucial role of interactions between the Indian and Atlantic Oceans in ocean warming, along with a partial role of the Pacific Ocean (Yang et al., 2022), these alignments of major inbound eigenvector centrality for key oceanic regions suggest that the global oceanic heat transfer network analyzed in this study could provide valuable insights into the functional roles of oceanic regions within the context of their interactions.
3.5. Functional Roles of Key Sea Regions
Fig. 7a focuses on the community network encompassing major oceanic regions—ENSO (community 11), Indian (community 8) and Atlantic Ocean (community 7), and the periphery of the ENSO system (community 6 and 9). The bidirectional links between these communities represent their mutual interactions (total weights), with asymmetric weights on the relationships highlighted through distinct color. Red arrows indicate links where one direction has significantly stronger influence—at least 1.5 times greater than the other—while the strongest mutual links are highlighted in light blue. The results underscore the complex interplay among these regions, particularly emphasizing the dominant influences from the main ENSO system (community 11) to the periphery of the ENSO system (community 9), from the Indian Ocean (community 8) to the Atlantic Ocean (community 7), and from the Atlantic Ocean (community 7) to the periphery regions of the ENSO system (community 6). In addition to these connections, interactions between communities 6 (peripheral regions of the ENSO system) and 11 (the main parts of the ENSO system) maintain strong mutual influences. These major connections demonstrate the strong correlations among the ENSO, Atlantic, and Indian Oceans, suggesting that these ocean regions act as critical hubs for balancing heat exchanges, with significant asymmetric influences involving the ENSO system and Indian Ocean.
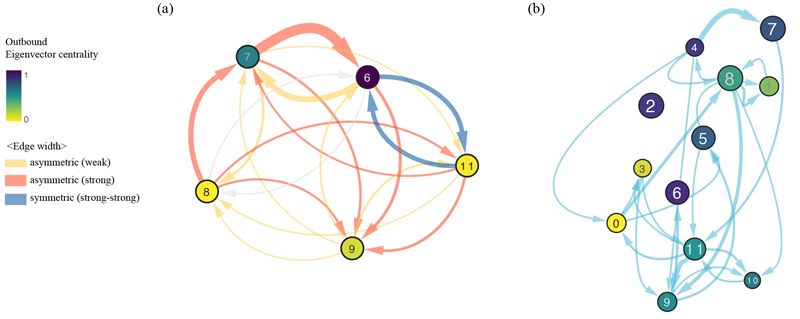
Functional roles of major sea regions in community networks. (a) Five communities representing five ocean regions are extracted from sea community network with total weights: 6 (ENSO), 7 (Indian and Atlantic Oceans), 8 (Indian Ocean), 9 (Indian and ENSO), and 11 (ENSO). Each pair of nodes has bidirectional links, and links with asymmetric weights are highlighted with different colors. A link with a stronger weight that is at least 1.5 times greater than the weaker link’s weight is shown in red (weaker is in orange). The strongest bidirectional links are colored in light blue. (b) Edges with the top 10% edge betweenness values (ranges from 0 to 0.44) are displayed. A hierarchical layout from Cytoscape is used, with node colors and sizes are based on outbound eigenvector centrality. The node size is determined based on the number of links, both incoming and outgoing.
Fig. 7b provides a deeper examination of the network by identifying edges with the top 10% edge betweenness values, representing the most significant pathways within the oceanic community network. The nodes are colored based on their outbound eigenvector centrality, and the layout is constructed using the hierarchical algorithm in Cytoscape, illustrating the heat flow among communities from top to bottom in the heat transfer network. The high edge betweenness values indicate the primary shortest paths that facilitate major heat exchanges between different ocean regions. When we extract the edges with high edge betweenness, communities 4 (mostly in the Pacific Ocean), 7 (distributed in the Indian, Pacific, and the North Atlantic Ocean), and 8 (mainly in the Indian Ocean) are particularly prominent, suggesting their roles as essential conduits for thermal energy transfer. The hierarchical layout used in this visualization further clarifies the network structure, emphasizing how regions like the peripheral areas of the ENSO system (e.g., community 9, 1, and 6), which link multiple major basins, act as central nodes in the oceanic heat transfer network. These findings suggest that the outer parts of the ENSO system and diffusive oceanic communities (e.g., community 4, 7, and 9) not only accumulate heat but also play a crucial role in redistributing it globally, thereby contributing significantly to the regulation of global oceanic temperatures.
4. Conclusions and Discussions
In this study, we applied the heat equation approach to gain a comprehensive understanding of the complex oceanic heat transfer network and the functional roles of various oceanic regions. Since the heat equation approach provides directional and weighted flows between regions, it allows for the examination of the spatial distribution of inward and outward heat flows through these informative interactions, highlighting regions with significant heat transfer activity such as the ENSO system and the North Atlantic Warming Hole (NAWH). To capture high-level regional interactions, we extracted the backbone network structure and performed community detection, identifying key oceanic communities and their interconnections. By focusing on previously reported interactions between key oceanic regions in ocean warming, betweenness centrality and outbound/inbound eigenvector centrality analyses highlighted critical pathways and influential regional nodes within the network. In particular, the communities linked to the ENSO system and polar areas appear to play a critical bridging role in the heat transfer network. The periphery of ENSO system also conducts an important role in terms of the inbound and outbound eigenvector centrality. The strong relationships among key oceanic communities of the ENSO system, the Indian Ocean, and the Atlantic Ocean were further analyzed in an extracted network, demonstrating that the regions serve as crucial hubs for both accumulating and redistributing heat with their mutual interactions. These findings collectively underscore the functional roles of major oceanic regions, such as the ENSO system, Indian Ocean, and polar areas, in facilitating global heat transfer, maintaining oceanic temperature dynamics, and contributing to climate stability through their complex interactions.
However, the community detection in this study could be improved, as detecting communities in directed networks is inherently complex due to the separation of source and target nodes (Leicht et al., 2008; Kim et al., 2010). Considering this, the current methodology could be further enhanced, with this study serving as an initial step toward testing the validity of the complex systems approach in understanding relationships between sea regions based on SST correlations. This work may also provide a new perspective for analyzing complex climate interactions.
Acknowledgments
This research was supported by Global - Learning & Academic research institution for Master’s·PhD students, and Postdocs (LAMP) Program of the National Research Foundation of Korea (NRF) grant funded by the Ministry of Education (No. RS-2023-00301702). We appreciate the productive discussion with Prof. Mi Jin Lee at Hanyang University.
References
-
Blondel, V.D., Guillaume, J.L., Lambiotte, R. and Lefebvre, E., 2008, Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, P10008.
[https://doi.org/10.1088/1742-5468/2008/10/P10008]

-
Boers, N., Goswami, B., Rheinwalt, A., Bookhagen, B., Hoskins, B. and Kurths, J., 2019, Complex networks reveal global pattern of extreme-rainfall teleconnections. Nature, 566, 373-377.
[https://doi.org/10.1038/s41586-018-0872-x]

-
Bonacich, P., 1972, Factoring and weighting approaches to status scores and clique identification. Journal of Mathematical Sociology, 2, 113-120.
[https://doi.org/10.1080/0022250X.1972.9989806]

-
Brandes, U., 2008, On variants of shortest-path betweenness centrality and their generic computation. Social Networks, 30, 136-145.
[https://doi.org/10.1016/j.socnet.2007.11.001]

- Clement, A.C., Goes, L.M., Cane, M.A. and Klavans, J.M., 2018, Testing the role of the ocean in historical simulations of Atlantic multidecadal variability and the North Atlantic warming hole. AGU Fall Meeting, A54C-09.
-
Deser, C., Alexander, M.A., Xie, S.P. and Phillips, A.S., 2010, Sea surface temperature variability, Patterns and mechanisms. Annual Review of Marine Science, 2, 115-143.
[https://doi.org/10.1146/annurev-marine-120408-151453]

- Dugué, N. and Perez, A., 2015, Directed Louvain: Maximizing modularity in directed networks: Research Report. Université d'Orléans, (hal-01231784).
-
Freeman, L.C., 1977, A set of measures of centrality based on betweenness. Sociometry, 40, 35-41.
[https://doi.org/10.2307/3033543]

-
Hu, S. and Fedorov, A.V., 2020, Indian Ocean warming as a driver of the North Atlantic warming hole. Nature Communications, 11, 4785.
[https://doi.org/10.1038/s41467-020-18522-5]

-
Josey, S.A., De Jong, M.F., Oltmanns, M., Moore, G.K. and Weller, R.A., 2019, Extreme variability in Irminger Sea winter heat loss revealed by Ocean Observatories Initiative mooring and the ERA5 reanalysis. Geophysical Research Letters, 46, 293-302.
[https://doi.org/10.1029/2018GL080956]

-
Kim, Y., Son, S.-W. and Jeong, H., 2010, Large-scale quantitative analysis of painting arts. Physical Review E, 81, 016103.
[https://doi.org/10.1103/PhysRevE.81.016103]

-
Lapointe, F., Bradley, R.S., Francus, P., Balascio, N.L., Abbott, M.B., Stoner, J.S., St-Onge, G., De Coninck, A. and Labarre, T., 2020, Annually resolved Atlantic sea surface temperature variability over the past 2,900 years. Proceedings of the National Academy of Sciences, 117, 27171-27178.
[https://doi.org/10.1073/pnas.2014166117]

-
Leicht, E.A. and Newman, M.E.J., 2008, Community structure in directed networks. Physical Review Letters, 100, 118703.
[https://doi.org/10.1103/PhysRevLett.100.118703]

- Lozier, S., Li, L. and Li, F., 2019, The North Atlantic "Cold Blob": An alternate explanation. EGU General Assembly, 21, 1 p.
-
McPhaden, M.J., Zebiak, S.E. and Glantz, M.H., 2006, ENSO as an integrating concept in Earth science. Science, 314, 1740-1745.
[https://doi.org/10.1126/science.1132588]

-
Newman, M.E.J., 2018, Networks (2nd ed.). Oxford University Press.
[https://doi.org/10.1093/oso/9780198805090.001.0001]

- NOAA Office of Satellite and Product Operations, 2024, Sea Surface Temperature (SST). Retrieved from https://www.ospo.noaa.gov/products/ocean/sst.html, (accessed March, 2024).
-
Peng, Q., Xie, S.-P., Passalacqua, G.A., Miyamoto, A. and Deser, C., 2024, The 2023 extreme coastal El Niño: Atmospheric and air-sea coupling mechanisms. Science Advances, 10, eadk8646.
[https://doi.org/10.1126/sciadv.adk8646]

-
Robertson, A.W., Mechoso, C.R. and Kim, Y., 2000, The influence of Atlantic sea surface temperature anomalies on the North Atlantic Oscillation. Journal of Climate, 13, 122-138.
[https://doi.org/10.1175/1520-0442(2000)013<0122>2.0.CO;2]

-
Serrano, M.Á., Boguñá, M. and Vespignani, A., 2009, Extracting the multiscale backbone of complex weighted networks. Proceedings of the National Academy of Sciences, 106, 6483-6488.
[https://doi.org/10.1073/pnas.0808904106]

-
Yang, Y.M., Park, J.H., An, S.I. and Kim, S.K., 2022, Increased Indian Ocean-North Atlantic Ocean warming chain under greenhouse warming. Nature Communications, 13, 3978.
[https://doi.org/10.1038/s41467-022-31676-8]

