연속강우 시나리오와 물리기반 모형을 연계한 얕은 산사태 위험지도 구축

1. 서 론

우리나라 총 면적의 약 70%는 산지지형으로 이루어졌으며, 본 지역의 자연사면에는 화강암 또는 편마암의 풍화로 인하여 형성된 2 m 이하의 얕은 토층이 상부에 위치하고 있다(Kim and Song, 2015). 이로 인하여 우리나라는 매년 우기철에 오랜 과거부터 필연적으로 지속적인 다양한 규모와 형태의 산사태 피해를 입어왔다. 최근에는 전지구적인 기후변화로 인해 많은 연구자들은 국내의 여름철 국지성 집중호우 또는 폭우의 강도와 빈도수가 증가하는 경향을 분석하여 보고하고 있다(Choi, G. et al., 2008; Choi, K.S. et al., 2010; Choi, Y. et al., 2011; Jung et al., 2011; Lee et al., 2011; National Institute of Meteorological Research, 2012). 이러한 기후변화 추세는 국내 기존의 대표적인 산사태 발생 유형을 변화시켰고, 뿐만 아니라 발생 빈도와 규모 또한 증가시켰다. 한편, 그와 동시에 국내 도심지 확장 및 거주지 개발이 지속적으로 산지지역까지 확장됨에 따라, 산사태로 인한 인적, 물적 피해는 급증하기 시작하였다. 산림청(Landslide Damage Status, 2022)에 따르면, 최근 10년간(2010-2019) 산사태로 인한 피해면적은 2,264 ha, 인명피해(사망자 수)는 53명, 피해복구비는 4,389억원이며 2000년도 근방을 전후로 급격히 규모가 증가하고 있는 추세다.

이와 같이 재해 규모가 매년 급증하는 추세 속에서, 재해 관리자 또는 대응 결정권자에게 신뢰성 있고 정확한 예측정보를 제공할 수 있는 기술이 시급하게 요구되는 상황이다. 특히, 2011년 서울 우면산 산사태와 같이 도심지역에서 발생되는 산사태의 경우 도시생활권의 인구밀집적인 토지이용으로 인하여 사방구조물 대책만으로는 인명피해를 저감하기에 부족한 실정이다. 따라서, 강우특성에 따라 산사태 고위험지역을 선별하여 선제적 대응 및 대피 활동에 근거자료로 적용할 수 있고, 장기적으로는 토지이용 및 도시개발 계획에 활용할 수 있는 산사태 위험지도 구축이 필요하다.

산사태 방재분야의 선진국인 미국, 일본, 대만, 이탈리아 등에서는 과거의 산사태 이력 및 강우자료를 기반으로 경험적 또는 확률론적 기준을 제시하고, 이를 산사태 위험성 판단에 활용하여 왔다. 가장 대표적인 경우로 Caine (1980)과 Guzzetti et al. (2008)이 제시한 I-D 곡선이 있다. 과거의 산사태 유발 강우자료들을 분석하여 강우강도(Intensity)와 지속시간(Duration) 간의 상관관계를 도출하고 산사태를 유발하는 강우 한계선을 선정한다. 그러나 이러한 과거 산사태 이력자료와 강우자료를 기반으로 선정된 확률론적 위험도 평가기술은, 1) 지질, 지반, 지형과 같은 지역특성을 고려한 공간 예측 성능이 부족한 점과, 2) 산사태 발생에 대한 물리적 메커니즘의 근거를 제시하지 못하며, 3) 이력자료에 대한 의존성으로 인하여 이력자료가 없거나 부족한 지역을 대상으로는 예측 신뢰성을 보장하지 못하는 한계점이 있다.

한편, 물리이론을 통해 산사태 발생 메커니즘의 수학적 해를 계산하는 산사태 물리모형을 적용하여 강우에 따라 산사태 위험성을 평가하는 다양한 연구가 진행되고 있다. 특히, GIS (Geographic Information System) 기술이 연계되기 시작하면서, 물리기반 평가모형들의 적용범위가 확장됨에 따라 광역지역의 자연사면을 대상으로 한 다양한 무한사면 안정해석 모델들이 제시되어 왔다(Wu and Sidle, 1995; Montrasio, 2000; van Beek, 2002; Baum et al., 2008; Simoni et al., 2008). 그러나 실시간 강우에 따른 산사태 위험성 예측에 물리모형을 적용하는 경우, 해석시간 및 전산부담의 문제가 발생한다. 즉 모델이 정교화되고 대상지역이 확장될수록 위험도를 산출하기 위한 소요시간이 증가하며, 이는 실시간 강우변화에 따른 반복적인 해석을 어렵게 하며 대응 및 대피를 위한 골든타임 확보에 문제를 만든다.

따라서, 궁극적으로 물리모형을 광역적인 산사태 위험성 예측에 실용화하기 위해서는 강우 시나리오에 따라 해석 산출결과 지도를 미리 구축하는 방향으로 국내외 연구가 진행될 수밖에 없다고 판단된다. 이에 대한 일환으로, 본 연구에서는 세 개의 연구대상지역에 대하여 연속강우 시나리오에 따라 물리모형을 적용하여 산사태위험지도를 작성하였으며, 작성된 지도의 활용성을 고찰하고, 한계점 및 후속연구의 필요성을 논의하였다. 이를 위해, 기존의 경험적 통계기반의 강우기준이 아닌, 강우 침투해석을 바탕으로 산출한 각 지역 고유의 위험 연속강우량들을 강우 시나리오로 활용하였다. 또한, 물리모형 해석을 위해 필요한 각 지역의 토심, 지형, 지반수리역학 특성, 초기조건 등에 대한 지료들의 구축방법들을 상술하였다.

2. 이론적 배경

2.1 연속강우량 정의

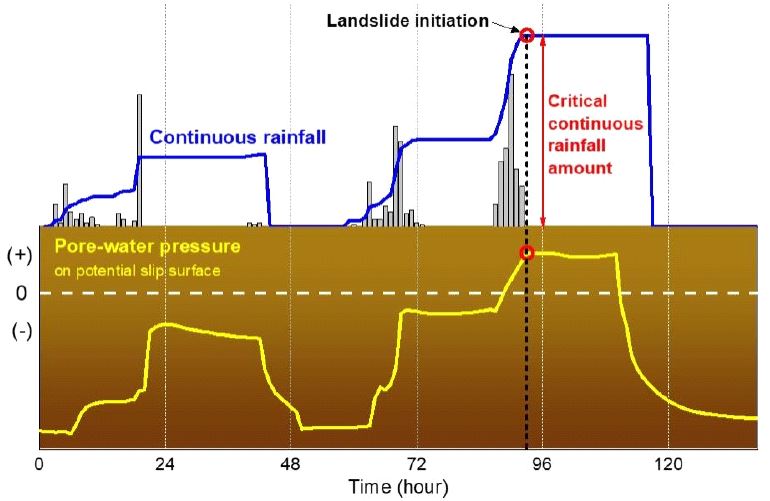
임계연속강우량은 자연사면이 산사태가 발생할 수 있는 역학적 불안정 상태로 진입하기 위해 필요한 최소 연속강우량으로 정의되며, 개별 자연사면은 각각의 고유 지질, 지형, 지반공학 특성을 내재하고 있으므로 자연사면은 개별적으로 고유의 임계연속강우량을 내재하고 있다(Park et al., 2020). 이 정의는 연속강우와 산사태에 대한 과거기록들에 대한 관찰을 통해 착안되었다. 그림 1은 연속강우량 및 임계연속강우량의 개념을 설명하는 다이어그램이다. 임계연속강우량은 얕은 산사태(shallow landslide) 유형에 적합한 규준이며, 그 이유는 다음과 같다. 연속강우량의 개념은 지반에 침투되는 강우가 사면포화도의 지속적 증가에 기여하는 개념이며 연속강우 기간 동안의 배수효과는 미미하다고 전제하고 있다. 따라서, 연속강우의 기간이 길어질수록 배수로 인한 강우유출 효과가 커지므로, 강우가 장기간 연속될수록 연속강우량은 사면의 습윤도를 과대평가하는 경향을 가지게 된다. 그러나, 짧게는 수 시간에서 길게는 약 2일 정도의 단기간 동안 높은 강도로 집중되는 최근의 호우특성을 고려하였을 때, 연속강우 기간 동안 배수효과로 인한 지중 강우침투수의 유출량은 미미함을 추론할 수 있으며, 이는 자연사면에 대한 장기 모니터링 연구를 통해서도 검증된 바 있다(Kim et al., 2021).

Fig. 1.

Conceptual diagram of critical amount of continuous rainfall.

연속강우가 지속되는 동안 지표에서의 폰딩(ponding) 또는 지표유출 없이 모든 강우가 침투된다면 연속강우량은 사면의 습윤도 및 불안정성에 대한 이상적이고 직접적인 지표가 될 수 있다. 그러나 실제 현장조건에서는 높은 강우강도의 범위가 10~100 mm/h정도이고 이를 환산하면 2.8×10^-6~2.8×10^-5 m/s에 해당된다. 이는 일반적으로 모래질 흙의 포화투수계수 범위에 속한다. 따라서, 점토질이 우세한 지반의 경우에는 실제 높은 강도의 강우가 내리는 경우 일부는 지반으로 침투되지 못하고 지표유출이 발생될 것임을 추론할 수 있다. 그 결과, 해당지역에서 지표로서의 연속강우량은 실제 사면의 습윤도를 과대평가하는 경향이 있을 수 있다. 그러나, 산지지역의 기반암을 덮고 있는 풍화토층은 사질토에 속하므로, 토층의 포화투수계수가 높은 강우강도와 비슷하거나 크게 작지 않다. 따라서, 강우가 높은 강도로 지표에 접촉하더라도 폰딩 또는 지표유출로 인한 손실량이 크지 않을 것임을 추측할 수 있다. 또한, 산사태 위험성을 조기에 판단하고 경보를 내리기 위한 목적을 고려하였을 때, “모든 강우가 손실 없이 지중에 침투 및 저류되어 사면포화도 증가에 기여한다”는 보수적인 가정 및 모형설계는 필수적이라고 판단된다.

2.2 산사태 물리기반 모형

우리나라의 자연사면에서 강우시 발생되는 얕은 표층파괴(shallow landslide)를 해석하기 위하여 물리기반의 산사태 예측모형을 개발하였다. 지속적인 강우시 자연사면 토층내 우수침투로 습윤영역(wetting zone)이 아래로 확대되어 토층의 하중으로 인한 활동력 증가 및 토층 내 흙입자간의 결합력 감소로 산사태가 발생하게 된다. 이와 같은 강우시 얕은 표층파괴 발생 메카니즘을 토대로 지표수의 침투 발생, 지중침투 우수의 흐름으로 인한 습윤영역(wetting zone)의 확대, 그리고 포화로 인한 토층의 활동력 증가 및 토층내 흙입자간의 결합력 감소로 이어지는 일련의 산사태 발생 프로세스를 구분하여 해석모델을 개발하였다.

그림 2a는 강우시 지표수의 유출과 강우의 침투, 이를 고려한 무한사면의 안정성을 평가하기 위한 모식도이다. 강우시 우수는 지중침투 뿐만아니라 지표유출이 동시에 발생하게 되므로 지표수와 지하수에 대한 일체적인 유동해석을 적용하고, 불포화 토층내에서의 지하수 유동에 대한 물-공기의 2-phase flow 해석과 흡입응력을 고려한 무한사면의 안정해석을 활용하였다. 따라서 본 연구에서 개발된 우리나라 자연사면에 적합한 물리기반 산사태 예측모형은 그림 2b에서 보는 바와 같이 3가지 해석기법 즉, 지표침투해석(surface water flow and infiltration), 지중흐름해석(Fluid flow in subsurface) 및 흡입응력을 고려한 무한사면안정해석(Infinite slope stability analysis considering suction stress)을 융합하여 개발하였다.

Fig. 2.

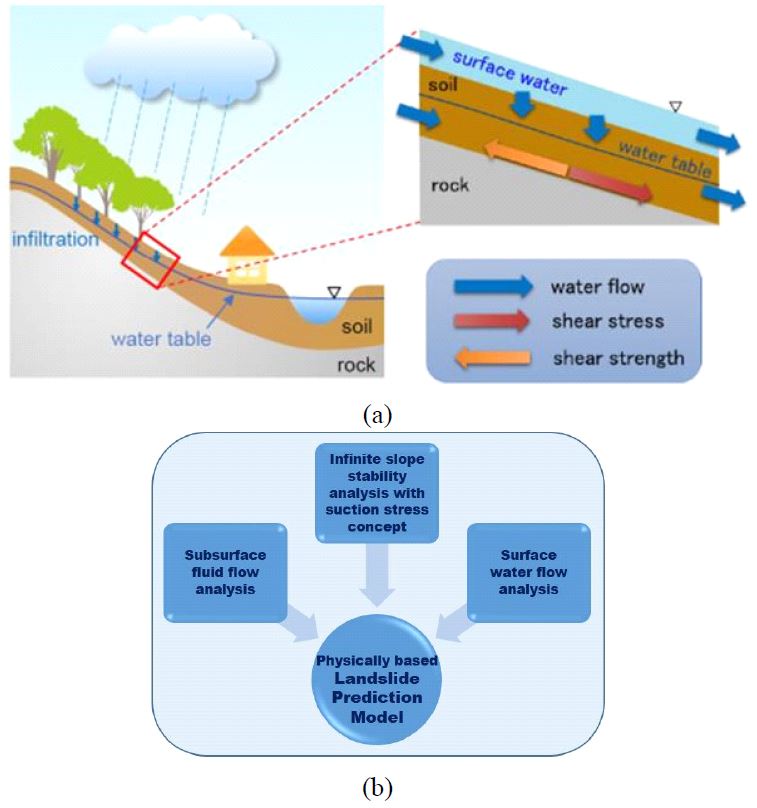
(a) Rainfall-induced shallow landslide mechanism and (b) conceptual diagram of physically based landslide prediction model.

먼저 강우침투수의 지중흐름과 관련해서, 토층(p)이 얕은 지반에서 지하수 유동은 물-공기의 2-Phase Flow이므로 연속방정식은 다음과 같다.

$$

(1)

여기서, ρ_p는 토층 p에서의 밀도[kg/m³], φ는 간극율, S_p는 토층 p에서의 포화도, t는 시간[s], F_p는 토층 p에서의 유량[kg/m²/s], ρ_pq_p는 토층 p에서의 유량증가속도[kg/m³/s], 아래첨자 p의 w는 물, g는 공기를 나타내며, 유량은 다음 식으로 얻을 수 있다.

$$

(2)

여기서, u_p는 토층 p에서의 Darcy속도[m/s], k는 지반의 절대침투율[m²], k_rp는 토층 p에 대한 상대침투율, μ_p는 토층 p의 점성계수[Pa·s], P_p는 토층 p의 압력[Pa], g는 중력가속도[m/s²]를 나타낸다.

둘째로 강우의 지표흐름과 관련해서, 천수류를 가정한 2차원 지표수흐름을 고려하였으며, 이는 다음과 같은 연속방정식으로 나타낼 수 있다.

$$

(3)

여기서, h_s는 수심[m], v는 평균유속[m/s], q는 지하수의 침투 혹은 강수 등에 의한 유입유량[m/s]을 나타낸다. 확산 근사식을 적용하여 i_g의 경사를 갖는 1차원 수로에서의 운동방정식은 아래와 같다.

$$

(4)

여기서 i_g는 수로의 경사(=∂z/∂x), n은 Manning의 조도계수, R은 평균수심[m] 이다. 식 4를 v에 대해서 풀면 최종적으로 다음 식을 구할 수 있다.

$$

(5)

이를 선형화 확산근사모형이라고 하며 Kinematic wave모형과 확산근사모형의 중간에 해당한다. 자연상태에서의 일반적인 물의 흐름에 대해서는 이 근사식이 대부분의 경우에 유효하며, 안정성이 우수하고 확산에 대한 해와 거의 일치함을 알 수 있다.

셋째로 흡입응력을 고려한 무한사면 안정해석과 관련해서, 토층의 심도가 일정하고 균일한 흙으로 형성되었음을 가정하였다. 흙요소 저면에서 파괴면에 작용하는 전단강도는 Coulomb의 파괴기준에 따르면 식 6과 같이 나타낼 수 있다.

$$

(6)

여기서, c는 점착력[N/m²], σ_n′은 유효응력[N/m²], φ는 내부마찰각이다. 유효응력의 경우 Lu and Likos (2006)에 의해 제안된 포화 및 불포화상태를 모두 고려할 수 있는 수식을 활용하였다(식 7).

$$

(7)

여기서, σ^S는 흡입응력[N/m²]이다. 흡입응력은 토층의 포화도에 따라서 다음과 같이 구할 수 있다.

$$

(8)

$$

(9)

여기서, P_a는 간극 공기압[N/m²], P_w는 간극수압[N/m²], θ는 체적함수비, θ_S는 포화체적함수비, θ_r는 잔류체적함수비, S_we는 유효포화도이다. 토층이 포화상태일 경우 유효응력은 식 8을 식 7에 대입하여 구할 수 있다.

$$

(10)

이는 유효응력의 경우 연직응력보다 간극수압 만큼 작다는 것을 의미한다. 반면에, 토층이 불포화상태일 경우 식 9에서 σ^S는 음수이므로 식 7에 대입하면 유효응력은 연직응력보다 커지게 된다. 흡입응력은 흙입자의 접촉면과 그 주변에 작용하는 반데르발스(van der Waals) 힘, 전기이중층에 의한 정전기력, 표면장력 등 국소적인 힘들을 거시적인 개념의 힘으로 정리한 것이다. Lu and Godt (2008)의 유도식에 따르면, 불포화 흡입응력을 적용한 무한사면의 흙요소 저면 사면안전율 F_S는 전단활동력 S에 대한 전단저항력 R의 비로 표현되며, 다음 식과 같이 구할 수 있다.

$$

(11)

여기서, γ_t는 습윤단위체적중량[N/m³], β는 사면경사, H는 전단면까지의 토층두께이다. 위 식에서 첫 번째 항은 내부마찰각, 두 번째 항은 점착력, 세 번째 항은 흡입응력에 대한 식으로 구분할 수 있다.

3. 데이터 구축

3.1 연구대상지역

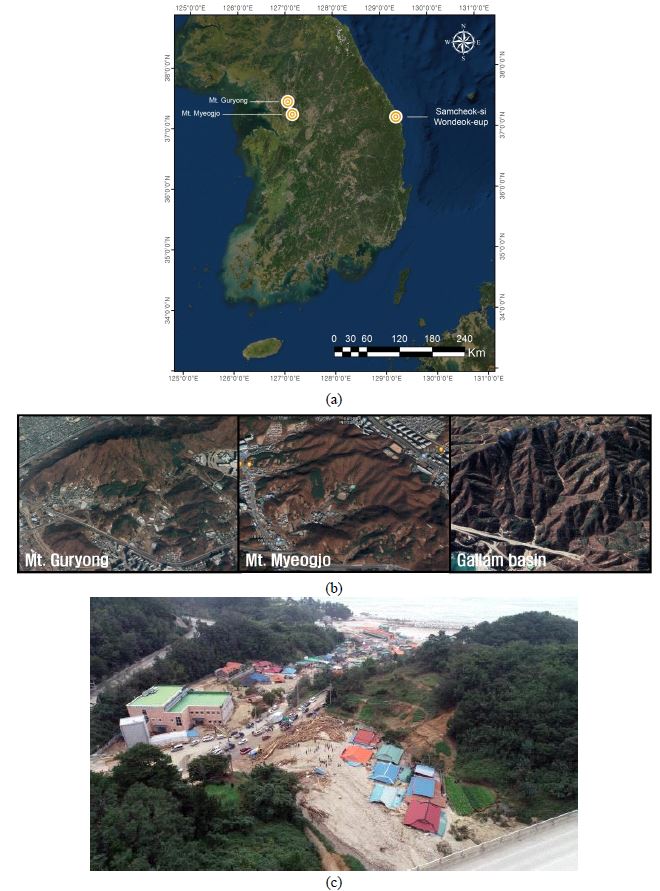
본 연구에서는 물리기반 산사태 예측모형과 연속강우량 시나리오를 이용하여 산사태 위험지도를 작성하고자 한다. 산사태 위험지도를 작성하기 위한 연구대상지역은 서울, 경기 및 강원지역에 각각 1개소로 선정하였으며, 표 1 및 그림 3a는 연구대상지역의 위치와 특징을 나타낸 것이다. 또한, 그림 3b는 각 연구대상지역의 항공사진 자료를 나열하고 있다. 서울지역의 경우 서초구에 호상흑운모 편마암 지질조건을 가진 구룡산 일대를 대상으로 선정하였고, 경기지역의 경우 용인시에 반상변정 편마암 지질조건을 가진 멱조산 일대를 대상으로 선정하였다. 이 두지역의 경우 현재 국립산림과학원에서 운영하는 산사태 모니터링시스템이 운영되고 있다. 국립산림과학원에 따르면, 구룡산에서는 2010년 9월 21일 18시 경에 다수의 산사태 피해가 기록된 바 있으며, 멱조산에서는 지금까지 특별한 산사태 발생이 보고된 바 없다. 그리고 강원지역의 경우 삼척시에 우백질 화강암 지질조건으로 이루어진 갈남리 산림유역을 대상으로 선정하였으며, 이 지역은 2019년 여름철 집중호우(태풍 ‘미탁’)로 인하여 10월 2일 23시-24시 경에 다수의 산사태 및 토석류가 발생하여 신남마을 일대에 피해가 발생한 지역이다(그림 3c).

Table 1.

Summary of study areas.

Fig. 3.

(a) Locations and (b) aerial photographs of study areas, and (c) a village damaged by landslides and debris flows transported from Gallam basin in 2019.

3.2 입력인자 데이터 구축

3.2.1 지형 및 토심

물리기반 예측모형을 이용하여 산사태 위험지도를 작성하기 위해서는 연구 대상지역에 대한 수치표고모형(Digital elevation model; DEM) 자료를 활용하여 지형 및 토심자료를 구축해야 한다. 본 연구에서 사용된 DEM자료는 10 m×10 m의 메쉬 크기로 지형자료 및 고도의 자료를 구축하였다. 연구지역에 대한 토심을 산정하기 위하여 현장조사 결과와 경사도 기반의 토심 추정모델인 S-model (Saulnier et al., 1997)을 적용하였다. 그림 4는 각 연구대상지역의 사면경사 분포와 3개 토심등급 분포를 보여주고 있다. 구룡산과 멱조산 일대는 대부분의 지역이 사면경사 40° 이하를 띠고 있는 반면, 갈남리 유역 일대는 40° 이상의 가파른 지형이 다수 분포하고 있음을 확인할 수 있다. 한편 토심등급이란, S-model을 기반으로 추정된 토심분포를 3개의 등급으로 분류한 결과를 뜻한다. 즉, 토심을 1 m 이하, 1 m 초과 및 2 m 이하, 2 m 초과와 같이 3개 구간으로 나누어 지역별 토심에 따라 등급을 분류하였다. 토심 2 m를 초과하는 지역은 대부분 평탄한 산지하부 퇴적지역에 속하며, 산사태 또는 토석류가 시작되는 산지 상부지역은 토심이 1 m 이하가 지배적임을 확인할 수 있다.

Fig. 4.

Distributed slope angles and classfied soil-depth areas of (a) Mt. Guryong, (b) Mt. Myeogjo, and (c) Gallam basin.

3.2.2 지반 수리역학 특성

물리모형을 이용한 산사태 예측해석을 위해서는, 현장 고유의 기초토질 물성 및 불포화토 특성 자료들이 요구된다. 먼저 단위중량, 전단강도 특성, 포화투수계수와 같이 기초토질 물성과 관련해서, 구룡산 및 멱조산 일대에서는 토질시료를 채취하여 관련 실내시험을 수행하였으며, 갈남리 유역에 대해서는 Kim et al. (2010)의 연구보고서에서 해당지역을 대상으로 조사된 결과자료를 활용하였다. 표 2는 각 연구대상지역의 기초토질 물성 입력자료들을 구축한 결과를 요약하고 있다. 이 중, 흙의 전단강도 특성에 해당하는 내부마찰각 외에 점착력 값은 모두 0 kPa로 설정하였다. 그 이유는, 국내 대부분의 산지지역 토층은 포화시 유효점착력 크기가 미미한 풍화 사질토의 범주에 속하는 것을 고려하였을 때, 국내외의 타 산사태/사면안정해석 연구사례들(Cho and Lee, 2002; Cho, 2009; Rossi et al., 2013; Montrasio et al., 2014; Oh and Lu, 2015)과 같이 보수적인 해석을 위해 점착력 값을 무시하는 가정을 적용하였기 때문이다.

Table 2.

Basic soil properties of study areas.

다음으로 토층의 수리특성 또는 불포화 특성과 관련된 흙-함수특성곡선(soil-water characteristic curve; SWCC)과 관련해서, 구룡산 일대에서는 선행연구 문헌(Jeong et al., 2018)에서 해당지역 시료로 건조과정의 SWCC 시험을 수행한 결과값을 활용하였다. 한편, 멱조산 일대와 갈남리 유역에 대해서는 한국지질자원연구원에 구축된 자동 흙-함수특성곡선 시험장치(Song, 2014)를 이용하여 각 해당지역 시료로 건조과정의 SWCC 시험을 수행하여 결과값을 얻을 수 있었다. 그러나, 실제로 강우가 지중에 침투되어 포화되는 현상은 SWCC의 습윤과정에 더 적합하므로 해석시에도 습윤과정의 SWCC 자료가 필요하다(Yoon et al., 2022). 따라서, 1차적으로 획득한 SWCC 자료들은 건조과정에 대한 실험결과이므로 이를 기반으로 습윤과정에 대한 SWCC를 산정하여야 한다. Park et al. (2017)은 건조과정의 SWCC에 대한 곡선 맞춤계수들을 활용하여 이에 대응하는 습윤과정 SWCC 곡선 맞춤계수들을 산정하는 간편 추정법을 제시하였다. 따라서 본 연구에서는 Park et al. (2017)이 제안한 방법을 활용하여 습윤과정의 SWCC를 산정하였고, 이어서 이에 대응하는 불포화투수계수곡선을 도출하였다(Yoon et al., 2021). 표 3은 각 연구대상지역 토질시료에 대해 van Genuchten (1980) 모델 기반의 SWCC 곡선 맞춤계수들을 도출한 결과이다. 그림 5는 각 연구대상지역의 곡선맞춤계수들을 활용하여 건조 및 습윤과정에 대한 흙-함수특성곡선과 불포화투수계수곡선을 도시한 것이다.

Table 3.

Curve-fitting parameters of soil-water characteristic curves in study areas.

Fig. 5.

Soil-water charateristic curves and hydraulic conductivity functions at (a) Mt. Guryong, (b) Mt. Myeogjo, and (c) Gallam basin.

3.2.3 물리모형의 초기조건 설정

물리기반 예측모형을 적용한 산사태 위험지도 작성시 초기 지반조건을 현장특성과 대응하도록 조성하기 위하여 연구지역을 정상상태(steady state)로 만들어야 한다. 이를 위하여, 연구지역 인접 관측소의 30년 강우량 및 기온 데이터 취득, 월평균 강수량 및 월평균 기온 산정, 연평균 유효 강우강도 산정(증발산량 고려)으로 이어지는 일련의 계산절차를 밟았다. 표 4는 연구대상지역에 인접한 기상관측소 자료를 기반으로 도출한 유효 강우강도을 나타낸 것이다. 연구대상지역과 인접한 기상청 관측소들 중 방재기상관측소가 공간적으로 더 인접하게 분포하여 있으나, 장기간 동안 강우자료를 최대한 누락없이 수집하기 위하여 유인측정이 병행되는 종관기상관측소 자료를 기준으로 분석하였다. 연평균 유효 강우강도는 2.16-2.46 mm/day의 범위에 있는 것으로 나타났다. 이어서, 산정된 연평균 유효 강우강도를 이용하여 앞서 구축된 지형 및 토심자료, 지반자료를 입력하여 7년 동안 해석을 수행하였다. 7년 동안 해석을 수행한 이유는 연구지역의 지반조건이 정상상태에 도달하기까지 충분히 긴 시간을 확보하기 위해서이다. 이와 같은 해석을 수행한 결과를 토대로 연구 대상지역의 각 메쉬 별 유효포화도 및 간극수압 등을 산정할 수 있으며, 이를 초기치로 결정하였다.

Table 4.

Annually effective rainfall intensity derived from the nearest Korea Meteorological Administration (KMA)’s weather observatory to each study area.

4. 결과 및 논의

4.1 연속강우 시나리오 선정

4.1.1 임계연속강우량 산출 절차

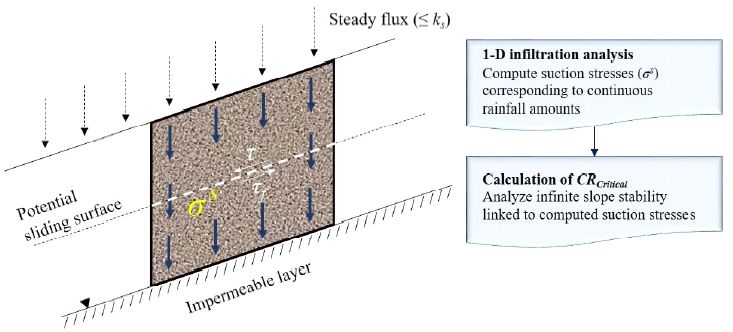
본 연구에서는 연속강우 시나리오에 기반한 산사태위험지도를 작성해야 하므로, 연구대상지역 특성에 맞는 유효한 강우시나리오를 선정해야 한다. 따라서, 지역특성 별로 산사태 발생에 위험한 임계연속강우량 범위 및 분포 등을 산출하기 위한 체계적인 해석 프로세스를 설계하였다(그림 6). 첫 번째는 누적된 연속 강우량에 따라 사면 내 잠재적 전단면(potential sliding surface)에서의 흡입응력(σ^S)을 계산하기 위해 특정 강우유량을 경계조건으로 하여 1차원 수치해석이 수행된다. 지표유출을 통한 강우손실을 방지하기 위해 강우유량은 토양의 최소 침투능(즉 포화투수계수, k_S)보다 낮게 설정된다. 각 대상 지역 별로 지반수리 특성 데이터셋의 종류와 토심조건을 고려하여 각각 개별적으로 침투해석을 수행한다. 두 번째는 이전 분석 단계에서 계산된 흡입응력을 연계하여 누적된 연속강우량에 대응하는 무한사면 안정성을 분석한다. 최종적으로 사면안전율(Factor of safety; FOS)이 1.0 이하가 되는 최소 연속강우량을 대상 사면에 대한 임계연속강우량으로 선정한다.

Fig. 6.

Analytical derivation process of critical amount of continuous rainfall.

4.1.2 연속강우 침투해석

연구대상지역에 대하여 누적되는 연속강우량에 따른 침투해석을 통하여 토층에서의 흡입응력 변화를 계산하도록 하였다. 이 과정은 유한요소해석 프로그램인 SEEP/W (GEO-SLOPE International Ltd., 2012)를 사용한 1차원 강우 침투의 수치해석을 기반으로 하고 있다. 즉, 주워진 지표면 유량(강우) 경계조건과 초기 압력수두 조건 등을 바탕으로, 비정상(transient) 조건의 각 타임 스텝에서 지배 방정식의 해를 구하는 과정을 통해 지반깊이별 압력수두의 변화가 계산된다. 지배 방정식(식 12)은 요소체적을 통과하는 흐름의 변화율이 요소체적 수분함량의 변화율과 같다는 기본개념을 포함하고 있다. 즉, 체적함수비 변화는 간극수압의 변화와 관련이 있기 때문에 식 13에 따라 더 낮은 구배(즉, 더 작은 m_w)를 가진 흙-함수특성곡선을 가진 지반 조건일수록 동일 강우 누적속도 또는 동일 요소체적 유량변화에 대해 간극수압이 더 크게 증가함을 의미한다.

$$

(12)

$$

(13)

여기서, H는 전체 수두(m), k_x와 k_y는 각각 x축 및 y축 방향으로의 투수계수(m/s), Q는 경계조건에 적용된 유량(m³/s), t는 시간(sec), m_w는 함수특성곡선의 구배, θ는 체적함수비, 그리고 u_w는 간극수압을 나타낸다.

기본적으로 1차원 토층기둥 형태로 해석 도메인을 설정하였으며, 연구대상지역의 경우 기반암까지 토심을 1 m, 1.5 m 및 2 m로 구분하였다. 모델링에 적용된 지반정수는 연구대상지역 별로 앞서 설명한 불포화 특성자료를 사용하였다. 초기조건은 토심에 관계없이 지하수위가 지표로부터 2 m 깊이에 위치하는 것으로 정상상태 해석을 수행하였다. 그 결과 초기시점에서는 지하수위에서 지표로 가까워질수록 음의 간극수압(모관흡수력)이 선형으로 증가하는 형태를 보인다. 측면 및 기반암 경계는 no flux 조건으로 지정되었으며 토층 기둥이 정수압 상태에 도달할 때까지 상부(지표면) 경계에는 1 mm/h의 일정한 유량(강우강도)을 적용했다. 본 경계조건은 연속강우량이 사면의 포화정도 또는 사면의 불안정성에 대한 직접적인 지표가 되도록 하는 이상적인 환경을 설정하기 위해 도출되었다. 여기서 이상적인 환경이란, 모든 빗물은 지표에서 폰딩이나 유출로 인한 물의 손실없이 지반으로 침투하여 토층의 포화도 증가와 사면 불안정성에 기여하는 환경이다. 그러기 위해서는 강우강도가 기본적으로 최소 침투능(즉, 포화투수계수)보다 작아야 한다. 그러나, 강우강도가 최소 침투능보다 작더라도 함수능이 큰 지반의 경우 해석 초기 지표 부근에 형성된 얕은 침윤전선의 하강속도가 느려 강우가 일시적으로 침투되지 못하는 경우가 생기기도 한다. 반대로, 극단적으로 낮은 강우강도는 지반 내에서 침윤전선이 형성되지 않고 기반암 바닥부터 지하수위가 상승하는 비현실적인 침투형태를 띤다. 따라서, 시행착오(trial and error)의 반복적인 해석과정을 통해, 해석 전체시간 동안 폰딩이나 지표유출을 유발하지 않는 범위 내에서의 보수적인 강우강도를 찾고자 하였고, 최종적으로 1 mm/h로 결정되었다.

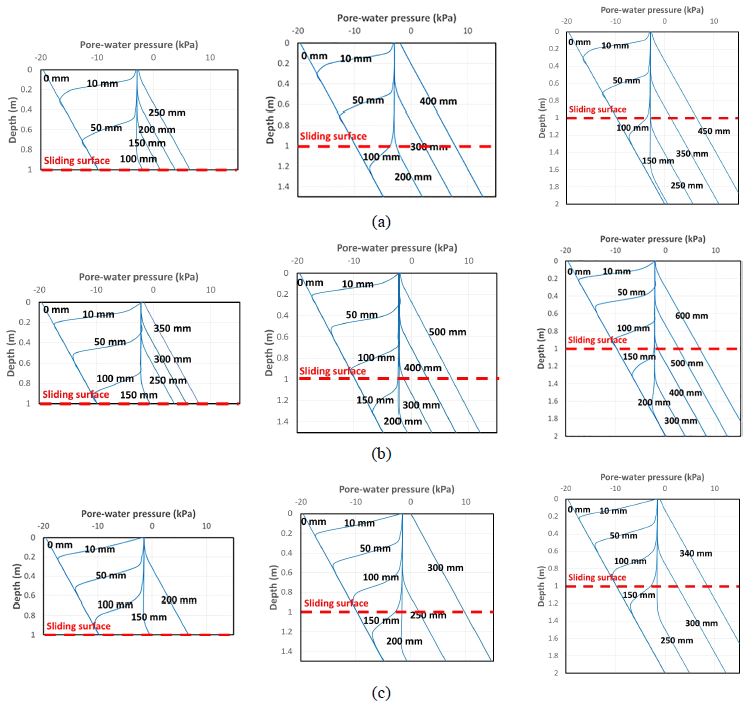
그림 7a는 서울 구룡산 일대 침투해석결과를 나타낸 것이다. 서울 구룡산 일대는 연구대상지역 가운데 흙-함수특성곡선 구배(m_w)가 중간정도 경사를 가지므로 토층내 침투 진행속도도 중간에 속한다. 토심 1 m 지역에서는 지반이 정수압 상태에 도달하기까지 250 mm 이상의 연속강우량이 침투되었고, 토심 1.5 m 및 2 m 지역에서는 각각 400 mm 이상과 450 mm 이상이 침투되었다. 그림 7b는 용인 멱조산 일대 침투해석결과를 나타낸 것이다. 용인 멱조산 일대 함수특성곡선의 구배는 연구대상지역 가운데 가장 가파르므로 토층내 침투과정이 가장 느리게 진행되었다. 토심 1 m 지역에서는 지반이 정수압 상태에 도달하기까지 350 mm 이상의 연속강우량이 침투되었고, 토심 1.5 m 및 2 m 지역에서는 각각 500 mm 이상과 600 mm 이상이 침투되었다. 그림 7c는 삼척 갈남리 유역 침투해석결과를 나타낸 것이다. 삼척 갈남리 일대 흙-함수특성곡선은 연구대상지역 가운데 구배(m_w)가 가장 완만하므로 토층내 침투과정이 가장 빠르게 진행되었다. 토심 1 m 지역에서는 지반이 정수압 상태에 도달하기까지 200 mm 이상의 연속강우량이 침투되었고, 토심 1.5 m 및 2 m 지역에서는 각각 300 mm 이상과 340 mm 이상이 침투되었다.

Fig. 7.

Continuous rainfall infiltration analyses at 1-m, 1.5-m, and 2-m soil-depth areas in (a) Mt. Guryong, (b) Mt. Myeogjo, and (c) Gallam basin.

4.1.3 결과 산출 및 연속강우 시나리오 선정

연속강우 침투해석 결과를 바탕으로, 그림 8은 연구대상지역 내 일부 특정 토심지역들에 대해 연속강우량에 따른 잠재적 전단활동면(potential sliding surface)에서의 간극수압 및 흡입응력과 사면경사에 따른 무한사면의 안전율 변화를 예시로 보여주고 있다. 본 연구에서는 Kim and Song (2015)의 국내 자연사면 산사태에 대한 방대한 현장조사 결과를 통해 가장 대표적인 전단활동면 깊이로서 1.0 m를 동일하게 가정하여 적용하였다. 서울 구룡산 일대의 경우 토심 2-m 지역(그림 8a)에서 연속강우량이 약 80 - 100 mm일 때 침윤전선이 잠재적 전단활동면 깊이에 도달하여 간극수압이 급격히 증가한다. 그 이후 거의 변화가 없다가 지하수위가 기반암 깊이에서부터 상승하여 연속강우량 약 200 mm일 때 전단면 깊이에 근접하게 올라오면서 간극수압이 다시 증가하여 양의 간극수압 상태에 들어서게 된다. 최종적으로 연속강우량이 약 420 mm 침투하였을 때 지하수위는 지표에 도달하여 사면은 정수압 상태가 된다. 사면경사가 약 40° 이상인 경우는 강우가 내리지 않는 상태에서도 불안정한 지역으로 계산된다. 사면경사가 약 15 - 40° 범위에 있는 경우에는 임계연속강우량이 약 250 - 420 mm 사이로 계산되며, 사면경사가 약 15° 이하인 지역은 사면이 정수압 상태에 도달하여도 사면안전율이 1.0 이하로 내려가지 않으므로 무조건 안정한 지역으로 계산된다. 용인 멱조산 일대의 토심 1.5-m 지역(그림 8b)에서는 연속강우량이 약 100-150 mm일 때 침윤전선이 잠재적 전단활동면의 깊이(1 m)에 도달하여 간극수압이 급격히 증가한다. 그 이후 거의 변화가 없다가 지하수위가 기반암 깊이에서부터 상승하여 연속강우량 약 400 mm일 때 전단면의 깊이에 근접하게 올라오면서 간극수압이 다시 증가하여 양의 간극수압 상태로 들어서게 된다. 최종적으로 연속강우량이 약 620 mm일 경우 지하수위는 지표에 도달하여 사면은 정수압 상태가 된다. 사면경사가 약 20 - 40° 범위에 있는 경우에는 임계연속강우량이 약 400 - 620 mm 정도로 계산되며, 사면경사가 약 20° 이하인 경우에는 사면이 정수압 상태에 도달하여도 사면안전율이 1.0 이하로 내려가지 않으므로 무조건 안정한 지역으로 계산된다. 삼척 갈남리 유역의 토심 1-m 지역(그림 8c)에서는, 연속강우량이 약 100-140 mm일 때 침윤전선이 전단면 깊이(1 m)에 도달하여 간극수압이 급격히 증가한다. 이 경우 전단면 깊이와 기반암 깊이가 일치하므로 침윤전선이 전단면에 도달하는 즉시 지하수위도 형성되어 상승하게 된다. 최종적으로 연속강우량이 약 220 mm 침투하였을 때 지하수위는 지표에 도달하여 사면은 정수압 상태가 된다. 사면경사가 약 50° 이상인 경우는 강우가 내리지 않는 상태에서도 불안정한 지역으로 계산된다. 사면경사가 약 20 - 50° 범위에 있는 경우에는 임계연속강우량이 약 130 - 220 mm 사이로 계산되며, 사면경사가 약 20° 이하인 지역은 사면이 정수압 상태에 도달하여도 사면안전율이 1.0 이하로 내려가지 않으므로, 무조건 안정한 지역으로 계산된다.

Fig. 8.

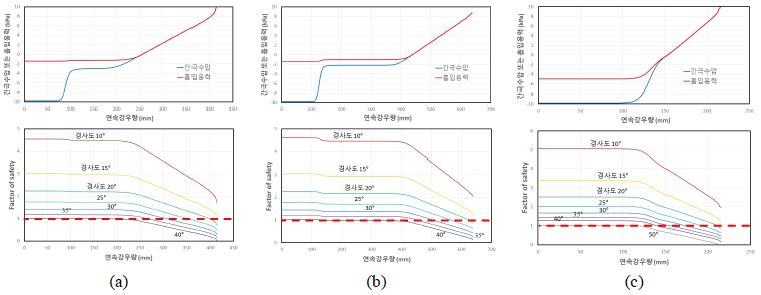
Variations of pore-water pressure, suction stress, and factor of safety at potential sliding surface with respect to continuous rainfall accumulations in (a) 2-m-soil-depth areas of Mt. Guryong, (b) 1.5-m-soil-depth areas of Mt. Myeogjo, and (c) 1-m-soil-depth areas of Gallam basin.

그림 9는 연구대상지역에 대해 최종적으로 도출된 임계연속강우량들의 분포를 나타낸 것이다. 서울 구룡산 일대의 경우(그림 9a), 토심 1-m 지역과 1.5-m 지역이 산지의 중상부에 많이 위치하고 있으며, 토심 1-m 지역의 임계연속강우량은 약 0 - 250 mm에 분포하고, 토심 1.5-m 지역의 임계연속강우량은 350 - 450 mm로 대부분 분포한다. 따라서, 서울 구룡산의 경우 연속강우량 150 mm, 250 mm, 350 mm 및 450 mm을 강우 시나리오로 선정하였다. 용인 멱조산 일대의 경우(그림 9b), 임계연속강우량 550 mm 근처에서 대부분의 셀이 분포하므로, 즉 연속강우량이 550 mm까지 누적되어야 산사태 위험지역이 크게 확장되는 것을 의미한다. 그러나, 현실에서 연속강우량이 550 mm까지 누적되는 경우는 매우 드문 비현실적인 값에 가깝다. 즉, 강우가 24시간 이상의 끊김 없이 최대 2일 정도 이내에 550 mm까지 누적되는 경우는 현실적으로 거의 관측된 바가 없다. 게다가, 임계연속강우량이 450 mm 이상인 지역은 대부분이 토심 2-m 지역이며 이 지역은 대부분 산지 하부의 완만한 지형이므로 산사태 발생시점부가 될 위험이 매우 낮은 지역으로 고려할 수 있다. 따라서 용인 멱조산 일대의 산사태 발생가능 시나리오는 연속강우량 450 mm 이하로 선정하고, 100 mm 간격으로 4개의 연속강우량(150 mm, 250 mm, 350 mm, 450 mm)을 강우 시나리오로 선정하였다. 삼척 갈남리 일대의 경우(그림 9c) 경사가 가파른 지형으로 인해 연속강우량이 0 mm인 경우에도 사면이 불안정한 지역이 존재하는 것으로 나타났다. 사질토 지반의 미약한 점착력을 고려하고 보수적인 설계를 위하여, 사면안정해석 시 점착력 항을 0으로 입력하였으므로 강우가 내리지 않는 시점에도 사면이 불안정 상태로 산출되는 지역이 있을 수 있다. 그 이상의 임계연속강우량은 100 mm 이상에서 나타나기 시작하였다. 최종적으로 50 mm 간격으로 총 5개의 연속강우량(100 mm, 150 mm, 200 mm, 250 mm, 300 mm)을 강우시나리오로 선정하였다.

Fig. 9.

Distributions of critical amounts of continuous rainfall and selections of continuous rainfall scenarios at (a) Mt. Guryong, (b) Mt. Myeogjo, and (c) Gallam basin.

4.2 연속강우 시나리오 기반 산사태 위험지도 작성

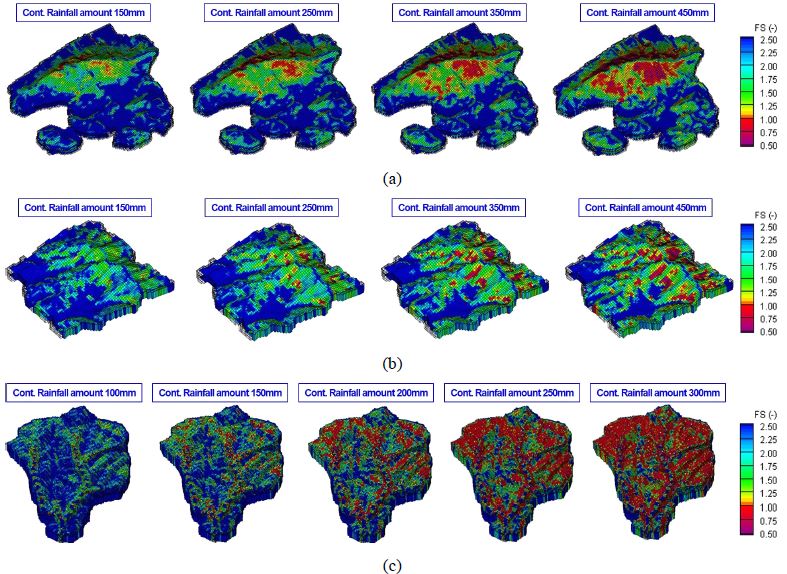
그림 10은 앞서 선정된 연구대상지역별 연속강우 시나리오에 따른 산사태 위험지도를 작성한 결과이다. 그림 10a는 서울 구룡산 일대에 선정된 4개 연속강우량(150 mm, 250 mm, 350 mm, 450 mm) 시나리오들을 물리기반 예측모형에 경계조건으로 적용하여 산사태 위험지도를 작성한 결과이다. 누적되는 연속강우량이 증가됨에 따라 사면안전율이 1.0이하인 산사태 위험지역의 범위가 확장되고 있음을 알 수 있다. 연속강우량이 150 mm일 경우 산사태 발생 위험구간은 정상부 부근 일부를 제외하고는 거의 없는 것으로 나타났으나, 그 이후 연속강우량이 커질수록 산사태 위험지역도 증가 및 확장됨을 알 수 있다. 그러나 경사가 완만하고 토심 1.5 m 이상인 산지 중하부 지역에서는 연속강우량이 450 mm가 되어도 산사태 위험지역이 적음을 확인할 수 있다. 그림 10b는 용인 멱조산 일대에 선정된 4개 연속강우량(150 mm, 250 mm, 350 mm, 450 mm) 시나리오들을 물리기반의 예측모형에 적용하여 산사태 위험지도를 작성한 결과이다. 서울 구룡산 일대와 마찬가지로 연속강우량이 증가됨에 따라 산사태 위험지역의 구간이 확장되고 있으나, 연속강우량이 450 mm가 되어도 서울 구룡산 일대에 비해 비교적 안정적인 지역이 더 많은 것을 확인할 수 있다. 지난 10년 이상의 기간 동안 멱조산 일대에서 산사태 피해가 보고되지 않았음을 고려했을 때 높은 강우량에도 비교적 안정적으로 도출된 본 산사태 위험지도는 타당한 결과로 판단할 수 있다. 그림 10c는 삼척 갈남리 유역에 선정된 5개 연속강우량(100 mm, 150 mm, 200 mm, 250 mm, 300 mm) 시나리오들을 물리기반의 예측모형에 적용하여 산사태 위험지도를 작성한 결과이다. 연속강우량이 증가됨에 따라 산사태 위험지역(사면안전율 1.0 이하인 빨간색 지역)의 범위가 급격하게 확장되고 있음을 알 수 있다. 해당지역의 경우 사면의 경사가 가파른 지형이 많으므로 연속강우량이 커질수록 산사태 발생 위험지역이 급격하게 증가하는 것을 확인할 수 있다. 또한 연속강우량이 300 mm에 도달하였을 때 산사태 발생 위험지역이 지배적으로 분포함을 확인할 수 있다. 삼척 갈남리 일대가 연구대상지역 가운데 가장 적은 연속강우량에도 가장 넓은 위험구간이 분포하는 것은 경사가 가파른 지형의 영향도 있지만 대상지역의 지반에 대한 불포화 특성으로 인해 침투가 빨리 진행된 영향도 큰 것으로 판단된다.

Fig. 10.

Landslide hazard maps according to continuous rainfall amounts at (a) Mt. Guryong, (b) Mt. Myeogjo, and (c) Gallam basin.

4.3 연구결과의 활용성 및 한계점

작성된 산사태 위험지도와 연속강우량에 대한 예보자료를 연동하는 경우 실시간으로 산사태 위험성에 대한 예측 판단이 가능하다. 즉 구룡산(그림 10a)을 예시로 들었을 때, 예보된 연속강우량이 0 - 150 mm 사이인 경우 “연속강우량 150 mm 산사태 위험지도”를, 150 - 250 mm 사이인 경우에는 “연속강우량 250 mm 산사태 위험지도”를, 250 - 350 mm 사이인 경우에는 “연속강우량 350 mm 산사태 위험지도”를, 350 mm 초과인 경우에는 “연속강우량 450 mm 산사태 위험지도”를 각각 보수적인 위험성 예측지표로 활용이 가능하다.

작성된 산사태 위험지도의 활용성을 고찰하기 위해, 그림 11과 같이 구룡산 일대와 갈남리 유역에서 산사태 발생 당시의 각 연구대상지역의 인근 강우 관측기록 자료를 수집하여 분석하였다. 2010년 구룡산 산사태가 발생한 날짜인 9월 21일에는 오후 1시경부터 본격적인 강우가 시작되어 오후 4시 경에는 연속강우량이 150 mm를 초과하였으며, 산사태 발생이 보고된 오후 6시 경에는 약 250 mm를 초과한 것으로 확인되었다(그림 11a). 구룡산을 대상으로 작성된 산사태위험지도에서도, 첫 번째(연속강우량 150 mm) 지도까지는 안정지역이 지배적이나, 연속강우량 250 mm인 두 번째 지도부터 산사태 위험지역이 급격히 증가한 것을 확인할 수 있다(그림 10a). 따라서, 연속강우량 150 mm가 초과되는 시점인 오후 4시 경부터 산사태가 발생한 오후 6시 경까지 “연속강우량 250 mm 산사태위험지도”를 활용하는 것은 보수적인 예측판단 측면에서 타당한 활용방식임을 도출할 수 있다. 한편, 동일 시간대에 멱조산은 최종 연속강우량이 150 mm를 약간 초과하였으며, 동일한 방식의 경우 해당 초과되는 시점에 산사태위험지도가 “150 mm 지도”에서 “250 mm 지도”로 변경된다(그림 10b). 그러나, 지도 상에서도 위험지역 증가가 크지 않은 것을 확인할 수 있듯이 해당지역에서는 산사태가 발생하지 않았다. 갈남리 유역에서는 연속강우량이 약 70 mm밖에 누적되지 않았으므로, 가장 안정한 첫 번째 위험지도인 “100 mm 지도”에서 다른 지도로 업데이트 되지 않으며(그림 10c), 실제로 산사태 또한 발생하지 않았다.

Fig. 11.

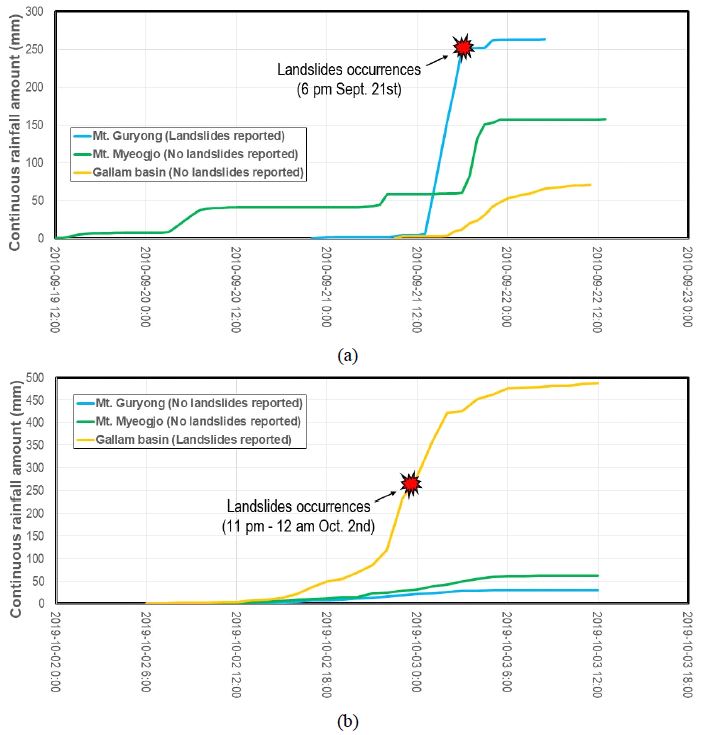
Continuous rainfall amounts recorded at three study areas around (a) September 21st in 2010 and (b) October 2nd in 2019.

갈남리 유역에서 산사태가 발생한 날인 2019년 10월 2일에는 오후 12시 경부터 강우가 시작되어 오후 9시-10시 사이에 연속강우량이 100 mm를, 오후 10시-11시 사이에는 200 mm를 각각 초과하였으며, 산사태 발생이 보고된 오후 11시-자정 사이에는 연속강우량이 250 mm를 초과한 것으로 확인되었다(그림 11b). 작성된 산사태 위험지도 상으로도, “연속강우량 250 mm 산사태위험지도”부터 산사태 위험지역이 우세해지는 것을 확인할 수 있으며 해당 지도의 활용 구간(연속강우량 200 - 250 mm)에서 산사태가 발생하였으므로 본 산사태위험지도의 보수적인 예측판단 지표로서의 적절성을 확인할 수 있다(그림 10c). 한편, 동일 시간대에 구룡산과 멱조산은 모두 연속강우량이 150 mm를 초과하지 않았으므로, 활용되는 지도는 가장 안정한 첫 번째 산사태 위험지도에서 다른 지도로 업데이트되지 않으며, 실제로 산사태 또한 발생하지 않았다.

본 연구에서 제안한 ‘연속강우량과 물리모형을 연계한’ 산사태위험지도 작성기법과 이를 활용한 산사태 위험지도 예측 활용성과 관련한 한계점에 대해 고찰하였다. 첫 번째로, 짧은 시간에 급격하게 연속강우량이 증가할 때 실시간 강우 관측자료를 활용하는 경우 산사태 대응 및 대피시간이 부족할 수 있다. 따라서, 산사태 재해의 선제적 관리에 활용하기 위해서는 연속강우량에 대한 예보자료를 연동하는 것이 필수적이라고 판단된다. 두 번째로, 제안된 방법을 통한 산사태 예측기술 수준이 ‘시점’을 판단하는 측면에서는 우수한 성능을 보였으나, 공간적으로 정밀한(pinpoint) 예측성능을 갖추기 위해서는 대상지역에 대한 지반 입력인자의 공간적 다양성 및 불확실성을 고려하여 정밀한 데이터베이스를 구축할 수 있는 방안이 필요한 것으로 판단된다. 세 번째로, 강우누적과 지반포화도 증가의 대응성이 보장될 수 있는 최대(한계) 강우지속시간을 설정할 수 있는 후속연구가 필요하다고 판단된다. 비록 최근의 연속강우 특성들은 대부분이 짧게는 수 시간 길게는 약 이틀 내에 지속이 종료되고 있으며 제안된 임계 연속강우량은 해당 지속시간 내에서 유효하나, 이보다 더 긴 지속시간에 걸쳐 점진적으로 강우가 누적되는 경우에는 산사태위험성을 과대평가하게 되는 경향이 증가한다. 네 번째로, 물리모형에서 강우 침투해석에 주요한 영향을 주는 토심과 초기조건을 광역지역에 대해서도 정밀하고 정확하게 현장을 반영할 수 있는 연구 및 기술이 필요하다고 판단된다. 이를 위해서는 장기적인 계획을 수립하여 지속적인 현장자료 수집과 지반 수리조건의 모니터링 활동이 필요하다. 이를 통해, 장기간 데이터 학습에 기반한 국내 자연사면 현장의 토심 및 초기조건에 대한 지능화 기술을 구축할 수 있을 것이라 생각된다.

5. 결 론

본 연구에서는 강우침투해석으로 산출된 지역 고유의 임계연속강우량들을 바탕으로 선정된 연속강우시나리오들을 산사태 물리모형에 연계함으로써 산사태 위험지도를 작성하는 방법론을 제시하고, 산출결과들의 타당성 및 활용성을 평가하였다. 이를 위해, 서울시 구룡산, 용인시 멱조산, 삼척시 갈남리 유역을 대상으로 지형, 토심, 각종 지반수리역학 입력인자들의 자료를 구축하였으며, 각 지역의 연평균 유효 강우강도를 적용하여 초기조건을 설정하였다. 서로 다른 불포화 특성을 가진 세 개 대상지역의 침투해석 결과 및 산사태위험지도 산출결과의 비교를 통해, 흙-함수특성곡선의 구배가 완만할수록 흙의 강우침투능이 좋으며, 이는 지형의 사면경사 조건과 함께 산사태 취약성(적은 연속강우량에서도 사면이 불안정해지는 경향)을 심화시키는 가장 결정적인 요인인 것으로 도출되었다.

물리모형에 연속강우량을 적용한 부정류 침투해석을 통해 산사태 위험지도를 각 지역에 대해 구축하였다. 전체적으로, 갈남리 유역, 구룡산, 멱조산 순으로 적은 연속강우량에도 산사태 위험지역이 많아지는 것으로 확인되었다. 특히 갈남리 유역 및 구룡산 일대는 연속강우량 250 mm부터 산사태 위험지역이 급격히 증가하고 우세해지기 시작하였으며, 이는 실제 산사태 발생 당시 관측된 연속강우량과도 일치하는 것을 확인할 수 있었다. 각 지역의 임계연속강우량 분포를 기반으로 적절한 구간을 선정하여 작성된 산사태 위험지도들은 실제 산사태 유발 연속강우 사건들을 대상으로 활용성을 테스트한 결과, 산사태 위험성에 대한 보수적인 예측판단 지표로서 그 적절성을 확인할 수 있었다. 궁극적으로 물리모형을 산사태 재해 선제적 관리에 실용화에 성공하기 위해서는, 지반 입력인자의 공간적 다양성 및 불확실성을 고려한 데이터 추정기술, 장기 모니터링에 기반한 연속강우량의 최적정의, 광역지역 산지현장의 토심 및 초기조건을 정확하게 추정할 수 있는 지능화 기술들을 개발하는 것이 필요하다.

Acknowledgments

본 연구는 한국지질자원연구원 기본사업인 “자연사면 산사태유발 고유연속강우량 원심모형실험 검증 및 산출모델 개발(계정번호:22-3812)” 및 “실시간 도시지역 산사태 조기경보기술 및 지질환경 오염물질 위험관리기술 개발(계정번호: 22-3412-1)” 과제의 일환으로 수행되었습니다.

References

• Baum, R.L., Savage, W.Z. and Godt, J.W., 2008, TRIGRS-A Fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis. version 2.0 (No. 2008-1159), US Geological Survey. [https://doi.org/10.3133/ofr20081159]
• Caine, N., 1980, The rainfall intensity-duration control of shallow landslides and debris flows. Geografiska Annaler Series A, 62, 23-27. [https://doi.org/10.1080/04353676.1980.11879996]
• Choi, G., Kwon, W.T., Boo, K.O. and Cha, Y.M., 2008, Recent spatial and temporal changes in means and extreme events of temperature and precipitation across the Republic of Korea. Journal of the Korean Geographical Society, 43, 681-700 (in Korean with English abstract).
• Choi, K.S., Moon, J.Y., Kim, D.W., Byun, H.R. and Kripalani, R.H., 2010, The significant increase of summer rainfall occurring in Korea from 1998. Theoretical and Applied Climatology, 102, 275-286. [https://doi.org/10.1007/s00704-010-0256-0]
• Choi, Y., Kim, M.G., Kim, Y.J. and Park, C., 2011, Characteristics and changes of extreme precipitation events in the Republic of Korea, 1954~2010: their magnitude, frequency, and percent to total precipitation. Journal of Climate Research, 6, 45-58.
• Cho, S.E., 2009, Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics. Engineering Geology, 105, 32-43. [https://doi.org/10.1016/j.enggeo.2008.12.007]
• Cho, S.E. and Lee, S.R., 2002, Evaluation of surficial stability for homogeneous slopes considering rainfall characteristics. Journal of Geotechnical and Geoenvironmental Engineering, 128, 756-763. [https://doi.org/10.1061/(ASCE)1090-0241(2002)128:9(756)]
• GEO-SLOPE International Ltd., 2012, Seepage Modeling with SEEP/W. GEO-SLOPE International Ltd., Calgary, AB, Canada.
• Guzzetti, F., Peruccacci, S., Rossi, M. and Stark, C.P., 2008, The rainfall intensity-duration control of shallow landslides and debris flows: an update. Landslides, 5, 3-17. [https://doi.org/10.1007/s10346-007-0112-1]
• Jeong, S.S., Hong, M.H. and Kim, J.H., 2018, A wireless sensor network technique and its application in regional landslide monitoring. Journal of the Korean Geotechnical Society, 34, 19-32 (in Korean with English abstract).
• Jung, I.W., Bae, D.H. and Kim, G., 2011, Recent trends of mean and extreme precipitation in Korea. International Journal of climatology, 31, 359-370. [https://doi.org/10.1002/joc.2068]
• Kim, K.S., Jeong, S.W., Song, Y.S., Kim, M. and Park, J.Y., 2021. Four-year monitoring study of shallow landslide hazards based on hydrological measurements in a weathered granite soil slope in South Korea. Water, 13, 2330. [https://doi.org/10.3390/w13172330]
• Kim, K.S. and Song, Y.S., 2015, Geometrical and geotechnical characteristics of landslides in Korea for various geological conditions. Journal of Mountain Science, 12, 1267-1280. [https://doi.org/10.1007/s11629-014-3108-z]
• Kim, Y.T., Joo, Y.S., Lee, S.R. and Shin, H.S., 2010, A Study on Weighting Factors affecting Steep-slope Failure considering Rainfall Infiltration, Primary Research Report. National Institute for Disaster Prevention, 209p (in Korean).
• Landslide Damage Status, 2022, https://www.index.go.kr/potal/stts/idxMain/selectPoSttsIdxMainPrint.do?idx_cd=1311&board_cd=INDX_001, (December 1, 2022).
• Lee, K., Baek, H.J., Cho, C.H. and Kwon, W.T., 2011, The recent (2001-2010) changes on temperature and precipitation related to normals (1971-2000) in Korea. The Geographical Journal of Korea, 45, 237-248 (in Korean with English abstract).
• Lu, N. and Godt, J., 2008, Infinite-Slope Stability under Steady Unsaturated Seepage Conditions. Water Resources Research, 44, W11404. [https://doi.org/10.1029/2008WR006976]
• Lu, N. and Likos, W.J., 2006, Suction stress characteristic curve for unsaturated soil. Journal of geotechnical and geoenvironmental engineering, 132, 131-142. [https://doi.org/10.1061/(ASCE)1090-0241(2006)132:2(131)]
• Montrasio, L., 2000, Stability analysis of soil-slip. Risk Analysis II, C.A. Brebbia (ed), WIT press, 357-366.
• Montrasio, L., Valentino, R., Corina, A., Rossi, L. and Rudari, R., 2014, A prototype system for space-time assessment of rainfall-induced shallow landslides in Italy. Natural hazards, 74, 1263-1290. [https://doi.org/10.1007/s11069-014-1239-8]
• National Institute of Meteorological Research, 2012, Global Climate Change Report 2012, 100 p.
• Oh, S. and Lu, N., 2015, Slope stability analysis under unsaturated conditions: Case studies of rainfall-induced failure of cut slopes. Engineering Geology, 184, 96-103. [https://doi.org/10.1016/j.enggeo.2014.11.007]
• Park, H.S., Kim, B.S. and Park, S.W., 2017, A Simple Method for Estimating Wetting Path of Soil Water Characteristic Curve on Unsaturated Soils. Journal of the Korean Geotechnical Society, 33, 37-48 (in Korean with English abstract).
• Park, J.Y., Lee, S.R., Oh, S., Lee, J.H., Jeon, J.S., Song, Y.S. and Park, H.S., 2020, Critical continuous rainfall map for forecasting shallow landslide initiations in Busan, Korea. Water, 12, 2404. [https://doi.org/10.3390/w12092404]
• Rossi, G., Catani, F., Leoni, L., Segoni, S. and Tofani, V., 2013, HIRESSS: A physically based slope stability simulator for HPC applications. Natural Hazards and Earth System Sciences, 13, 151-166. [https://doi.org/10.5194/nhess-13-151-2013]
• Saulnier, G.M., Beven, K. and Obled, C., 1997, Including spatially variable effective soil depths in TOPMODEL. Journal of Hydrology, 202, 158-172. [https://doi.org/10.1016/S0022-1694(97)00059-0]
• Simoni, S., Zanotti, F., Bertoldi, G. and Rigon, R., 2008, Modelling the probability of occurrence of shallow landslides and channelized debris flows using GEOtop‐FS. Hydrological Processes: An International Journal, 22, 532-545. [https://doi.org/10.1002/hyp.6886]
• Song, Y.S., 2014, Suction stress in unsaturated sand at different relative densities. Engineeirng Geology, 176, 1-10. [https://doi.org/10.1016/j.enggeo.2014.04.002]
• van Beek, L.H., 2002, Assessment of the influence of changes in landuse and climate on landslide activity in a Mediterranean environment. Ph.D. thesis, University of Utrecht, Utrecht, 363 p.
• van Genuchten, M.T., 1980, A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44, 892-898. [https://doi.org/10.2136/sssaj1980.03615995004400050002x]
• Wu, W. and Sidle, R.C., 1995, A distributed slope stability model for steep forested basins. Water Resources Research, 31, 2097-2110. [https://doi.org/10.1029/95WR01136]
• Yoon, S., Chang, S. and Park, D., 2022, Investigation of soil-water characteristic curves for compacted bentonite considering dry density. Progress in Nuclear Energy, 151, 104318. [https://doi.org/10.1016/j.pnucene.2022.104318]
• Yoon, S., Kim, M.S., Kim, G.Y. and Lee, S.R., 2021, Contemplation of relative hydraulic conductivity for compacted bentonite in a high-level radioactive waste repository. Annals of Nuclear Energy, 161, 108439. [https://doi.org/10.1016/j.anucene.2021.108439]