군집 분석과 지하수위 모델을 이용한 인위적 하천수위 조절에 따른 지하수위 영향 정량적 평가

1. 서 론

전국적인 하천 정비 사업의 결과로 주요 하천과 지류에 많은 수의 보와 댐이 건설되었다. 이렇듯 하천의 수위를 제한적인 범위 내에서 인위적으로 제어할 수 있게 됨으로써 관개용수 등의 확보가 용이해진 반면, 보 하류의 수위가 낮아지고 수량이 줄어 들게 되어 하천의 녹조 현상 등과 같은 환경적 문제를 야기할 수도 있다(Ju et al., 2016). 따라서, 하천 유역의 경우 지하수의 수량과 수질에 영향을 미칠 수 있는 지표수와의 상호작용이 더욱 중요하고, 특히 본 연구 지역인 금강 유역 일대는 수막 재배와 같은 농업 기술의 발달로 연중 농업 활동에 대한 지하수 의존도가 높으므로, 지하수위 변화의 다양한 원인을 정량적으로 분석하여 이를 정책에 반영하는 것이 중요하다.

일반적으로 지하수위는 지하수 함양, 증발산, 조석, 대기압, 지진과 같은 자연적인 요인과 구조물에 의한 외력, 지하수 양수, 터널 굴착 등의 인공적인 요인에 의해 변화할 수 있다(Freeze and Cherry, 1979). 대부분의 농업 지역에서 강우에 의한 지하수 함양과 관개 용수 사용이 지하수위 변화의 주요 요인이 되지만, 하천과 인접한 지역의 경우, 하천 수위가 지하수위 변화의 결정적 요인이 되기도 한다.

지하수위의 다양한 변화 요인을 시계열 자료 분석을 통해 규명하거나 미래의 지하수 거동을 예측하고자 하는 시도는 여러 연구자들에 의해 수행된 바 있으며, 주로 관측 자료에 기반한 통계적 방법론이 주로 활용되었다. 그 중에서도 강우량이나 하천 수위 변화와 같은 입력 요인과의 교차상관관계나 과거 수위자료와의 자기상관관계를 이용한 지하수위 변화 예측을 시도한 경우와(Jeong et al., 2010; Park et al., 2010; Choi et al., 2018; Kim and Lee, 2018; Kim et al., 2018; Lee et al., 2018), 해안 지역 조석에 의한 지하수위의 주기적 변화를 파워 스펙트럼 분석 등의 방법으로 분석을 시도한 사례가 주를 이루었다(Lee et al., 2001, 2004). 보다 정밀한 통계적 예측을 위해서는 박스-젠킨스(Box and Jenkins, 1976)의 방법론에 의한 자기회귀 누적이동평균 모형(auto-regressive integrated moving average (ARIMA))과 같은 시계열 모형이 주로 이용되며, 국내에서는 국가 관측망 지하수위 자료와 제주도 및 강변 여과지 주변 지하수위 변화에 적용된 바 있다(Yi et al., 2004; Lee et al., 2009). 하지만 이러한 모형은 지질 특성이나 강우량, 하천수위 등 지하수위 이외의 자료는 고려하지 않고, 평균, 분산 등 주로 통계적인 특징들의 선형 결합만으로 구성되므로, 지하수위 변화의 원인이 되는 복합적인 요인들의 개별적인 영향은 분리하여 고려할 수 없다는 단점이 있다. 최근에는 지지벡터기계(support vector machine)와 인공 신경망(artificial neural network)과 같은 기계학습이나 딥러닝을 이용한 예측 방법도 다양하게 개발되고 있다(Yoon, P. et al., 2014; Yoon, H. et al., 2016). 이전의 통계적 시계열 모형과 비교할 때 이들 방법은 다양한 입력 자료와의 비선형적 상관관계도 고려할 수 있다는 장점이 있지만(Yoon et al., 2016), 지하수위 변화를 일으키는 물리적 현상을 직접적으로 고려하지 않았다는 점에서 전술한 통계적 모형과 유사하다고 할 수 있다.

본 연구에 사용한 지하수위 모델(groundwater-level model)의 방법론은 미국 지질 조사소(United States Geological Survey)에서 대량의 농업 용수 사용으로 인한 지역 내 지하수위 변화를 해석하기 위하여 제안된 방법으로, 지하수위 변화를 다중 요인에 의해서 일어나는 변화의 합으로 가정하고, 이를 설명하는 물리적 모형을 이용해 구한 지하수위를 실측 지하수위와 비교하여 모델 파라메터를 추정하는 일종의 역산모델이다(O’Reilly, 2004; Halford, 2006; Halford et al., 2016). 다중 요인에 의한 지하수위 변화를 예측한다는 점에서 인공 신경망 모델과 유사점이 있지만, 개별 인자에 대해 각각 다른 물리적 모형을 적용 한다는 차별점이 있다. 인공 신경망 모델의 경우 추정하는 파라메터들이 물리적으로 무의미한 다항식의 계수인 반면, 지하수위 모델에서는 그 자체로 지배방정식을 구성하는 물리량에 해당하므로 입력 자료와 결과인 지하수위와의 상호 작용 기작을 이해하는 데 유용하다. 또한 역산 과정에서 추정된 파라메터 값을 이용하면 지하수위 총 변화량 중에서 강우량, 하천수위, 양수량 등 각각의 요인이 미치는 영향을 개별적으로 정량화하는 것이 가능하다.

본 연구의 연구 지역인 금강 유역은 최근 단계적인 보 개방을 통한 하천수위 조절이 있었으며, 이와 동시에 인근 지하수에 대한 모니터링이 광범위하게 수행되고 있다. 본 연구에서는 먼저 군집 분석을 통해 연구 지역 내 다수 관정에서의 지하수위 변화 양상과 하천수위와의 상호 연관성을 파악한 후, 지하수위 모델을 이용해 하천수위 조절이나 양수와 같은 인위적 요인이 지하수위에 미치는 시공간적 영향을 파악하고자 하였다. 아울러 지역 내 지하수 변화가 어떠한 개별 요인에 의한 것인지를 다양한 시나리오를 통해 정량적으로 분석하고자 하였다.

2. 연구 지역의 수리지질학적 특성

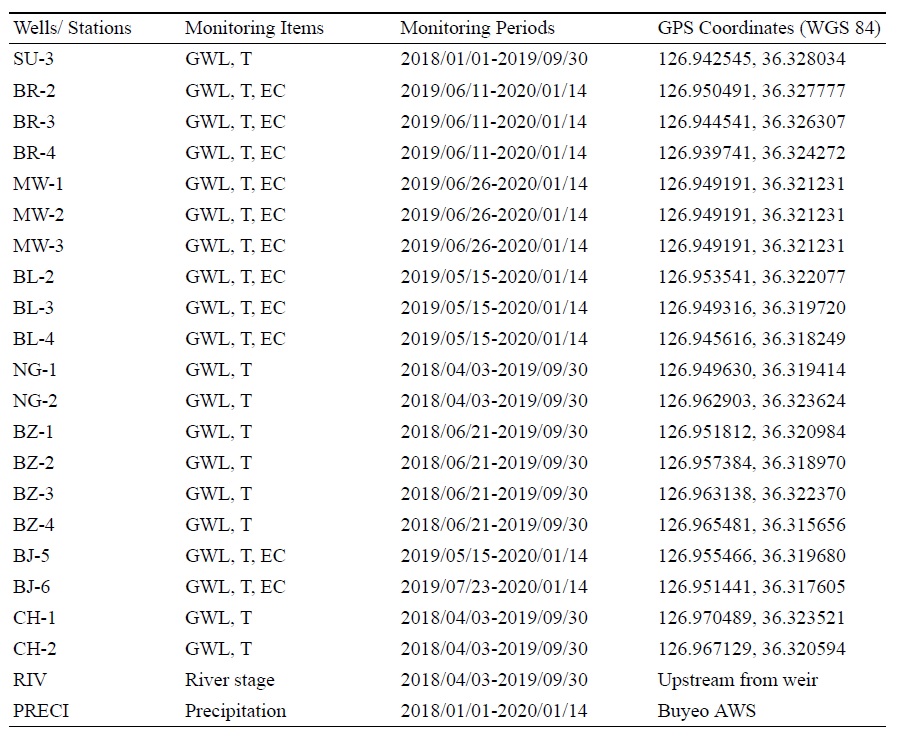
연구 지역은 공주와 논산 일대를 지나는 금강 유역(충청남도 부여군 부여읍 자왕리 일대)에 위치하고, 하류에 수위 조절이 가능한 보가 설치되어 있다(그림 1). 퇴적층은 하부 약 10 m 두께의 모래 자갈층과 상부 10 m 정도의 실트질 점토층으로 구성되어 있어, 피압 대수층의 형태를 보이고 있다. 수문 개방에 따른 지하수위 변화가 즉각적으로 나타나는 것으로 보아, 하부의 모래 자갈층은 하천과의 연결성이 우수한 것으로 생각된다. 지하수 이용은 주로 동절기 수막 재배와 하절기 시설 재배 시기에 집중된 것으로 조사된 바 있다(Korean Ministry of Environment, 2018). 하천 흐름 방향을 기준으로 우측 하안에 4개의 관측공(BR-2, 3, 4, SU-3)이 설치되어 있고, 좌안에는 16개의 관측정(MW-1, 2, 3, BL-2, 3, 4, NG-1, 2, BZ-1, 2, 3, 4, CH-1, 2, BJ-5, 6)이 설치되어 있다. 이중 MW-1, 2, 3은 동일 지점에 설치된 다심도 모니터링 관정으로 각각의 심도는 25 m, 15 m, 10 m 이다. 분석에 사용한 모니터링 관정의 위치와 측정 항목, 측정 기간은 하천수위, 강우량과 함께 표 1에 정리하였다.

Fig. 1.

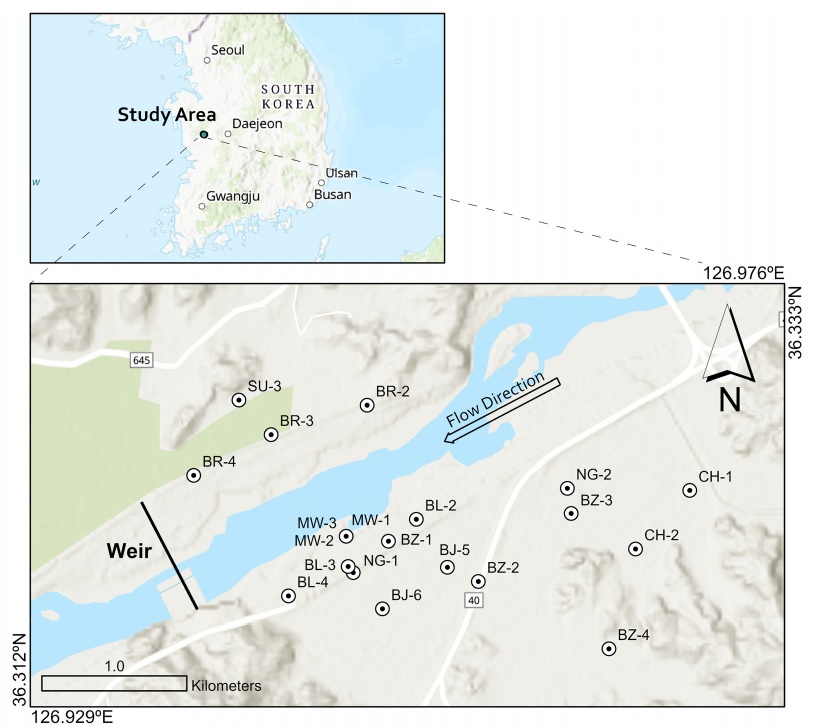
Regional and enlarged maps of the study area located in the riparian zone of the Geum River. The river stage can be artificially controlled by the weir constructed downstream of the river.

Table 1.

Lists of monitoring wells and stations, items, periods, and GPS coordinates used for the study (GWL: Groundwater Level, T: Temperature, EC: Electric Conductivity, AWS: Automatic Weather Station).

3. 연구방법

3.2 지하수위 모델

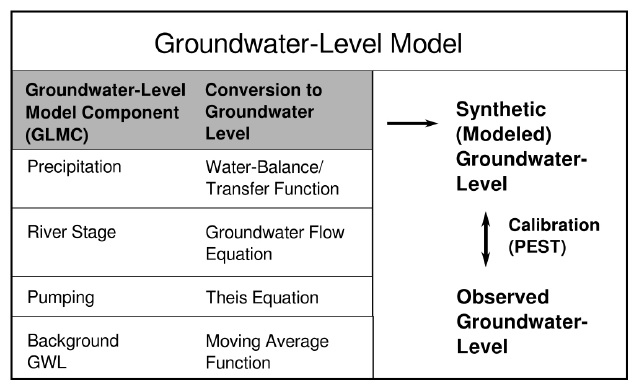
할포드 등(Halford et al., 2016)은 지하수위 모델을 이용해 실측 지하수위와 유사한 합성 지하수위(synthetic groundwater level; SGL)를 만들 수 있다고 가정하고, 합성 지하수위 변화에 기여하는 개별 요인을 지하수위 모델 요소(groundwater-level modeling component; GLMC)로 정의하였다. 일반적으로 기압 변화, 배경 지하수위 변화, 양수량 변화, 지구 조석(earth tides) 등을 지하수위 모델 요소에 포함할 수 있지만, 본 연구에서는 하천과 지하수의 상호 관계가 지하수위 변화의 주요 요인임을 감안하여 이를 추가로 고려하였다. 기압 변화는 실측 지하수위 자료에 이미 반영되어 있으므로 모델에서 제외하였고, 지구 조석에 의한 변화는 따로 고려하지 않았다.

개별 지하수위 모델 요소의 합으로 합성 지하수위의 계산이 가능하다면, 임의의 시간 t에서 합성 지하수위는 다음과 같이 나타낼 수 있다(Halford et al., 2016).

$$

(2)

위 식에서 SGL은 합성 지하수위이고, C₀는 실측 지하수위의 평균값과 합성 지하수위 평균값의 차이[L], n은 모델요소의 개수, GLMC_i는 i번째 모델 요소[L]이다. 지하수위 변화는 여러 원인이 복합적으로 작용하는 결과로 나타나므로, 개별 요인에 의한 변화 부분만을 알아내려면 먼저 해당 모델 요소를 이용해 지하수위 변화량으로 변환해야 한다. 예를 들어, 강우가 지하수위 상승에 미치는 영향을 파악하려면, 강우량 자료를 강우 모델 요소의 입력 자료로 하여 지하수위 상승 분으로 환산하는 방식이다. 이 변환 과정에서 물수지 이동함수(water-balance/transfer function model)가 사용된다(O’Reilly, 2004). 유사한 방법으로 하천수위 변화와 양수량이 지하수위에 미치는 영향도 해당 모델 요소를 사용하여 지하수위 변동 분으로 변환되고, 이 과정에는 지하수위 흐름 방정식과 타이즈 함수(Theis, 1935)가 사용된다.

지하수위 모델은 기존의 연속체 지하수 흐름 모델과 비교할 때, 보다 정밀한 보정을 통해 실측 자료에 매우 근접한 모델링이 가능한 장점이 있는 반면, 연속체 모델과 같이 지하수의 공간적인 유동 해석은 불가능하다는 단점이 있다.

그림 2는 지하수위 모델링의 과정을 나타낸 모식도이다. 본 연구에서는 강수량, 하천 수위, 양수량, 배경 지하수 변화를 지하수위 변동의 중요 요인으로 가정하였으므로, 먼저 각각에 해당하는 개별 모델 요소들로 지하수위 변화를 계산한 후, 합산하여 합성 지하수위 시계열을 만든다. 이렇게 생성된 합성 지하수위를 관측값과 비교하면서 각각의 모델 요소 방정식에 포함된 파라메터를 최적화하면 실제 지하수위 변동과 가장 유사한 모델을 만들 수 있다. 이 중에서 배경 지하수위 변동은 앞의 세가지 요인으로 설명되지 않는 지하수위의 단기적 또는 장기적 영향을 고려하기 위해 포함하였으며, 각각 다른 평균 기간을 가지는 3개의 이동 평균식으로 변환하여 모델에 반영하였다. 마지막으로, 파라메터 추정에는 지하수 분야에 널리 쓰이는 페스트(PEST) (Doherty, 2010)를 이용하였다. 페스트는 실측 지하수위와 합성 지하수위의 차이(잔차)를 목적 함수(objective function)로 하여 최소값을 구하는 방식으로 모델 보정을 수행한다. 모델링에 사용한 개별 모델 요소들은 다음에 상술한 것과 같은 방법으로 계산할 수 있다.

Fig. 2.

The schematic diagram showing procedure of the groundwater-level model.

3.2.1 강우 모델 요소

강수에 의한 지하수위 변화를 계산하기 위해 물수지 이동함수 모델을 이용하여 강수량을 지하수위 상승 분으로 환산하였다. 물수지 이동함수 모델은 물수지 모델과 이동 함수를 순차적으로 적용한 것으로 앞부분인 물수지 모델(water-balance model)은 강수량을 지표면 아래로의 침투량(infiltration rate)으로 변환하는 역할을 한다(O’Reilly, 2004).

$$

(3)

식 3에서 S는 총 수분 저장량(식물 뿌리 등에 의해 저장되어 있는 수분의 총량) [L], P(t)는 강수량에서 지표 유출량(runoff)을 제외한 수량 [L/T], E(t)는 증발산량 [L/T], t는 단위 시간을 의미한다.

이 중에서 증발산량은 해그리브(Hargreaves) 공식(Hargreaves, 1994), 펜만-몬티스(Penman-Monteith) 방법(Droogers and Allen, 2002) 등으로 추정이 가능한데, 본 연구에서는 기준 증발산량(reference evapotranspiration)과 해그리브 공식을 사용하여 월별 증발산량을 계산하였다(식 (4)).

$$

(4)

위 식에서 ET₀은 기준(잠재) 증발산량, K_ET는 매개변수이다. RA는 증발산량과 등가 단위로 환산한 대기권 상부층 태양 복사열(extra-terrestrial radiation) [L/T]로 월별, 위도별로 상이하다. TC는 일평균 기온(TC = (T_max - T_min)/2), TD는 최대 기온차 (TD = T_max - T_min), α는 TD에 대한 계수이다. 국내 여러 지역에 대한 K_ET값과 α값은 국내 연구자들에 의하여 제안된 바 있으며, 여기서는 충청남도 부여군에 해당하는 KET = 0.00154와 한반도 내륙에 해당하는 α = 0.58을 사용하였다(Moon et al., 2013). 식4에서 추정한 값이 잠재 증발산량임을 감안하면 실제 증발산량과의 오차를 피할 수 없지만, 이 부분에 대한 보정은 모델 수행 과정에서 별도로 고려하지 않았다.

침투량 계산을 위해 식 3을 시간에 대하여 이산화(discretization)하면 아래와 같은 식을 얻는다.

$$

(5)

위 식에서 ∆t는 이산화된 시간 구간을, S^k는 현재 시간 구간의 총 수분 저장량, S^k−1는 이전 시간 구간의 총 수분 저장량을 나타낸다. P^k와 ET^k는 각각 현재 시간 구간의 강수량(지표 유출량 제외) 및 증발산량이다.

일반적으로 강우로 증가한 토양 내 수분은 식물 및 불포화대에 머무르다 최대 저장량을 초과하면 지하수면까지 투과(percolation)되어 함양이 발생하므로, 실제 유효 침투량(effective infiltration)은 다음과 같은 버킷 모델(bucket model)로 나타낼 수 있다(O’Reilly, 2004).

$$

(6)

위 식에서 $$ { I}_e^k$$는 현재 시간 구간에서의 유효 침투량 [L/T], S_max는 최대 수분 저장량(최대 버킷량) [L]이다. 물수지 모델에 의해 계산된 침투량은 이동함수 모델의 입력값으로 사용되며, 강수의 침투에 의한 지하수 함양은 아래와 같은 침투량과 선형 이동 함수의 적분식으로 나타낼 수 있다고 가정하였다.

$$

(7)

위 식에서 r(t)는 지하수 함양량 [L/T], t는 시간 [T], ϕ(τ)는 시간 지연 인자 τ [T]에 대한 선형 이동함수를 나타낸다.

식 (7)에 감마 변환(gamma transform)을 적용하면, 최종적으로 침투량에서 지하수위 변화량을 계산하는 강우 모델 요소의 계산식을 구할 수 있다(O’Reilly, 2004).

$$

(8)

위 식에서 a_p는 강우 모델 요소의 진폭 배율(amplitude multiplier) [1], I는 침투량 [L], ∆t는 침투 이벤트 이후 시간 [T], Γ(n)는 감마 함수로 정수 n에 대해 n − 1의 값을 가진다. k와 n은 각각 감마 함수에 대한 스케일 파라메터 [T]와 형태 파라메터 [1]이다.

3.2.2 하천수위 모델 요소

하천수위에 따른 지하수위의 변화는 지하수 흐름 방정식으로 구하였다. 지하수의 외부 유입이나 유출이 없고, 하천 유역의 대수층을 균질하다고 가정하면 경계조건(하천수위) 변화에 따른 지하수위의 변화는 아래의 식과 같이 투수량계수(T)와 저류계수(S)를 포함하는 지하수 흐름 방정식(이 경우에는 확산 방정식(diffusion equation))의 해로 나타낼 수 있다.

$$

(9)

식 9에서 a_r는 하천수위 모델 요소의 진폭 배율 [1], Δh_r는 하천수위 변화량 [L], S는 저류계수 [1], T는 투수량계수 [L²T^-1], erfc는 에러 함수의 보함수(complementary error function)이다. 하천과 대수층의 경계면에서 지하수위 변화량은 하천수위 변화량과 같다고 가정하고 Δh_r에 대입하면, 하천으로부터 수직 거리(d)만큼 떨어진 곳에서 시간에 따른 지하수위의 변화를 계산할 수 있다.

3.2.3 양수 모델 요소

양수에 의한 지하수위 하강은 타이즈 방정식을 이용하여 계산한다.

$$

(10)

위 식에서 a_t는 양수 모델 요소의 진폭 [1], Q는 양수량 [L³T⁻¹], W는 타이즈 함수의 해를 구하기 위한 적분 함수 , r은 양수정에서 관측정까지의 거리 [L], ∆t는 양수 이후 시간 변화[T]를 나타낸다. 연구 지역 내 여러 개의 관정이 존재할 경우 각각의 계산 결과를 중첩하여 사용할 수 있다.

본 연구에서는 자료 부족으로 인하여, 시간에 따른 정확한 양수량을 특정하여 모델에 포함시키기 어려웠음으로 일정 지역 범위에서 일어나는 양수량의 합을 모델링 대상 관정 인근의 1개 관정에서 일어나는 것으로 가정하였다. 최종적으로 합성 지하수위를 만드는데 기여하는 개별 모델 요소의 중요도는 진폭 배율을 추정하는 과정에서 정해지므로, 양수량의 절대적인 크기보다는 시간에 따른 상대적인 변화량이 지하수위 모델 결과에 중요한 영향을 미친다.

3.2.4 배경 지하수위 모델 요소

연구에 사용한 지하수위 모델에 포함된 강수량, 하천수위, 양수량 변화 이외의 현상에 의해 일어나는 변화는 배경지하수위 변화에 반영되는 것으로 가정하기 때문에, 배경 지하수위 자료는 강수, 하천수위, 양수와 같은 세가지 요인으로부터 영향이 최소인 곳에서 취득하는 것이 이상적이다. 본 연구에서는 군집분석 결과 하천 좌안 구릉지 부근에 위치한 BZ-4의 지하수위가 하천수위의 영향이 가장 적고, 다른 지하수 관정에서의 변화와도 구별되는 상대적으로 일정한 변화를 보였으므로 배경 지하수위 자료로 사용하였다. 배경 지하수위는 식 11과 같이 이동 평균을 구하여 합성지하수위에 합산한다.

$$

(11)

위 식에서 a_bi는 진폭 배율 [1], V_i(t)는 지하수위의 이동 평균값 [L]을 나타낸다. 평균기간에 따라 시계열이 반영하는 물리 현상이 다르므로, 배경 지하수 모델 요소는 이동 평균 산출 기간에 따라 여러 개를 사용할 수 있다. 일반적으로 지하수위 변화에는 여러가지 주파수가 혼재되어 있다. 주로 대기압 변화가 반영되는 것으로 반일간, 주간, 또는 계절에 따라 다른 강도와 주기로 나타나고, 관정 제원과 대수층 특성에 따라서도 상이하게 나타난다. 반일 주기 변화는 관정과 대수층 사이의 연결성이 불량하거나 공내 저장량(wellbore storage)이 클수록 적게 나타난다. 관정 구경이 크거나 스크린 구간이 짧으면 단파장의 수위 변화가 감소하고, 저류계수가 크고 투수도가 낮은 대수층일수록 수위 변화량이 감소하는 경향이 있다(Halford et al., 2016). 본 연구에는 다양한 주기의 영향을 고려하기 위하여 1일, 1주일, 1개월의 평균 기간을 가지는 3개의 배경지하수위 모델 요소를 추가하였다.

3.2.5 파라메터 추정 및 모델 보정

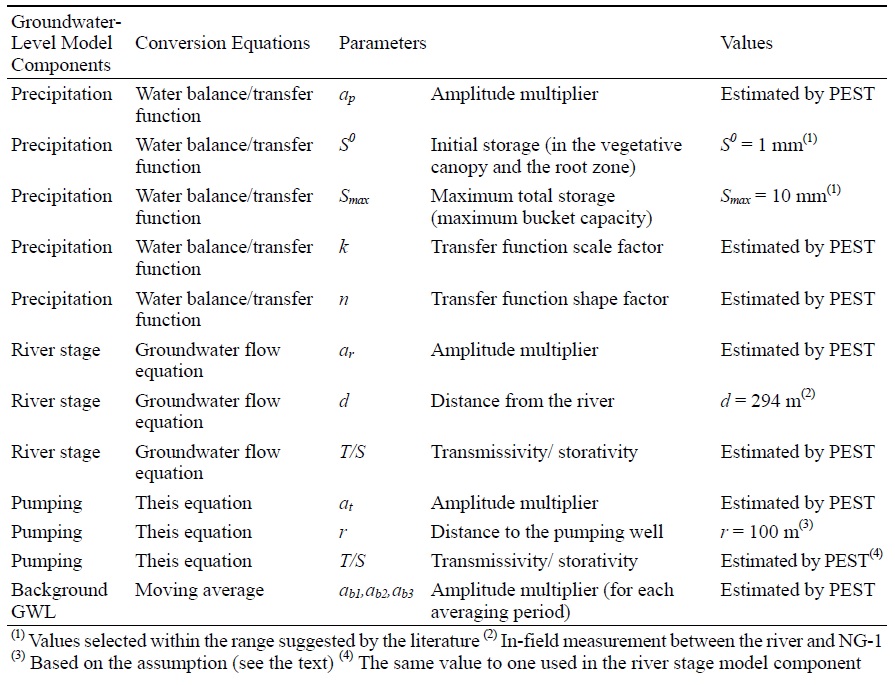
표 2는 합성 지하수위를 만드는데 사용한 개별 모델 요소에 사용된 파라메터와 그것의 추정 여부를 정리한 것이다. 각 모델 요소의 진폭 배율(a_p, a_r, a_t, a_bi)은 모두 추정한다. 강우 모델 요소의 경우 이동 함수의 형태를 결정하는 두개의 인자(k, n)를 추가적으로 추정한다. 이 인자들은 토양 내 불포화대의 성질을 반영하고, 이동 함수와 강우량 사이의 지연 시간 및 지하수위 피크의 강도와 폭에 영향을 미친다. 물수지 함수의 변수인 초기 수분 저장량(S⁰)과 최대 수분 저장량(S_max) 역시 토양의 성질과 관련이 있으며, 침투량 산정 시 사용된다. 여기서는 문헌에 있는 유사한 토질의 해당 값을 참고하여 각각 1 mm와 10 mm로 설정하였다(O’Reilly, 2004).

Table 2.

Groundwater-level model components with conversion equations and parameters, values used for the study.

하천수위 모델 요소에서는 투수량계수와 저류계수의 비율(T/S)을 추정하고, 하천과의 직선 거리(d)는 지도 상의 거리(NG-1의 경우 d = 294 m)를 사용하였다. 양수 모델 요소의 경우 하천수위 모델과 동일한 투수량계수/저류계수 비를 사용할 수 있다. 연구지역에서 양수는 비교적 넓은 범위에서 일어나고, 모든 농업용 관정에 대해 시간에 따른 양수량 변화 자료를 구할 수 없었으므로, 계산 상의 편의를 위해 관측정과 일정한 거리의 한 지점에서(r =100 m) 대부분의 양수가 일어나는 것으로 가정하였다. 배경 지하수는 각기 다른 3개의 평균 기간(1일, 1주일, 1개월)에 해당하는 이동 평균값을 구하여 세개의 모델 요소로 포함하고, 각각의 경우에 대하여 진폭 배율(a_b1, a_b2, a_b3)을 추정하였다.

지하수위 모델은 반드시 실측 자료와 비교하여 그 차이가 최소가 되도록 모델 요소의 파라메터를 보정하여야 한다. 이 과정을 효과적이고 정량적으로 수행하기 위하여 지하수 분야에서 널리 사용되는 파라메터 자동 추정 프로그램인 페스트(PEST)를 사용하였으며, 최소화를 위한 목적 함수 Φ는 다음과 같이 계산할 수 있다.

$$

(12)

위 식에서 X는 추정하는 파라메터들로 구성된 벡터, n은 비교 지점의 개수, SWL(X)_i은 합성 지하수위(모델링 결과), MWL(X)_i은 실측 지하수위를 나타낸다. 추정 결과의 효율은 식 (13)과 같은 제곱 평균 제곱근(root mean square) 값을 이용하여 나타낼 수 있다.

$$

(13)

파라메터 추정 과정에서 선택 파라메터 변환(selective parameter transformation)과 특이값 분해 정규화(singular-value decomposition regularization)를 적용하였다. 정규화 과정을 거치면 민감도가 낮거나 상관 관계가 높은 파라메터는 추정과정에서 제외되고 효과적인 추정이 가능해 진다(Doherty and Hunt, 2010).

4. 결과 및 토의

연구지역 지하수위 자료 군집 분석 결과 연구 지역의 지하수위는 변화 양상에 따라 크게 두 그룹(Group 1, 2)과 그 외 상관성이 약한 관정들로 나누어진다. 이 중에서 하천수위의 영향이 상대적으로 강한 관정들의 그룹인 그룹 1에 포함된 하나의 관정(NG-1)에 대해 지하수위 모델을 적용하고, 인위적인 하천수위 변화와 양수량 증가에 따른 지하수위 변화를 분석하였다.

4.1 하천수위가 지하수위에 미치는 영향

그림 3은 연구 지역 19개 관정(BJ-6 제외)의 지하수위와 하천수위(RIV로 표시)의 계층적 군집을 보여주는 계통도(dendrogram)로 세로축은 관정과 하천의 기호(괄호 안은 그룹 번호)를 나타내고, 가로축은 각 관정에서 계산한 피어슨 상관 관계 벡터 간의 거리를 나타낸다. 그림을 보면 지하수위 변화 양상에 따라 크게 두개의 그룹과 그외의 관정들로 구분되는 것을 확인할 수 있다. 그룹 1(청색 실선)은 그룹 내 구성원 간의 거리가 매우 가까운 것을 볼 때, 관정 간 상호 유사성 및 하천수위와의 유사성이 매우 높은 것을 알 수 있다. 그룹 2(적색 실선)도 관정 상호 간의 유사성은 높지만 그룹 1과는 구별되고, 하천수위와의 유사성도 그룹 1을 구성하는 관정 보다는 상대적으로 낮은 것으로 나타난다. 그 외 BZ-3, 4 및 BJ-5는 앞서 설명한 두 그룹에 속하지 않으며 다른 관정과 하천과의 유사성이 상대적으로 낮다. 특히 BZ-4의 경우는 다른 관정의 지하수위 자료와 매우 상이하게 나타나는데, 이는 지리적으로 하천 바깥쪽 구릉지에 위치하여 하천수위와 양수의 영향이 거의 반영되지 않기 때문이라고 생각된다.

Fig. 3.

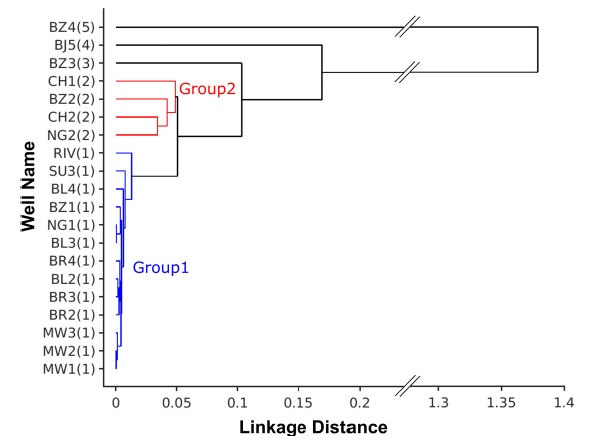
A dendrogram showing a hierarchical classification of wells and the river. X and Y-axes represent the linkage distance of Pearson’s correlation and well names, respectively (RIV: river stage level). Wells are classified into two groups by their groundwater change patterns. Wells linked with blue lines are referred to Group 1 and red as Group 2 in the text.

군집분석 결과를 그룹별로 지도상에 도시해 보면(그림 4), 그룹 1(청색 파선)은 주로 하천의 좌·우안에 위치하고 자연 제방과 상대적으로 가까운 곳에 위치한 반면, 그룹 2(적색 파선)는 하천 좌안의 자연 제방 안쪽에 위치하면서 그룹 1 보다는 상류에 위치한 관정이 많다. 또한 그룹 2는 하천과의 거리도 상대적으로 멀고, 안쪽의 낮은 구릉지(그림 1의 남동쪽 하단)와도 상대적으로 가까운 것으로 나타난다. 군집분석에서 다른 관정과 가장 상이한 지하수위 변화 양상을 보인 BZ-4의 경우는 하천과의 직선 거리가 가장 멀고 구릉지와 가까워 하천수위와 관개로 인한 영향이 거의 나타나지 않는다.

Fig. 4.

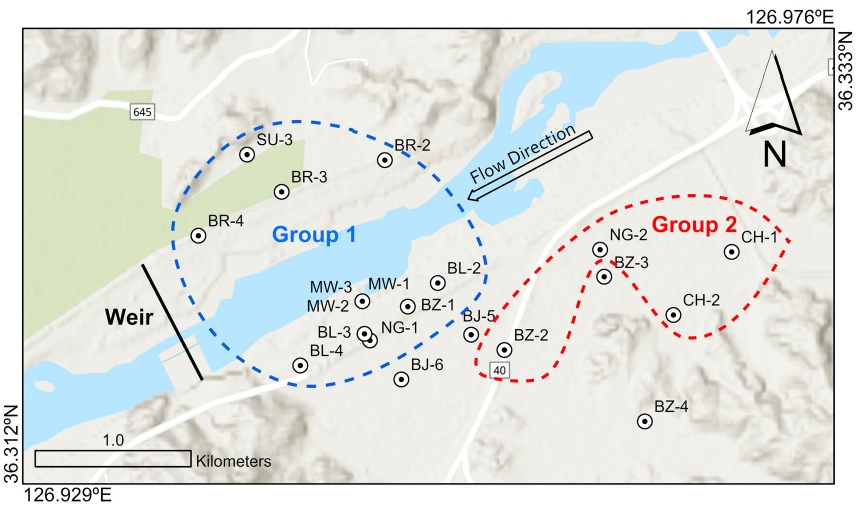
Spatial distribution of Groups 1 and 2 classified by the cluster analysis based on Pearson’s correlation ratio.

그룹별 지하수위 변화를 보면, 그룹 1은 하천수위 변화와 밀접한 상관관계를 보이고, 그룹 내 관정들 상호간 거동이 거의 일치하는 것으로 보인다(그림 5a). 2018년 7월과 9월에 강우량 증가로 인한 하천수위의 일시적 상승과, 하천 수위 1차 조절 기간인 2018년 9월과 11월 사이, 2차 조절 기간인 2019년 7월 이후의 하천수위의 단계적 하강이 지하수위 변화에 잘 반영되어 있다. 그룹2에 속한 관정들에서도 동일한 기간 중 하천수위의 영향이 나타나지만 그룹 1과 비교할 때 그 양상이 뚜렷하지 않다. 특히 1차 조절(2018년 9월 ~ 11월) 시에 나타난 하천수위의 하강은 그룹 1과 같이 하천수위 하강 단차에 비례하여 나타나지 않고, 오히려 2018년 8월 중순의 하천수위 하강이 상대적으로 크게 반영되어 있다(그림 5b). 마찬가지로 그룹 1은 2018년 7월과 9월 하천수위의 급격한 증가로 인한 지하수위 변동이 1 m 내외로 나타나는 반면, 그룹 2는 2~3 m로 상대적으로 더 크게 나타난다. 이와 함께 그룹2 관정에서는 단기적인 지하수위 상승과 하강이 반복되어 관찰되는데, 이는 관개 용수 사용으로 인한 지하수 양수 때문인 것으로 보인다. 대체적으로 그룹 1과 비교하여 그룹 2에 하천수위 변화의 영향이 적은 것은 하천과의 거리가 멀고 양수로 인한 지하수위 변화가 중첩되어 나타나기 때문이다.

Fig. 5.

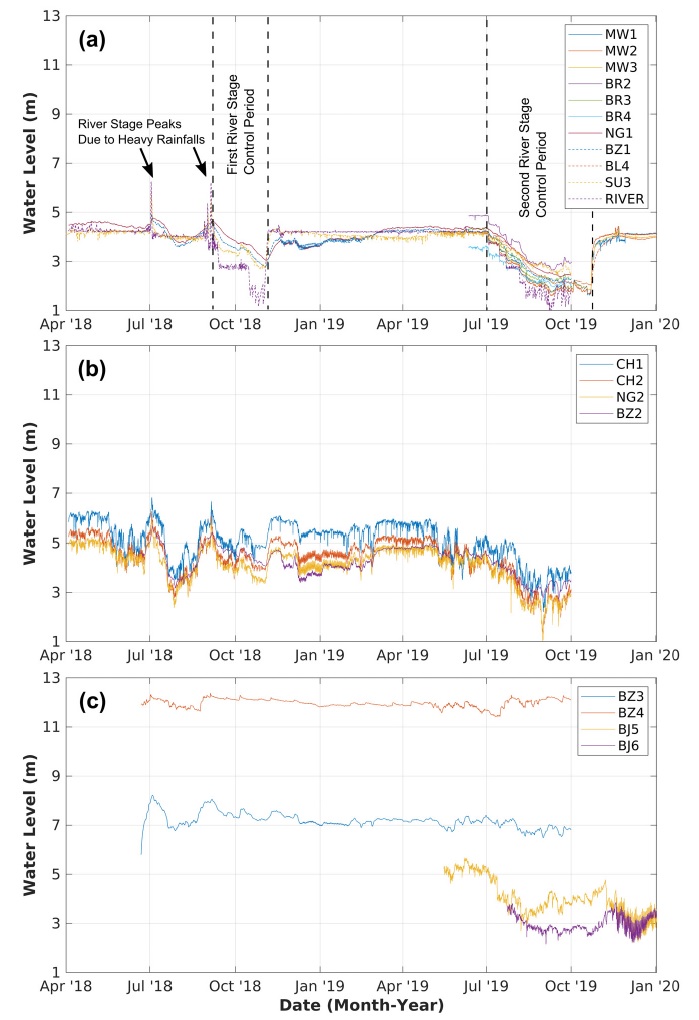
Groundwater level changes in Group 1, 2, and other wells not included in Groups 1 and 2. (a) Group 1 wells, (b) Group 2 wells, (c) Other wells.

두 그룹 이외의 관정 중에서는 하천과 구릉지의 중간 정도에 위치한 BJ-5와 BJ-6(군집분석에서는 제외)의 지하수위 변화 양상이 비슷하게 나타난다. 이들 관정은 지리적으로 그룹 1과 2의 중간 정도에 위치하는데, BJ-6는 2차 조절 기간의 전체적인 하천수위 하강을 잘 반영하지만 BJ-5의 경우는 하강하다 오히려 상승하고 있어 차이를 보여준다(그림 5c). BZ-3, 4 지하수위의 변화폭은 전체적으로 작고 비교적 일정하게 나타난다. BZ-3의 경우 2018월 7월과 9월 하천수위 급상승의 영향이 나타나는 것으로 보이지만, BZ-4의 경우는 BZ-3과 비교할 때 상대적으로 뚜렷이 나타나지 않고, 2차 조절 기간에도 하천수위 변화가 거의 반영되지 않는다. 이와 같은 현상이 나타나는 이유로, BZ-3, 4 두 곳은 구릉지 바로 아래 위치하고 하천과의 거리도 멀어서 주로 강우에 의한 변화 특성을 보기 때문으로 생각된다.

4.2 지하수위 모델 보정 및 요소별 기여도 추정

NG-1 관정은 하천과 가까운 곳에 위치하고 하절기와 동절기에 관개 용수의 수요가 많으므로, 이 지역에서 하천과 양수로 인한 지하수위 하강이 농업 활동을 어떠한 영향을 미치는지 판단하는데 유용하게 사용될 수 있다.

그림 6은 지하수위 모델링에 필요한 시계열 입력 자료이다. 각각의 모델 요소를 계산하기 위해서는 분석 기간 중 강우량과 하천수위, 양수량 및 배경 지하수위 변화 자료가 필요하다. 강우량 자료를 보면 대체로 7월 장마철과 9월에 시간당 20~30 mm의 많은 양의 비가 내리는 패턴이 반복되는데, 특히 2019년 9월에는 시간당 57 mm을 넘는 집중 강우가 내렸다(그림 6a). 강우량 자료는 3.2.1절에서 상술한 바와 같이 유효 침투량 계산을 거쳐 최종적으로 지하수위 변화 분으로 환산한다. 하천수위 변화(그림 6b)는 연구 지역 상류에서 측정한 값으로 연구 기간 중 2차에 걸친 수위 조절이 반영되어 있다. 1차 수위 조절(2018년 9월 ~ 11월)으로 하천수위는 2단계에 걸쳐 하강한 후 급격하게 회복하였고, 2차 조절에서는 하천수위를 5단계에 걸쳐 점진적으로 3 m 이상 하강하였다.

Fig. 6.

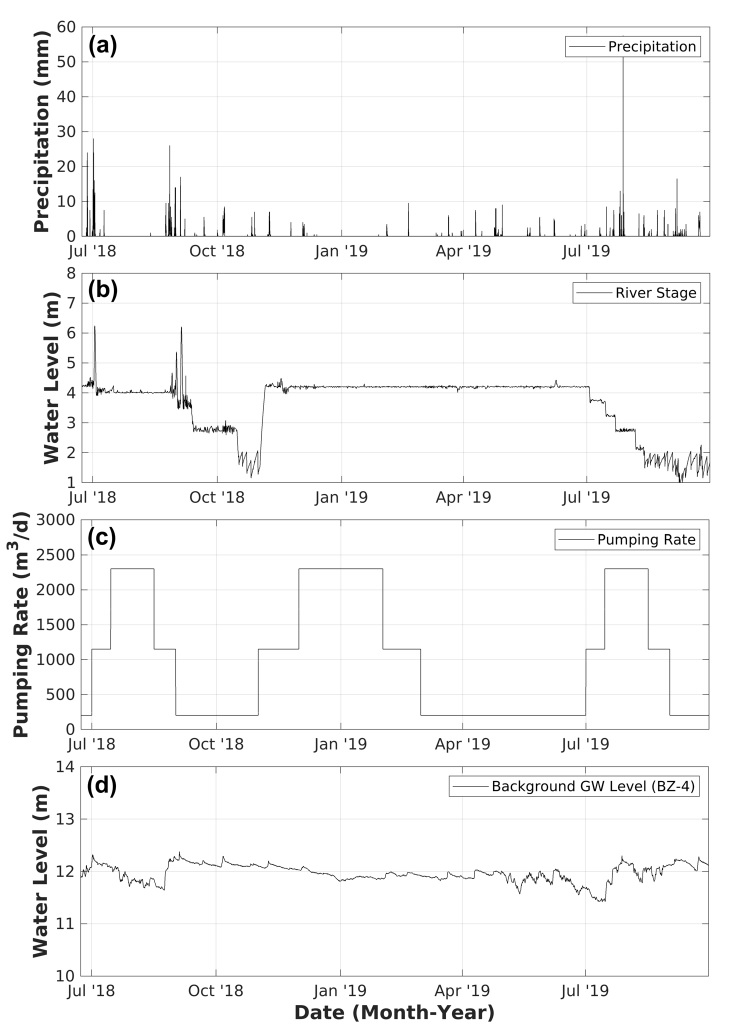
Input time series data for groundwater-level models. (a) Precipitation, (b) River stage level, (c) Pumping rate, and (d) Background groundwater level (BZ-4).

그림 6c은 현장 조사 추정치를 근거로 연구 지역의 연중 양수량 변화를 나타낸 그래프이다. 최근 조사에 의하면 양수량은 일년 중 기온이 가장 높은 7-8월과 수막 재배 기간인 11-2월 사이에 지역 내 집중되어 있으며, 조사 가능한 약 50개의 농업 용수 관정에서 측정한 평균 양수량은 관정당 5 ~ 46 m³/d 정도인 것으로 나타났다(KIGAM, 2019). 이와 같은 수치를 근거로 모델링 수행 시 연구 지역의 양수량을 연중 200 ~ 2,300 m³/d의 변화폭을 보이는 것으로 설정하고, 매년 동일한 양수 양상이 반복되는 것으로 가정하였다.

배경 지하수위 모델 요소 계산에는 BZ-4의 지하수위를 이용하였다(그림 6d). BZ-4는 군집분석 결과에서도 알 수 있듯이 연구 지역 지하수 관정 중에서 하천수위의 영향이 가장 약하고, 상대적으로 경작지와 먼 거리에 있어 하천과 양수, 두가지 요인에 의한 영향을 배제된 지하수위 변화를 보여 준다고 가정하였다.

NG-1의 실제 지하수위(실선)와 지하수위 모델 결과 생성된 합성 지하수위(파선)를 그림 7에 도시하였다. NG-1은 하천수위 조절 시마다 지하수위가 즉각적으로 하강하였는데, 1, 2차 조절 직전과 비교할 때 지하수위는 2 m가량 하강하였다. 모델 보정 과정은 특정 시점에서 합성 지하수위와 실측 지하수위가 가장 유사한 값을 가지도록 지하수위 모델 요소의 파라메터(표 2)를 최적화하는 방식으로 진행된다. 이 과정에서 보정 계산 시 시간 단축을 위하여 5일당 1개의 자료(십자 표시)에 대하여서만 목적 함수 계산을 수행하였다. 최종 보정 결과의 제곱 평균 제곱근 오차(root mean square error)는 0.15로 모델링 결과는 실측치와 전체적으로 잘 일치하는 양상을 보이며, 이는 추정한 각 모델 요소의 파라메터들이 연구 지역의 지하수계를 비교적 잘 반영하는 것을 의미한다. 그러나, 부분적으로 2018년 7월과 9월 집중 강우 사이의 모델값이 실측값에 비해 다소 과다하게 추정되었고, 두 차례 하천수위 하강 시에는 모델값이 실측값을 상당 기간 소폭 초과 또는 미달하는 구간이 나타나기도 한다. 또한 실측값의 시계열이 전체적으로 부드러운 곡선을 보이며 변화하는 반면, 모델값은 양수량과 하천수위 변화 시에 다소 급한 계단 형태의 변화를 보이기도 한다. 2018년 7월 ~ 9월 사이에 모델값이 과다 추정되는 원인으로, 이 기간 입력된 월평균 온도가 실제 연구 지역보다 측정 지점(부여 AWS)에서 다소 낮아 증발산량이 과소 추정되었거나, 모델링에 사용한 지하수 양수량이 실제보다 적을 가능성등을 생각할 수 있다. 최종적으로 최적화된 파라메터의 값은 표 3에 정리하였다.

Fig. 7.

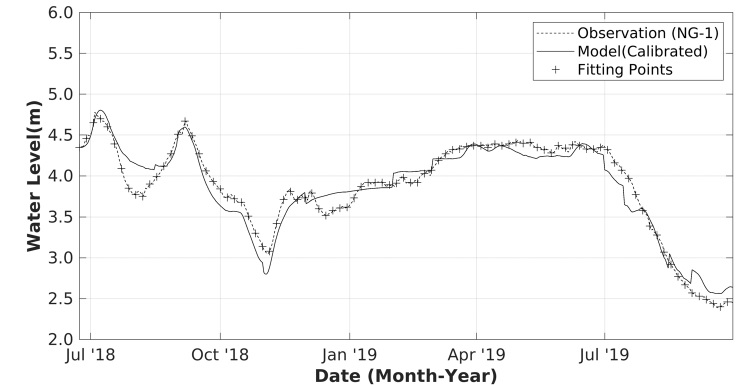
Observed and modeled groundwater levels for NG-1 after calibration. Only data at the fitting points (marked as crosses) are used for calibrating the model.

Table 3.

Groundwater-level model component parameters after best fit by PEST.

파라메터 추정 과정을 통해 지하수위 모델의 보정을 완료하면 모델 요소에 의한 지하수위 변화량을 개별적으로 구할 수 있으며, 이를 이용하면 각각의 요소가 지하수위 변화에 정량적으로 기여한 정도를 계산할 수 있다.

$$

(14)

MCC_i는 전체 지하수위 변화량에 대한 i번째 모델 요소의 기여도(model component contribution)를 나타내고 -1 ~ 1사이의 값을 가진다. 여기서 음의 값은 지하수위 하강에 기여한 정도를, 양의 값은 지하수위 상승에 기여한 정도를 나타낸다.

그림 8은 전체 분석 기간 중에서 각각의 모델 요소가 지하수 증가 및 하강에 기여한 정도를 적층식 막대 그래프(stacked bar chart)로 나타낸 그림이다. 2018년 7월 강우 시의 지하수위 변화를 보면, 수위 상승의 약 60% ~ 80%가 강우에 의한 것(청색)이고 일부는 하천수위 상승(적색)으로 인한 것임을 알 수 있다. 이 기간 중에도 양수에 의한 지하수위 하강 효과가 있지만(황색) 10% 미만으로 미미하다. 7월 이후에 이어지는 지하수위 하강은 이전 강우의 영향으로 상승한 지하수위의 회복, 하천수위 하강 및 양수에 의한 하강 등 복합적인 기여가 나타난 결과이다.

Fig. 8.

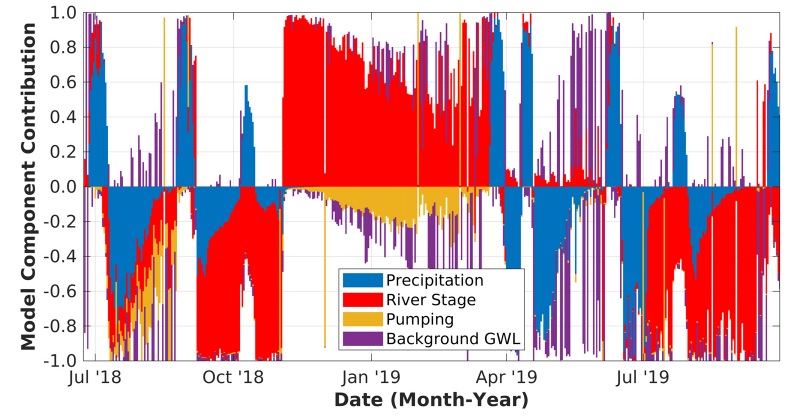
Model component contribution for groundwater level change plotted in a stacked bar chart. Positive values represent that model components contribute to raise the groundwater level, and negative to drop.

1차 수위 조절 기간(2018년 9월 ~ 11월)에 해당하는 기간에는 대부분 하천수위 하강과 강우에 의한 지하수위 변동 효과가 주로 나타난다. 시간에 따라 다르지만 이 기간 중에 하천수위 하강이 지하수위 하강에 기여하는 비율은 약 50% ~ 90%로 나타난다. 2018년 10월 중순에는 강우에 의한 양의 기여도와 하천 수위 하강에 의한 음의 기여도가 균형을 이루고 있어 지하수위 변동이 없는 구간이 나타나기도 한다.

2018년 11월 이후 하천 수위 복원으로 지하수위가 즉각적으로 회복하는데, 이 때의 지하수위 상승은 대부분 하천수위 상승에 기인한 것이다. 그 이후에 2018년 12월부터 수막 재배로 인한 양수에 의한 지하수위 하강 효과가 점진적으로 나타나고 하강에 대한 기여도는 최대 20% 정도로 나타난다. 하지만 이 기간 중에는 하천 수위 상승에 의한 효과가 크므로 지하수위는 대체로 상승하는 방향으로 나타난다(그림 5a).

2019년 3월 중순 이후에는 하천수위 변동과 양수량도 줄어들어, 이 시점부터 2차 수위 조절 기간이 시작하는 2019년 7월까지는 지하수위가 거의 변화가 없는 평형 상태를 유지한다. 이 구간에서는 인위적인 변동 요인이 대체로 제거되었으므로 지하수위는 소폭으로 상승과 하강을 반복하고 강우와 배경지하수위 같은 자연적인 요소가 지하수위 변화를 일으키는 주 요인이 된다.

2차 수위 조절 기간인 2019년 7월 이후에는 1차 수위 조절 기간과 비슷한 양상으로 하천 수위 하강과 강우에 의한 효과가 주로 나타난다. 특이할 만한 것은 이 기간 중에도 시설 재배로 인한 양수가 진행되었음에도 양수량 변화 시점을 제외하고는 기여도가 미미하게 나타난다는 것이다. 양수 시 수위 하강은 초기나 양수량 변화 시점에 주로 나타나고 일정 시간을 지나면 평형 상태에 도달하므로 대부분의 기간에 걸쳐 지속적으로 나타나는 하천 수위 하강에 비하면 상대적으로 기여도가 적게 나타나는 것으로 이해할 수 있다.

4.3 하천수위 조절과 양수가 지하수위에 미치는 영향

지하수위 모델을 이용하면 다양한 시나리오에서 하천수위 조절과 양수로 인한 지하수위 변화를 예측할 수 있다. 앞서 추정한 모델 요소들의 진폭 배율을 조절하여 지하수위 변화에의 기여도를 조절하거나 진폭을 0으로 설정하여 해당 모델 요소를 완전히 배제한 합성 지하수위를 생성하는 것이 가능한데, 이를 이용하면 지하수위 변화가 어떠한 요인에 의해 주로 결정되는 가를 여러 경우의 수를 통해 정량적으로 파악할 수 있다.

표 4는 하천수위 조절과 양수 중 1개 또는 2개 모델 요소를 포함하거나 제거한 시나리오이다. 모든 경우에 있어서 강우와 배경 지하수의 영향은 기본적으로 고려하였다.

Table 4.

Groundwater level modeling case scenarios.

Case 1은 강우, 배경 지하수와 함께 하천수위와 양수의 영향을 모두 고려할 때의 경우로 앞서 수행한 모델의 보정 결과와 동일하다. Case 2는 하천수위 하강에 의한 영향을 고려하고 양수에 의한 영향을 배제한 경우이다. 조사 지역에서 농업 활동에 의한 양수가 일어나지 않고 하천수위 하강에 의한 지하수위 변화만을 알 수 있으므로 두 가지 요인을 독립적으로 고려하기에 유용한 시나리오이다. Case 3은 반대로 양수에 의한 영향을 고려하고 하천수위의 영향을 배제한 것 이다. 이 경우는 조사 지역 내에서 하천수위의 조절이 일어나지는 않았지만 농업 관개는 계속되었을 때의 지하수위 변화를 보여준다. 마지막으로 Case 4에서는 비교를 위하여 하천수위와 양수에 의한 영향을 모두 배제하여 자연 상태에서 강우와 배경 지하수의 영향만을 반영한 지하수위를 모사하였다. 하천수위와 양수의 영향을 제거하려면 추정을 통해 얻은 다른 파라메터들을 유지한 채로, 해당 모델 요소의 진폭 배율을 0으로 설정하면 된다. 예를 들면, 양수량의 영향을 제거하기 위해 양수량 모델 요소의 진폭 배율(a_t)을 0으로 설정한다. 양수량 입력 자료를 모든 시간에 대해 초기값과 동일한 값으로 일정하게 하는 것도 진폭 배율을 조절하는 것과 동일한 결과를 만든다.

그림 9a는 실제 지하수위 관측값과 표 4의 시나리오를 통해 생성한 합성 지하수위를 비교한 그래프이다. Case 1(흑색 실선, + 표시)은 모든 모델 요소를 고려한 최후 보정 결과이므로 실측값(흑색 파선)과 가장 잘 일치한다. 여기서 자연적인 요소(강우와 배경 지하수)와 하천수위 변화만을 고려하면, 즉 양수에 의한 효과를 제거하면, Case 2(적색 실선, o 표시)을 얻는다. Case 2의 경우, 1, 2차 하천수위 조절에 의한 효과가 반영되어 지하수위가 하강하고 이 기간 중에 실제 관측된 지하수위 값과는 잘 일치한다. 하지만 양수에 의한 지하수위 하강의 영향은 고려되지 않았으므로 수막 재배로 인한 관개 용수 사용량이 증가하는 2018년 11월 ~ 2019년 3월과 2019년 7월 ~ 9월 사이에 실측값 보다 모델값이 상대적으로 높게 예측된다.

Fig. 9.

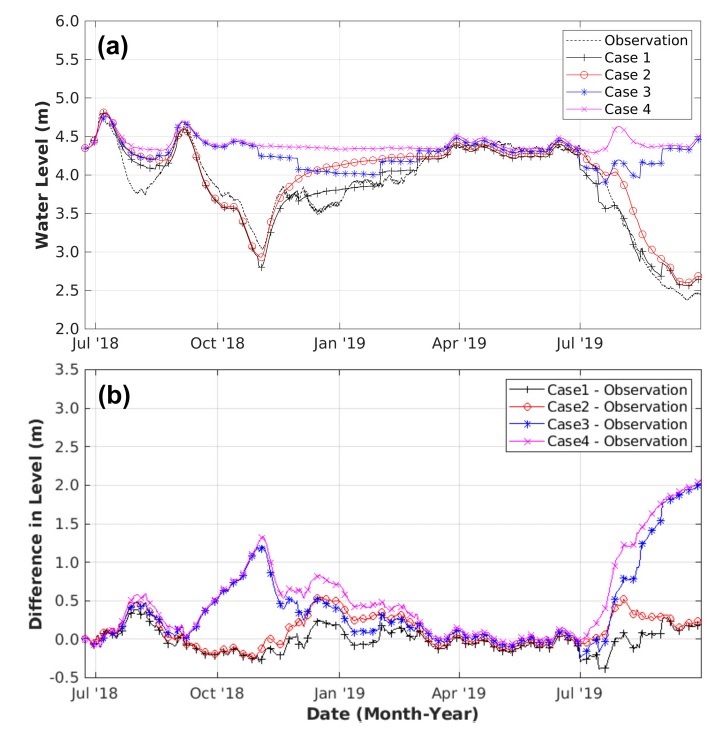
Groundwater-level modeling results by the case scenario listed in Table 4. (a) Observation and modeled groundwater level changes, (b) Difference in level between observation and modeled groundwater level changes.

반면, Case 3(청색 실선, * 표시)과 같이 하천수위의 변화가 없다고 가정한 상태에서 관개 용수 사용만을 고려하면 1, 2차 하천수위 조절의 영향을 전혀 받지 않고 조절 기간 중 지하수위가 거의 일정하게 유지되는 것을 확인할 수 있다. 그러나 양수에 의한 영향은 지하수위에 반영되므로, 역시 2018년 11월 ~ 2019년 3월과 2019년 7월 ~ 9월 기간 동안 관개로 인한 단계적 하강이 나타난다. Case 4(분홍색, x 표시)와 같이 인위적인 요소(하천수위 조절과 양수)를 모두 제거하면 지하수위는 규모가 강우 이벤트에 소폭 상승하는 것을 제외하고, 대체로 4-5 m 구간에서 거의 일정하게 유지되는 것을 확인할 수 있다.

그림 9b는 각각의 경우에 해당하는 모델 결과와 실측 지하수위와의 차이를 도시한 그래프이다. 그림과 같이 만약 조사 기간 내 하천수위 조절이 없었다면(Case 3, 4), 지하수위는 관측된 것 보다 1차 조절 시 에는 최대 1.3 m, 2차 조절 시에는 최대 2 m 가량 높을 것이라고 예측할 수 있다.

Case 1, 2와 실측 지하수위의 차이를 비교하면 하천수위 하강에 추가된 양수의 영향을 파악할 수 있는데, 주요 양수 기간인 2018년 11월 ~ 2019년 3월 사이에는 0.4 m 정도, 2019년 7월 ~ 9월 기간에는 최대 0.5 m정도 양수에 의한 추가적인 지하수위 하강이 일어난 것을 알 수 있다. 반면에 하천수위 조절과 관개 용수 사용이 상대적으로 적은 2019년 4월 ~ 7월까지는 지하수위 변화에 자연적인 요소가 지배적인 영향을 미치는 구간이므로 모델 결과와 실측값과의 차이가 거의 0에 가깝게 나타난다.

5. 결 론

본 연구에서는 하천과 인접한 농업 지역의 지하수위 실측 자료를 기반으로 인위적인 하천수위 조절과 농업용 지하수 사용이 지하수위에 미치는 영향을 군집 분석과 지하수위 모델을 이용하여 정량적인 해석을 시도하였다.

피어슨 상관계수를 사용하여 지하수위 변화 양상의 유사성에 따라 군집 분석을 실시한 결과, 연구 지역의 지하수위는 주로 하천과 구릉지 사이의 지리적인 위치에 크게 영향을 받는 것으로 나타났다. 하천수위 변화에 대한 민감도에 따라 크게 두 그룹과 그 외 관정들로 나누어지는데, 하천과 보에 상대적으로 가까운 좌우 하안 제방 근처에 위치한 관정에서 하천수위 변화의 영향이 가장 강하게 나타나고, 안쪽 구릉지에 근접할수록 하천에 의한 영향은 감소하고 강우와 지하수 함양에 의한 영향이 상대적으로 강하게 나타난다.

지하수위 모델을 이용하면 강우, 하천수위, 양수량 등과 같은 주요 요인들이 지하수위 변화에 미치는 기여도를 정량화하는 것이 가능하며, 이 경우 인위적 하천수위 하강이 지하수위 하강에 미치는 영향은 약 50%~90%인 것으로 나타났다. 이와 함께 다양한 모델링 시나리오를 비교한 결과, 인위적인 하천수위 조절이 하천과 연결성이 좋은 관정에서 약 1.5-2.0 m 정도의 지하수위 하강을 야기하였으며, 이 때 양수에 의한 추가적인 하강은 최대 0.5 m 정도인 것으로 나타났다.

앞으로 추가적인 연구를 통해 지하수위 모델링 기법을 연구 지역 전체 관정에 적용하면 하천수위 변화에 따른 지하수위의 공간적 변화 양상도 정량적으로 파악할 수 있을 것으로 기대된다. 향후 이러한 연구 결과는 하천 환경 보존과 농업 생산성 향상을 의한 최적의 하천 관리방안 수립에 활용될 수 있을 것이다.

Acknowledgments

이 연구는 2020년도 과학기술정보통신부에서 지원한 주요사업(기후변화 대응 대용량 지하수 확보 및 최적활용 기술 개발, 과제 번호: 20-3411)의 도움으로 수행되었습니다. 분석에 사용된 지하수위 자동관측 자료를 제공해 주신 한국수자원공사 관계자와 익명의 검토자 분들에게 감사드립니다.

References

• Box, G. and Jenkins, G.M., 1976, Time Series Analysis-Forecasting and Control. Holden-Day, San Francisco, California, USA, p. 575.
• Choi, M.R., Lee, H.J. and Kim, G.B., 2018, Characteristics of short term changes of groundwater level and stream flow rate during 2017 Pohang earthquakes. Journal of the Geological Society of Korea, 54, 557-566 (in Korean with English abstract). [https://doi.org/10.14770/jgsk.2018.54.5.557]
• Doherty, J., 2010, Methodologies and Software for PEST-Based Model Predictive Uncertainty Analysis. Watermark Numerical Computing.
• Doherty, J.E. and Hunt, R.J., 2010, Approaches to highly parameterized inversion - A guide to using PEST for groundwater-model calibration: Scientific Investigations Report 2010-5169. U.S. Geological Survey, p. 59. [https://doi.org/10.3133/sir20105169]
• Droogers, P. and Allen, R.G., 2002, Estimation reference evapotranspiration under inaccurate data conditions. Irrigation and Drainage Systems, 16, 33-45. [https://doi.org/10.1023/A:1015508322413]
• Freeze, A. and Cherry, J., 1979, Groundwater, 2th. Prentice-Hall, New Jersey, p. 604.
• Halford, K., 2006, Documentation of a Spreadsheet for Time-Series Analysis and Drawdown Estimation. Scientific Investigations Report 2006-5024, 1-38. [https://doi.org/10.3133/sir20065024]
• Halford, K., Garcia, C.A., Fenelon, J. and Mirus, B., 2016, Advanced Methods for Modeling Water-Levels and Estimating Drawdowns with SeriesSEE, an Excel Add-in: Techniques and Methods 4-F4. U.S. Geological Survey, p. 29 [https://doi.org/10.3133/tm4F4]
• Hargreaves, G.H., 1994, Defining and using reference evapotranspiration. Journal of Irrigation and Drainage Engineering, 129, 53-63.
• Jeong, J.M., Park, Y.C., Jo, Y.J. and Lee, J.Y., 2010, Time series analysis of groundwater level fluctuation data in Cheonjeonri, Chuncheon, Gangwon-do. Journal of the Geological Society of Korea, 46, 171-176 (in Korean with English abstract).
• Ju, H., Choi, I., Yoon, J., Lee, J., Lim, B. and Lee, S., 2016, Analysis of Cyanobacterial Growth Pattern in Bekjae weir During Recent 3 Years. Proceedings of Joint Meeting of Korean Society of Water and Waste Water and Korean Society on Water Environment, 562-563 (in Korean).
• Kim, E.J., 2016, Introduction to Artificial Intelligence, Machine Learning, and Deep Learning: Practice with Algorithm. 4th ed, Wikibooks, p. 338 (in Korean).
• Kim, G.B., Choi, M.R., Lee, C.J., Shin, S.H. and Kim, H.J., 2018, Characteristics of spatio-temporal distribution of groundwater levels change after 2016 Gyeong-ju earthquake. Journal of the Geological Society of Korea, 54, 93-105 (in Korean with English abstract). [https://doi.org/10.14770/jgsk.2018.54.1.93]
• Kim, I. and Lee, J., 2018, Influencing factor analysis on groundwater level fluctuation near river. Ecology and Resilient Infrastructure, 5, 72-81 (in Korean with English abstract).
• Kim, T.H., Moon, D.C., Park, W.B. and Ko, G.W., 2007, Classification of springs of Jeju Island using cluster analysis of annual fluctuations in discharge variables: investigation of the regional groundwater system. Geosciences Journal, 11, 1-17. [https://doi.org/10.1007/BF02857055]
• Korea Institute of Geoscience and Mineral Resources (KIGAM), 2019, Integrated Technology Development for Securing Groundwater/Geothermal Resources and Conserving Ecosystem according to Climate Change. Technical Report, p. 384 (in Korean with English abstract).
• Korean Ministry of Environment, 2018, Detailed Report for Effects of Weir Opening on Groundwater, p. 238 (in Korean).
• Lee, B.J., Koh, K.W., Moon, S.H., Park, Y.S. and Lim, M.T., 2004, Identification of Seawater Encroachment based on the Characteristics of Tidal fluctuation of Groundwater Level. Journal of the Geological Society of Korea, 40, 53-64 (in Korean with English abstract).
• Lee, B.J., Moon, S.H., Cho, B.W., Sung, I.H. and Lee, C.W., 2001, Identification of influences on groundwater fluctuations using spectrum analysis. Journal of the Geological Society of Korea, 37, 287-296 (in Korean with English abstract).
• Lee, H.A., Hamm, S.Y. and Nam, C.W., 2018, The abnormal groundwater changes as potential precursors of 2016 ML 5.8 Gyeongju earthquake in Korea. Economic and Environmental Geology, 51, 393-400
• Lee, S.I., Lee, S.K. and Hamm, S.Y., 2009, A Model for Groundwater Time series from the Well Field of Riverbank Filtration. Journal of Korea Water Resources Association 42, 673-680 [https://doi.org/10.3741/JKWRA.2009.42.8.673]
• Moon, J.W., Jung, C.G. and Lee, D.R., 2013, Parameter regionalization of Hargreaves equation based on climatological characteristics in Korea. Journal of Korea Water Resources Association, 46, 933-946 (in Korean with English abstract). [https://doi.org/10.3741/JKWRA.2013.46.9.933]
• Mukaka, M.M., 2012, Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Medical Journal, 24, 69-71.
• O’Reilly, M., 2004, A Method for Simulating Transient Ground-Water Recharge in Deep Water-Table Settings in Central Florida by Using a Simple Water-Balance/Transfer Function Model. Scientific Investigations Report 2004-5195, U.S. Geological Survey, p. 49. [https://doi.org/10.3133/sir20045195]
• Park, Y., Choi, H.M. and Lee, J.Y., 2010, Fluctuation of water level and electric conductivity of groundwater influenced by typhoon. Journal of the Geological Society of Korea, 46, 633-645 (in Korean with English abstract).
• Theis, C.V, 1935, The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage. American Geophysical Union Transactions, 16, 519-524. [https://doi.org/10.1029/TR016i002p00519]
• Wikipedia contributors, 2020, Cluster analysis-Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Cluster_analysis&oldid=970190645, (July 30, 2020).
• Yi, M.J., Kim, G.B., Sohn, Y.C., Lee, J.Y. and Lee, K.K., 2004, Time Series Analysis of Groundwater Level Data Obtained from National Groundwater Monitoring Stations. Journal of the Geological Society of Korea, 40, 305-329 (in Korean with English abstract).
• Yoon, H., Yoon, P., Lee, E., Kim, G.B. and Moon, S.H., 2016, Application of machine learning technique-based time series models for prediction of groundwater level fluctuation to national groundwater monitoring network data. Journal of the Geological Society of Korea, 52, 187-199 (in Korean with English abstract). [https://doi.org/10.14770/jgsk.2016.52.3.187]
• Yoon, P., Yoon, H., Kim, Y. and Kim, G.B., 2014, A Comparative Study on Forecasting Groundwater Level Fluctuations of National Groundwater Monitoring Networks using TFNM, ANN, and ANFIS. Journal of Soil and Groundwater Environment, 19, 123-133 [https://doi.org/10.7857/JSGE.2014.19.3.123]