Arbitrary Lagrangian Eulerian 알고리즘과 격자 재구성 기법을 이용한 슬랩 분리에 관한 2차원 유한요소 수치 모형 개발
초록
지구 내부에서 발생하는 슬랩 분리 현상은 지진, 화산 생성, 지표 고도 상승에 영향을 미치는 중요한 지구동역학적 문제이다. 슬랩 분리 현상은 섭입한 슬랩이 강한 인장력을 받아 맨틀 내에서 여러 조각으로 잘리는 현상으로, 연속체 역학을 바탕으로 하는 유한요소법으로는 모사하기 어려운 것으로 알려져 있다. 이를 극복하기 위해 기존 연구에서는 슬랩 분리 현상을 모사하기 위해 입자 추적 방법을 도입했다. 본 연구에서는 COMSOL Multiphysics®에서 제공하는 ALE (Arbitrary Lagrangian Eulerian) 알고리즘과 격자 재구성 방법을 도입한 유한요소법을 이용하여 물질 사이 경계(예, 맨틀과 슬랩의 경계)를 직접 이류 시키는 방식의 2차원 슬랩 분리 모형을 개발했다. 우리가 구현한 슬랩 넥킹 모형은 20 Myrs 까지의 진화 양상과 넥킹 너비 변화율이 0이 되는 시점(~24 Myrs)의 기존 연구와의 오차율이 < ~3% 임을 확인하였다. 이는 ALE 방식을 이용한 슬랩 분리 수치 모사의 타당성을 정량적으로 입증한 것이다. 우리는 점성도가 일정한(등점성도) 슬랩 모형과 멱급수를 사용하여 변형률 속도에 따라 비선형적으로 점성도(멱급수 점성도)가 변하는 슬랩 모형을 제작하여 슬랩 침강속도, 넥킹 너비의 변화, 지표 고도 변화를 각각의 모형에서 탐구하고 비교했다. 두 모형은 현저하게 다른 넥킹 현상을 보여준다. 특히, 멱급수 점성도 넥킹 모형은 응력지수 n = 3.5-4에서 더 큰 집중정도와 빠른 넥킹 현상을 나타냈다. 반면, n = 4.5 인 경우 슬랩 넥킹 발생 속도 및 침강속도가 매우 느려 모형의 하부에 닿는데 ~230 Myrs의 시간이 필요하였다. 넓은 범위의 슬랩과 맨틀의 밀도 차이(25-250 kg/m3)와 점성도 차이(~103배 미만)를 적용하여 수치 실험을 진행하였다. 그 결과, 멱급수 점성도 넥킹 모형에서 n = 4일 때 슬랩의 침강속도는 ~3 cm/yr로 기존 결과와 유사함을 보였다. 지표 고도는 슬랩 분리 시점 이후로 0.5-2.5 km의 반등을 나타냈으며, 지표 고도 상승 속도는 0.025-0.36 mm/yr로 계산되었다. 이는 뉴 헤브리디스 섭입대에서 관찰된 슬랩 분리 이후 지표 상승 속도와 유사한 값이다.
Abstract
Slab detachment is one of the most enigmatic geodynamical problems in the Earth’s mantle, which affects volcanism, surface topography uplift, and seismicity. During the slab detachment, the subducting slab is fragmented into several pieces under strong extensional stress generated by resisting force from subduction of low-density structures (e.g., plateau, seamount, and continental crust). This detachment associated with severe deformation and even breaking-off has been considered difficult to be simulated using continuum mechanics such as finite element method (FEM). To overcome this limit of FEM, previous studies has adopted particle tracing method, which is successfully modeling the large distortion in the Lagrangian manner for investigating slab detachment. Another method to handle with large deformation in fluid dynamical approach is the ALE (Arbitrary Lagrangian Eulerian) algorithm in which the material boundaries (e.g., ambient mantle vs. slab) are directly advected by velocity field. In this study, we developed 2D FEM slab detachment model using the ALE and remeshing techniques implemented in the COMSOL Multiphysics®, and then benchmarked our models is different method from previous numerical studies (i.e., particle tracing). The general features of slab necking before 20 Myrs and the moment (~24 Myrs) for necking width change rate to converge zero are similar to previous numerical studies. This means that our model based on the ALE is accurate with error < ~3% accurate for simulating slab detachment. We quantitatively showed slab sinking velocity, necking width change, and surface topography change with the two end-member models; i.e., the constant viscosity and nonlinear viscosity (power-law viscosity) models. The two models showed prominently different style of necking. In particular, the slab with stress exponent n = 3.5-4 in power-law viscosity model showed much faster and more localized slab necking than that of constant viscosity model. On the other hand, the model with stress exponent n = 4.5 generated long time for slab necking (~230 Myrs). We tested a wide range of density (25-250 kg/m3) and viscosity (<~103) contrasts between the slab and mantle in the both models. Overall, we found that the slab sinking velocity is approximately 3 cm/yr when n = 4. The topography rebound of 0.5-2.5 km along the surface appears after slab detachment with the uplift rate of 0.025-0.36 mm/yr, which is in the range observed from the New Hebrides subduction zone.
Keywords:
slab detachment, ALE method, remeshing method, slab necking, stress exponent키워드:
슬랩 분리, Arbitrary Lagrangian Eulerian 방법, 격자 재구성 방법, 슬랩 넥킹, 응력지수1. 서 론
섭입하는 슬랩이 맨틀 내에서 잘리거나 찢어지는 현상인 슬랩 분리 현상(slab detachment, slab breakoff 및 slab tear 등)은 일반적으로 섭입하는 해양판 인근에 존재하는 상대적으로 낮은 밀도의 지구조체(예, 대륙지각과 해산 등)가 해구에 이르러 섭입에 저항하면서 발생한다(Sacks and Secor, 1990; Wortel and Spakman, 2000; Faccenna et al., 2006; Duretz et al., 2012). 이 저항력 때문에 맨틀 내부의 점성 슬랩에 인장력이 가해지면서 슬랩의 일부분이 집중적으로 가늘어지는 넥킹(necking)이 발생하고 이 현상이 심화하여 슬랩 분리로 발전하게 된다(Duretz et al., 2012). 슬랩 분리는 중발 지진(intermediate earthquakes)과 판내부 화산(intraplate volcanism)의 발생 기작 중 하나로 제시되고 있다(Obayashi et al., 2009; Tang et al., 2014). 특히, 해구와 멀리 떨어진 위치에 존재하는 판내부 화산 활동은 섭입한 슬랩의 분리된 틈으로 연약권의 맨틀 물질이 상승하여 일어날 수 있다. 몇몇 지진파 단층 촬영 연구에서는 슬랩 분리를 영상화 하였는데, 중앙 멕시코에 존재하는 중부 멕시코 횡단 화산대(Trans-Mexican Volcanic Belt; Ferrari, 2004)와 지중해의 카르파티아 산맥(Mediterranean-Carpathian region; Wortel and Spakman, 2000)에 관한 연구가 그 예이다. 슬랩 분리로 인해 발생하는 또 다른 지구동역학 현상인 지표 고도 상승(surface topography uplift)은 섭입된 슬랩의 일부분이 분리되면서 슬랩 자체 무게 감소에 의해 표면을 잡아당기는 슬랩 당김힘이 감소하여 발생한다. Chatelain et al. (1992)의 연구에서는 뉴 헤브리디스(New Hebrides) 하부의 맨틀에서 슬랩 분리가 일어났음을 지진원 분석을 통해서 파악했고, 슬랩 분리를 헤브리디스섬의 산호층 연대 측정을 통해 추정한 0.1-5 mm/yr의 지표 고도 상승과 연관 지었다.
판구조론적 관점에서 판 내부에 속하는 한반도와 북동 아시아 일원에서도 강력한 화산 분출의 역사가 있다(Yun and Lee, 2012). 특히, Tao et al. (2018)의 백두산 하부 지진파 단층 촬영 연구에서는 지하 660 km 근처에 분리된 두 고속도 이상(즉, 섭입된 차가운 태평양판) 사이에 존재하는 길이 ~200 km의 저속도 이상(즉, 뜨거운 맨틀 물질)을 발견하고 이를 슬랩 분리의 증거로 제시하여 분리된 틈으로 용승하는 뜨거운 맨틀 물질을 화산의 생성 원인으로 지목했다. 단층 촬영 기법에 바탕을 둔 기존 연구는 맨틀 내부 현상을 이해하는데 크게 기여했지만, 맨틀의 현재 상태에 관한 스냅숏을 보여주므로 슬랩 분리의 발생 시간과 발생 깊이 등의 동역학을 이해하기 위해서는 공간적/시간적 단위에 제약이 없는 수치 모사 기법이 필요하다. 컴퓨터의 수치 계산 능력 발달, 지구물리학적 자료 획득과 지구 내부 온도와 압력 조건 하의 암석/광물학 실험 결과를 바탕으로 파악한 맨틀과 암석권의 유동학적 물성(예, Karato, 2010)에 대한 이해를 바탕으로 슬랩 분리에 관한 수치 모사가 20세기 후반부터 급격히 발전했다(예, Stacey and Loper, 1988; Abbott et al., 1994) .
일반적으로 슬랩 분리에 관한 수치 모사는 오일러리안(Eulerian) 방식을 사용하며(Gurnis et al., 1996; Gerya et al., 2004), 이는 고정되어 있는 격자를 기준으로 연속체의 물리량(예, 밀도, 점성도, 속도장 등)을 계산하는 방법이다. 섭입 슬랩과 관련된 오일러리안 방식 바탕의 수치 모사 기법에서는 낮은 온도와 높은 점성도로 정의된 격자를 슬랩으로 가정하여 해석한다. 결과적으로, 슬랩과 맨틀 사이의 경계가 오일러리안 방식의 수치 모사에서는 모호하다. 가령, 특정한 온도를 기준으로 두 물질을 구분한다면, 확산(diffusion)에 의해서 분산된 열은 두 물질의 경계를 불명확하게 만든다. 열 확산도를 0으로 설정하면 이론적으로는 이류(advection)에 의해서만 열 이동이 발생하지만 이는 수치분산(numerical diffusion, Cheng et al., 1984)이라는 오차를 발생시켜 결과적으로 물질의 경계가 완벽하게 보존될 수는 없다. 슬랩과 맨틀의 경계가 명확하며 그 경계가 크게 변형하고 심지어 분리하는 현상을 다루는 슬랩 분리 연구(Gerya and Yuen, 2003; Gerya et al., 2004; Schmeling et al., 2008; Duretz et al., 2011)에서, 유체의 복잡한 대변형을 수치 모사하기 위해서 입자 추적 방법(particle tracing method)이 도입되었다. 이는 물성(예, 밀도, 점성도 등)에 관한 정보를 가지고 있는 입자를 속도장에 따라 흐르게 한 후 격자 내 포함된 입자의 종류와 갯수를 파악하여 그 격자의 물성을 갱신하는 기법이다. 유체의 복잡한 대변형을 모사하기 위한 방법에는 임의 라그랑지안 오일러리안 방법(Arbitrary Lagrangian Eulerian Method: 이하 ALE 방법)도 존재한다. 이 방법은 슬랩과 유체를 완전한 별개의 물질로 가정하고, 두 물질 사이의 경계 자체를 오일러리안 관점에서 계산한 속도장에 따라 이류시키는 방법이다. 본 연구에서 사용한 유한요소 소프트웨어인 COMSOL Multiphysics®(이하, COMSOL)에 ALE 방법을 도입하여 섭입대에서의 응력장과 표면 고도 변화를 계산하는 모형을 개발한 예는 있으나(Dasgupta and Mandal, 2018), ALE 바탕의 COMSOL이 슬랩 분리 수치 모사에 적용 가능한지 연구 및 평가된 적이 없다. 따라서, 우리는 입자 추적 방법을 사용한 기존 슬랩 분리 모사 연구(예, Schmalholz, 2011; Glerum et al., 2018)와는 다른 코드인 COMSOL에 ALE 방법을 도입하여 기존 연구와 비교 및 분석하였다.
슬랩이 자체 중력에 의해 맨틀 하부로 침강하게 되면 슬랩에 인장력이 발생하여 넥킹이 유도되고, 슬랩이 과하게 인장해 슬랩이 더 이상 스트레스 가이드(stress guide) 역할(즉, 심부에서 발생하는 응력을 표면에 전달해주는 능력)을 못할 때 슬랩 분리가 발생한다. 본 연구에서는 슬랩과 맨틀의 밀도 차이, 점성도 차이를 사용하여 슬랩 넥킹을 형성하고, 슬랩 분리가 발생하는 수치 모사를 COMSOL과 ALE를 이용해서 진행하였다. 슬랩의 점성도가 일정한 등점성도 넥킹 모형으로 슬랩의 침강속도, 시간에 따른 넥킹 너비, 슬랩 표면의 고도 변화를 탐구하였다. 특히, 넥킹 너비는 슬랩이 넥킹을 수반하며 침강할 때, 넥킹이 발생하는 지점의 슬랩 가로길이로 정의된다. 넥킹 너비의 시간에 따른 변화를 추적하면 넥킹 현상의 정도를 다양한 변수(밀도, 점성도 등)에 대해 정량화할 수 있다. 추가로 점성도가 변형률 속도(strain-rate)에 의존하여 슬랩의 점성도가 비선형적으로 변하는 멱급수 점성도 넥킹 모형을 사용하여 등점성도 넥킹 모형과 비교 및 분석했다. 우리는 수치 모사 실험 결과를 바탕으로 슬랩 분리 가능성을 판단하여 COMSOL의 슬랩 넥킹 모사 능력을 확인했다.
2. 실험 방법
2.1 지배방정식
본 연구에서는 지구 내부 물질인 맨틀을 비압축성 순수 점성 유체로 가정하고, 지배방정식으로 연속방정식(continuity equation; 식 1)과 스토크스 방정식(stokes equation; 식 2)을 사용하여 2차원 수치 모사를 진행하였다.
| (1) |
| (2) |
xi와 ui는 각각 i방향의 공간 좌표와 유체 흐름 속도로 정의한다. η, ρ, P, gi는 각각 유체의 점성도, 밀도, 압력, i방향의 중력가속도를 나타낸다. i=1과 2는 각각 수평 방향과 수직 방향을 의미한다. δij는 크로네커 델타(Kronecker delta)이다. 중력은 수직방향으로만 작용한다. 스토크스 방정식은 유체의 흐름을 주어진 η와 ρ를 이용해 속도장과 압력장을 도출하며, 본 연구에서는 슬랩의 다양한 밀도와 점성도를 대입하여 수치 모사를 진행하였다.
2.2 ALE와 격자 재구성 방법
본 연구에서는 격자(mesh)가 고정되어 물질 간 경계의 변형과 이동이 발생하지 않는 오일러리안(Eulerian) 방식을 도입했고, 이 단점을 보완하기 위해 격자를 유체의 속도장(velocity field)에 따라 변형 및 이동할 수 있도록 하는 기술인 ALE 방법을 도입하였다. ALE 방법에서는 속도장은 오일러리안 격자에서 구하고 격자 이동은 앞서 구한 속도장을 이용해서 라그랑지안 방식으로 물질 간 경계면의 변형과 이동을 모사한다. 또한 CFL 조건(Courant-Friedrichs-Lewy condition)에 따라 적절한 시간 단계(time-step) Δt를 구했다(예, Farhat et al., 2001). 물질을 둘러싼 닫힌 경계를 따라 앞서 구한 속도장과 Δt를 곱해 변위를 구해 식 (3)의 경계조건으로 대입한다. 경계 내부의 노드의 좌표 (X, Y)가 옮겨가는 새로운 좌표 (x, y)는 편미분 방정식 (3)을 풀어 구하며 이를 라플라스 스무딩(Laplace smoothing)이라고 한다.
| (3) |
라플라스 스무딩은 격자의 역전(mesh inverting)현상을 효과적으로 제거해준다(Löhner and Yang, 1996). 격자가 심하게 변형된 경우, 격자를 새로 만드는 격자 재구성 기술(remeshing)도 도입하였다. 본 연구의 수치 모사에서는 10회 미만의 격자 재구성을 하였다. ALE와 격자 재구성 방법을 도입할 때 횟수에 따른 오차를 확인하기 위해, 두 종류의 점성 유체를 정의한 모형을 이용해 간단한 시험을 수행했다. 그 결과, 10회의 격자 재구성을 수행해도 격자 재구성을 수행하지 않은 경우에 비해 0.5% 이하의 오차를 도출했다. 따라서, 격자 재구성 횟수는 모사 결과에 미미한 영향을 미치는 것으로 판단하였다(부록 1과 2 참조).
2.3 수치 모형의 구성
본 연구에서는 중력에 의한 암석권 자체의 무게로 인해 발생하는 슬랩 당김 힘(slab pull force)에 의해 자발적으로 암석권 슬랩이 침강하는 기존 수치 모사 연구(Schmalholz, 2011; Glerum et al., 2018)를 COMSOL을 이용하여 벤치마크하였다. 맨틀 영역의 길이는 1,000 km, 깊이는 660 km로 제작하였으며, 왼쪽과 오른쪽의 경계는 슬립없음(no slip)으로 지정하고, 하단의 경계는 자유 슬립(free slip)으로 지정하였다(그림 1). 암석권의 길이는 1,000 km, 깊이는 80 km이며, 슬랩의 깊이는 250 km, 너비는 80 km이고, 상단 경계는 자유 슬립으로 지정하였다(그림 1).

Model setup for 2D slab detachment. The slab is self-consistently deformed by gravitational body force. The model consists of lithosphere and mantle. The upper and lower boundaries are free slip and the left and right boundaries are no slip.
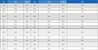
Model 1(그림 2-5)의 기본 물성은 맨틀과 암석권의 점성도가 변하지 않는 등점성도 넥킹 모형(constant viscosity necking model)으로 맨틀 점성도 ηm = 1021 Pa·s, 맨틀 밀도 ρm = 3,150 kg/m3이며, 암석권 점성도 ηL = 1023 Pa·s, 암석권 밀도 ρL = 3,300 kg/m3이다. ηL과 ρL의 값을 변화시켜 슬랩과 맨틀의 밀도 차이(Δρ = ρL - ρm)를 25-250 kg/m3, 슬랩의 맨틀에 대한 점성도 비율(R = ηL/ηm)을 10-1,000으로 설정하였다(표 1 참고). Model 2(그림 6-11)는 점성도가 일정한 맨틀과 멱급수(power-law) 점성도를 도입하여 변형률 속도에 따라 점성도가 비선형적으로 변하는 암석권을 가진 멱급수 점성도 넥킹 모형(power-law viscosity necking model)이다. 기본 물성은 등점성도 넥킹 모형과 동일하며, 멱급수 점성도(ηLP)는 식 (4)를 따른다(표 1 참고).
| (4) |
| (5) |
본 연구에서는 η0 = 1.75 - 9.75 × 1011 Pa· n = 3.5-4.5의 값으로 변화시키면서 계산을 진행하였다. (식 5)는 2차 변형률 속도 텐서 불변량(2nd invariant of strain-rate tensor; Schmalholz et al., 2008)이다. 는 계산이 진행되면서 위치와 시간에 따라 계속 변하지만, 지질학적으로 적합한 값인 10-15s-1-10-16s-1 (Beekman et al., 2012)을 식 (4)에 대입하면 암석권의 점성도는 1022-1024 Pa·s 사이 값으로 일반적 지구동역학 수치 모사에 사용되는 값과 유사하다(Ramsay and Pysklywec, 2011). 슬랩의 최소 점성도 값은 1021 Pa·s으로 맨틀 점성도 값보다 작지 않게 설정하였으며, 슬랩의 최대 점성도는 일반적인 수치 모사에 사용되는 최대 값인 1024 Pa·s로 설정하였다(표 1 참조).
본 연구에서는 병렬화된 COMSOL 5.3 소프트웨어를 사용하고, 코어(core) 64개, 램(RAM) 512 GB 인 하드웨어를 활용하여 수치해석을 진행하였다. 모든 모형 영역에 0.2-13 km의 요소 크기를 가지는 삼각형 요소를 사용하였으며, 유한요소 방법의 이산화 결과인 희소 행렬을 병렬 역산하기 위해 MUMPS (MUtifrontal Massively Parallel Sparse) 솔버(solver)를 이용하였다. 최대 13,000개의 요소를 사용했고, 격자 재구성 기술을 10회 미만으로 수치 모사를 진행하였다. 각 수치 모형의 계산 시간은 1시간 미만이다.
3. 결 과
맨틀과 암석권의 점성도가 변하지 않는 등점성도를 이용한 모형(Model 1; 그림 2-5)과 맨틀은 점성도가 일정하게 설정하고 암석권에는 멱급수 점성도를 도입한 모형(Model 2; 그림 6-11)을 바탕으로 넥킹을 수치 모사했다.
3.1 Model 1: 등점성도 넥킹 모형
Model 1은 ρm = 3,150 kg/m3, ηm = 1021 Pa·s로 고정ηm시키고 암석권(슬랩, slab)의 밀도와 점성도만 변화시킨 등점성도 넥킹 모형으로, 슬랩과 맨틀의 밀도 차이(Δρ= ρL - ρm; 회색 화살표)와 슬랩의 맨틀에 대한 점성도 비율(R = ηL/ηm; 빨간 화살표)을 변화시킨 다수의 계산 결과 도출된 값을 도시하였다(그림 2). 시간 = 14 Myrs까지 계산을 진행하고, 슬랩이 하단 경계에 접근하면 경계 효과가 발생하므로, 깊이 640 km에 슬랩이 도달하면 계산을 중지하도록 설정했다. Δρ = 50 kg/m3, R = 63이면, 슬랩은 ~350 km 깊이까지 침강하였으며, 슬랩과 맨틀 경계 부근의 는 ~10-15s-1로 슬랩의 변형이 작아 눈에 띄는 넥킹이 발생하지 않은 것을 확인하였다(그림 2g). 반면, R 값은 동일하고 Δρ = 250 kg/m3인 모형에서 슬랩은 ~630 km 깊이까지 침강하고, 확연한 슬랩 넥킹이 발생하였으며, 넥킹이 발생한 부근의 는 ~10-14s-1이다(그림 2i). 이는 슬랩과 맨틀의 밀도 차이와 슬랩의 침강속도, 슬랩의 넥킹 발생이 서로 양의 상관관계가 있음을 지시한다(그림 2g, 2h, 2i 비교). Δρ = 250 kg/m3, R = 160 일 때, 슬랩은 ~400 km 깊이까지 침강하고, 뚜렷한 슬랩 넥킹이 발생하지 않았다(그림 2c). 이는 R 값이 작을수록 더욱 강한 변형집중(strain localization)이 발생하여 넥킹을 유도할 수 있음을 의미한다(그림 2c, 2f, 2i를 비교).

2nd invariant of strain-rate tensor at Time = 14 Myrs calculated from constant viscosity necking models with different values of Δρ and R. The horizontal and vertical arrows represent the directions of increasing Δρ and R, respectively. The cases with (a) Δρ = 50 kg/m3 and R = 160, (b) Δρ = 150 kg/m3 and R = 160, (c) Δρ = 250 kg/m3 and R = 160, (d) Δρ = 50 kg/m3 and R = 100, (e) Δρ = 150 kg/m3 and R = 100, (f) Δρ = 250 kg/m3 and R = 100, (g) Δρ = 50 kg/m3 and R = 63, (h) Δρ = 150 kg/m3 and R = 63, and (i) Δρ = 250 kg/m3 and R = 63.
R과 Δρ가 슬랩 끝단의 시계열 위치 변화에 미치는 영향을 파악하기 위해서 R = 100와 Δρ = 150 kg/m3에 고정시킨 후 수치 모사를 진행하였다(각각, 그림 3a와 3b). R = 100으로 고정되어 있고, Δρ = 25 kg/m3(그림 3a 파란색선)과 Δρ = 250 kg/m3 (그림 3a 주황색선)을 적용하면, 슬랩이 ~640 km 깊이까지 가라앉는 시간은 각각 ~190 Myrs와 ~20 Myrs이다. = 25 kg/m3에서 = 250 kg/m3으로 10배 증가하면, 슬랩이 가라앉는 시간은 ~1/10배로 감소하여 슬랩 평균 침강속도 Vsink가 ~10배 빨라지며, 이는 Δρ와 Vsink가 양의 상관관계에 있음을 지시한다 (그림 3a). 반면 Δρ = 150 kg/m3으로 동일하고, R = 1,000(그림 3b 검은색선)과 R = 100(그림 3b 보라색선)으로 서로 다른 R 값을 적용하면, 슬랩이 ~ 640 km 깊이까지 가라앉는 시간은 각각 ~270 Myrs와 ~30 Myrs이다. 이는 R이 커질수록 슬랩의 변형이 적게 일어나고 Vsink가 느려지는 것을 의미한다(그림 3b). 가로축과 세로축이 각각 Δρ와 Vsink인 그래프에서(그림 3c), R의 값이 작을수록, Δρ가 클수록 침강속도가 빠르다.

The temporal change of position of slab lower tip and slab sinking velocity Vsink with different values of R and Δρ. (a) The cases with fixed values of R = 100 and Δρ = 25-250 kg/m3 . (b) The cases with fixed value of Δρ = 150 kg/m3 and varying R = 10-1000 (c) Vsink depending on Δρ. The horizontal and vertical axes are Δρ and Vsink, respectively. The red shaded zone refers to realistic range of Δρ in actual nature.
지진파 속도 구조를 이용하여 밀도 구조를 역산한 기존 연구에서는 맨틀의 구성성분, 온도 등으로 인해 밀도 차이가 50 - 150 kg/m3 범위라고 제시하고 있으며(Maystrenko and Scheck-Wenderoth, 2009), 해당 밀도 차이에서 본 연구의 슬랩 침강속도는 4 cm/yr이하이다(그림 3c의 붉은색 음영 부분). 침강 속도는 슬랩의 인장만으로 결정되고, 슬랩 당김 힘이 표면에 존재하는 암석권에 전달은 되지만 슬랩이 수직으로 존재하기 때문에 표면 암석권의 수평운동은 비교적 작아(예, R = 10, Δρ = 150 kg/m3인 경우 <0.8 cm/yr) 고려하지 않았다.
섭입하는 슬랩에 넥킹 발생 시, 슬랩의 넥킹 너비(necking width; 그림 4a)와 집중정도(그림 4b)에 Δρ가 미치는 영향을 도시하였다(그림 4). 슬랩이 넥킹을 수반하면서 침강할 때 넥킹이 발생한 슬랩의 최소 너비를 넥킹 너비로 정의하였으며, 넥킹 집중정도는 슬랩 최대 너비/최소 너비로 정의하여 같은 시간에 집중정도가 클수록 넥킹이 더 강하게 발생하였음을 지시한다. R = 1,000으로 고정하고 Δρ = 50 kg/m3 (그림 4a 파란색선)인 경우, 슬랩이 ~100 Myrs 동안 침강하면서 슬랩 너비는 80 km에서 ~75 km까지 감소하며 이는 집중정도 = ~1.05(그림 4b 파란색선)에 해당한다. 반면 Δρ = 150 kg/m3 (그림 4a 빨간색선)일 때, 슬랩 너비가 80 km에서 ~62 km까지 감소하는 시간은 100 Myrs이며, 집중정도 = ~1.12(그림 4b 빨간색선)이다. 이는 Δρ가 클수록 더욱 강한 집중이 발생하여 넥킹 발생 속도가 빠르다는 것을 의미한다.

Necking width and degree of localization in constant viscosity necking model. (a) Necking width varies with time in the cases of Δρ = 50-250 kg/m3 . (b) Degree of localization depends on Δρ. The higher Δρ is applied, the higher the degree of localization emerges, which indicates the faster slab necking.
슬랩이 침강하고 넥킹의 집중정도가 최대가 될 때 슬랩 분리가 발생할 수 있으며, 슬랩 분리 과정에서 분리된 슬랩의 자체 무게 감소에 의해 표면의 반등(rebound)을 유도 할 수 있다. 슬랩 분리에 의해서 표면 고도의 반등이 발생한 사례가 뉴 헤브리디스 지역(New Hebrides)에서 보고된바 있다(Chatelain et al., 1992). Δρ = 150 kg/m3, R = 100 일 때, 슬랩이 침강하며 유도되는 표면 전체의 고도 변화를 시간에 따라 그림 5a에 도시하였는데, 그래프의 가로축은 암석권의 길이(length)이고 세로축은 표면 고도이다. 시간 = 25 Myrs (그림 5a 초록색선)에서 표면 고도는 ~4.5 km 깊이까지 침강하였으며, 이 시간 이후 고도가 반등하는 것을 확인하였다. 이는 ~25 Myrs 시점 전후에 슬랩 분리가 발생했음을 암시한다. R 값의 변화에 따른 점 I (그림 5a 빨간색 점)과 점 II (그림 5a 파란색 점)의 고도를 시간에 따라 도시하여(각각, 그림 5b와 5c), 슬랩이 표면과 맨틀 심부 사이의 응력을 전달해주는 스트레스 가이드 역할을 하지 못하는 분리 시점(detachment time) 이후 표면의 고도가 급격하게 변하는 것을 확인하였다. 점 I과 II의 좌표는 각각 표면의 중심점과 중심에서 ~120 km 떨어진 위치에 설정했다. Δρ = 150 kg/m3으로 고정되어 있고 R = 250을 정의하면(그림 5b와 5c), ~60 Myrs의 분리 시점 직전에 점 I의 고도는 ~5.2 km 깊이까지 침강하였으며 이후에 고도가 반등하였고(그림 5b 빨간색선), 점 II는 ~0.8 km 높이까지 상승한 후 분리 시점 직후 급격하게 침강하였다(그림 5c 빨간색선). R이 증가하여 슬랩이 기계적으로 더 강한 경우 넥킹이 발생하는 시간이 더 오래 걸리는 것을 확인하였다(그림 5b와 5c의 파란색과 빨간색선 비교). 반면 R = 100으로 고정시키고 Δρ의 변화에 따른 넥킹 시간을 도시한 그래프에서(그림 5d와 5e), Δρ = 100 kg/m3 (그림 5d와 5e 빨간색선)일 때 분리 시점은 ~40 Myrs이다. 점 I의 고도는 ~3 km 깊이까지 침강한 후 분리 시점 이후에 반등하였으며(그림 5d 빨간색선), 점 II의 고도는 ~0.45 km깊이까지 상승한 후 침강하였다(그림 5e 빨간색선). Δρ가 클수록 표면 중심점(즉, 점 I)의 더 큰 침강고도, 점 II의 더 큰 상승고도를 유도할 뿐만 아니라, 분리 시점이 역시 더 빠른 것을 확인했다. 다양한 Δρ와 R 값을 사용한 다수의 모형에서 표면의 점 I과 II의 고도를 측정한 결과, 슬랩 바로 위 지점의 고도 침강이 < 10 km이고, 점 II의 고도 상승이 < 1 km이며, 이는 실제 해구(trench)와 벌지(bulge)의 고도와 유사하다(Chatelain et al., 1992; Westaway, 1993; Buiter et al., 2002).

Surface topography in constant viscosity model. (a) The surface topography in the model with Δρ = 150 kg/m3 and R = 100 along the surface at different time = 1-33 Myrs. The surface topography rebounds right after detachment time (~25 Myrs). We tracked the elevation two Points I (red circle) and II (blue circle). The temporal change of Points I (b) and II (c) in the cases of Δρ = 150 kg/m3 and R = 100-1000. The small leads to earlier necking and rebound. The temporal change of Points I (d) and II (e) in the case of Δρ = 50 kg/m3 - 150 kg/m3 and R = 100. The large density contrast is a favorable condition for fast necking and its subsequent rebound.
3.2 Model 2: 멱급수 점성도 넥킹 모형
그림 6은 슬랩의 유동학적 성질에 멱급수 법칙 점성도(power-law viscosity)를 적용하여 점성도가 변형률 속도(strain-rate)에 따라 비선형적으로(식 4 참조) 변하는 Model 2의 전반적 수치 모사 결과이다. 맨틀 밀도 ρm과 점성도 ηm, 슬랩 밀도 ρL, 슬랩 초기 점성도에 관한 η0, n을 각각 3,150 kg/m3, 1021 Pa·s, 3,300 kg/m3, 4.75 × 1011 Pa·, 4로 설정한 모형에서 시간에 따른 넥킹 너비(그림 6a)와 슬랩과 맨틀의 점성도(η; 그림 6b-e), 2차 변형률 속도 텐서 불변량(; 그림 6f-i), 폰 미세스 (von Mises) 응력(τv = 2η; 그림 6j-m)의 변화를 도시하였다. 기존 연구(그림 6a의 녹색 점선과 파란색 점선)와 본 연구(그림 6a의 빨간색 실선)를 비교해보면, ~20 Myrs 시간까지는 넥킹 너비가 같은 양상으로 감소하는 것을 확인할 수 있다(그림 6a). 그러나, 시간이 ~21 Myrs가 되면 슬랩이 맨틀 하단 경계에 가까워져 경계효과가 나타나고, 경계효과가 발현되는 방식은 수치 계산 소프트웨어마다 다르기 때문에 경계 근처에서 넥킹 너비의 시간 변화는 완전히 같을 수 없는 것으로 판단된다. 실제로 기존 연구(Schmalholz, 2011; Glerum et al., 2018)는 물질의 이류를 유한요소법에 입자 추적 방법을 도입하여 모사했다. 반면, 우리 연구에서는 ALE 방법을 유한요소에 결합하여 경계의 이류를 계산하였다. 하지만 넥킹 너비의 감소가 급격하게 느려지는 시기가(~21 Myrs) 비슷하며, 넥킹 너비가 유지되기 시작하는 시점은 24 Myrs로 비슷한 양상을 갖기 때문에 본 연구에서 사용한 COMSOL로도 슬랩 넥킹 모사가 가능하다고 판단된다. 뿐만 아니라 두 기존 연구에서 슬랩이 하단 경계에 가까워졌을 때 넥킹 너비 차이가 최대 ~2 km 이며, 본 연구와 기존 연구의 넥킹 너비 차이의 오차가 최대 3%를 넘지 않아 유사하다고 판단하였다. 시간 = 15 Myrs에서, 넥킹이 발생하기 시작한 부분의 너비는 ~50 km이며(그림 6a), ηLP가 ~1023 Pa·s (그림 6c)로 슬랩 내 다른 부위의 비해 현저히 작다. 는 ~10-15s-1 (그림 6g)로 주변보다 크다. τv는 ~108 Pa (그림 6k)로 넥킹 부분이 주변보다 더 큰 응력을 받아 넥킹이 발생하기 시작하였다. 슬랩이 침강하면서 넥킹 너비가 감소하고 넥킹 너비가 최소인 시간 = 25 Myrs에서 넥킹 너비는 ~10 km (그림 6a)이다. 시간 = ~20 Myrs 전후에 넥킹 너비가 시간에 따라 비선형적으로 감소하는 것이 확인되어 이 시기 전후로 슬랩 분리가 발생 할 수 있음을 나타낸다.
슬랩 끝단의 시계열 위치가 Δρ, η0값에 따라 변화하는 양상을 파악하기 위해서, n = 4에 고정시킨 후 수치 모사를 진행하였다(그림 7a-c). η0 = 4.75 × 1011 Pa·, n = 4로 고정되어 있고, Δρ = 25 kg/m3 (그림 7a 연보라색선)와 Δρ = 250 kg/m3 (그림 7a-b의 파란색선)일 때, 슬랩이 ~640 km 깊이까지 가라앉는 시간은 각각 ~1,600 Myrs와 ~8 Myrs이다. Δρ가 10배 증가하면, 슬랩의 끝단이 660 km 바닥에 닿는데 걸리는 시간은 1/200 배 이상 짧아져 비선형적으로 감소함을 파악할 수 있다. 반면, Δρ = 150 kg/m3, n = 4로 고정되어 있고, η0 = 4.75 × 1011 Pa· (그림 7c 연두색선)인 슬랩이 640 km 깊이까지 가라 앉는 시간은 ~25 Myrs이며, η0 = 9.75 × 1011 Pa·인 경우(그림 7c 진한회색) ~170 Myrs이다(그림 7c). Vsink를 도시한 그래프에서(그림 7d), Δρ = 150 kg/m3으로 이고, η0 = 2.75 × 1011 Pa· (그림 7d 파란색선)와 η0 = 4.75 × 1011 Pa· (그림 7d 연두색선)에서 Vsink는 각각 ~3 cm/yr와 ~1 cm/yr이다. 멱급수 점성도 넥킹 모형에서는 Vsink가 비선형적으로 증가하며, η0가 작을수록 Δρ에 따른 Vsink의 변화 폭이 큰 것으로 판단된다.

(a) Comparison of necking width change with Schmalholz (2011) and Glerum et al. (2018). Temporal change of (b-e) viscosity (f-i) 2nd invariant of strain rate tensor, and (j-m) von Mises’s stress.

The temporal change of position of slab lower tip and slab necking velocity Vsink with different values of η0 and Δρ. (a-b) The cases with fixed value of η0 = 4.75 ×1011 Pa·s1n, n = 4 and Δρ = 25-250 kg/m3 . (c) The cases with fixed value of Δρ = 150 kg/m3 , n =4 and Δρ = 1.75-9.75 ×1011 Pa·s1n . (d) Vsink depending on Δρ, η0. The red shaded zone refers to realistic rang of Δρ in actual nature.
변형이 지속됨에 따라 비선형적으로 점성도가 감소하는 멱급수 점성도 넥킹 모형에서 슬랩의 넥킹 너비와 집중정도에 Δρ가 미치는 영향을 도시하였다(그림 8). η0 = 4.75 × 1011 Pa·, n = 4로 고정되어 있고 Δρ = 50 kg/m3 (그림 8a 파란색선) 일 때, 슬랩 너비가 처음 500 Myrs 동안은 선형적으로 감소하지만, 그 후 600 Myrs까지는 ~10 km까지 비선형적으로 감소하여 집중정도 = ~4에 이른다 (그림 8c 파란색선). 반면 Δρ = 250 kg/m3 인 경우(그림 8b 연두색선) 슬랩이 10 Myrs 동안 침강하면서 슬랩 너비가 ~10 km까지 감소하며 이는 집중정도 = ~5.5에 해당한다(그림 8d 연두색선). Δρ = 150 kg/m3, η0 = 4.75 × 1011 Pa·, n = 4일 때 슬랩의 초기 점성도는 1024 Pa·s이며(그림 8b 모형), 넥킹 너비는 10 km까지 ~25 Myrs 시간동안 감소하고(그림 8b 빨간색선), 집중정도 = ~5.2를 나타낸다(그림 8d 빨간색선). Δρ = 150 kg/m3, R = 1,000(즉, 슬랩의 점성도가 1024 Pa·s)이면(그림 4), 넥킹 너비는 250 Myrs 시간동안 30 km까지만 감소하며(그림 4a 빨간색선), 집중정도는 1.8이다(그림 4b 빨간색선). 이는 멱급수 점성도 넥킹 모형이 등점성도 넥킹 모형보다 더 강한 집중이 발생하여 넥킹을 유도할 수 있음을 지시한다.

Transient change of necking width and degree of localization of power-law viscosity necking models (η0 = 4.75 ×1011 Pa·s1n and n = 4). (a) The change of necking width with different values of Δρ = 50-250 kg/m3 . (b) The zoomed-up zone of Time = 0-90 Myrs from Fig. 8a. (c) The degree of localization derived from Figs. 8a and 8b, respectively.
멱급수 점성도 넥킹 모형에서 슬랩이 표면과 심부의 응력을 전달해주는 스트레스 가이드 역할을 하지 못하게 되는 분리 시점에서 표면의 고도 상승을 도시하고(그림 9a), 표면의 중심점과 플랭크 지점에서의 표면 고도를 Δρ와 η0값의 변화에 따라 도시하였다(그림 9b-e). Δρ = 150 kg/m3, η0 = 4.75 × 1011 Pa·으로 설정하면, 표면 고도는 18 Myrs의 시간에 ~3.5 km 깊이까지 침강하며(그림 9a 검은색선), 18 Myrs 시간 이후에는 고도가 반등하기 때문에 이 시간을 분리 시점으로 지정하고, 이 시점 전후에 슬랩 분리가 발생했음을 지시한다. 점 I (그림 9a 빨간색 점)과 점 II (그림 9a 파란색 점)를 각각 표면의 중심점과 중심에서 120 km 떨어진 위치에 존재하도록 설정하여, η0값의 변화에 따른 점 I과 점II의 고도를 도시하고 분리 시점을 확인하였다(그림 9b-c). Δρ = 150 kg/m3으로 고정되어 있고 η0 = 4.75 × 1011 Pa·로 적용하면(그림 9b-c), 18 Myrs의 분리 시점에서 점 I의 고도는 ~3.5 km 깊이까지 침강하였으며 이후에 고도가 반등하였고(그림 9b 연두색선), 점 II는 ~1.3 km 높이까지 상승한 후 다시 침강하였다(그림 9c 연두색선). η0가 감소하여 슬랩이 기계적으로 더 약한 경우 분리 시점이 더 빠르다는 것을 확인하였다. 반면 η0 = 4.75 × 1011 Pa·으로 고정시키고 Δρ의 변화에 따른 넥킹 시간을 도시한 그래프에서(그림 9d-e), Δρ = 100 kg/m3일 때 분리 시점은 ~70 Myrs이다(그림 9d-e 빨간색선). 점 I의 고도는 ~3 km 깊이까지 침강한 후 분리 시점 이후에 반등하였으며(그림 9d 빨간색선), 점 II의 플랭크의 고도는 ~0.7 km 깊이까지 상승한 후 다시 침강하였다(그림 9e 빨간색선). Δρ가 클수록 점 I에서는 더 깊은 침강 깊이, 점 II에서는 더 높은 상승을 유도할 뿐 아니라, 분리 시점도 더 빠른 것을 확인했다. 멱급수 점성도 넥킹 모형은 변형률 속도 의존성 연화 현상이 존재하기 때문에 등점성도 넥킹 모형에 비해 슬랩의 변형의 정도가 크다. 변형의 정도가 더 크다는 것은 멱급수 점성도 넥킹 모형이 등점성도 넥킹 모형에 비해 슬랩에 작용하는 응력이 크다는 것을 지시한다. 따라서 분리 시점 이후 응력의 변화가 큰 멱급수 점성도 넥킹 모형에서 슬랩 분리가 발생한 후의 표면 고도 변화가 더 뚜렷하다. 등점성도 넥킹 모형(그림 5a)의 분리 시점 전후로 표면 중심점에서는 ~1 km정도 반등하였다. 반면 멱급수 점성도 넥킹 모형(그림 9a)에서는 표면 중심점이 ~2 km 반등했다.

Surface topography in power-law model. (a) The surface topography in the model with Δρ = 150 kg/m3 , η0 = 4.75 ×1011 Pa·s1n and n = 4 along the surface at different time = 6-25 Myrs. The surface topography rebounds right after detachment time at ~18 Myrs). We tracked the elevation two Points I (red circle) and II (blue circle). The temporal change of Points I (b) and II (c) in the cases Δρ = 150 kg/m3 , and η0 = 2.75 ×1011 Pa·s1n - 4.75 ×1011 Pa·s1n . The temporal change of Points I (d) and II (e) in the case of Δρ = 50 kg/m3 - 150 kg/m3 and η0 = 4.75 ×1011 Pa·s1n .
Δρ = 150 kg/m3, η0 = 4.75 × 1011 Pa·으로 고정하고, 응력지수 n 값(각각 3.5, 4, 4.5; 회색 화살표)과 시간(빨간색 화살표)에 따라 동적으로 변화하는 점성도를 도시 했다(그림 10). 슬랩이 하단 경계에 접근하면 경계 효과가 발생하므로 깊이 640 km 지점에서 계산을 중지하도록 설정하였다. 응력지수 n의 값을 3.5, 4, 4.5로 정의하면 640 km 깊이까지 슬랩이 도달하는 시간은 각각 7.5 Myrs, 25 Myrs, 230 Myrs으로 n값에 따라 비선형적으로 증가하였다(각각 그림 10g, 10h, 10i). n = 3.5이고 시간 = 7.5 Myrs에서(그림 10g) 넥킹 너비가 최소가 되는 지점의 점성도는 ~1022 Pa·s 이며, n = 4.5이고 시간 = 230 Myrs에서(그림 10i) 슬랩의 점성도가 최소가 되는 부분은 ~이고 슬랩 넥킹이 존재하는 부분은 일부에 불과하다. 값이 작을수록, 기계적 강도가 변형률 속도에 더 민감하여 약화 현상이 더 활발하기 때문에 점성도가 더 빠르게 감소하고 넥킹의 발생 시점도 빠르다는 것을 의미한다.

Power-law viscosity necking models with different stress exponent n = 3.5 (left column), 4 (middle column), and 4.5 (right column). The horizontal and vertical arrows are indicating changes of n and time, respectively. The values of Δρ and η0 are fixed at Δρ = 50 kg/m3 η0 and = 4.75 ×1011 Pa·s1n , respectively. If is relatively small value, the viscosity is reduced quickly (compare Figs. 10g and 10i).
멱급수 점성도 넥킹 모형에서 응력지수 n 값의 차이에 따른 슬랩 끝단 위치(그림 11a), 넥킹 너비(그림 11b), 집중정도(그림 11c)를 도시하였다. Δρ = 150 kg/m3, η0 = 4.75 × 1011 Pa·으로 고정시키고 n의 값을 3.5-4.5로 0.1의 간격씩 차이를 두고 수치 모사를 진행하였다. n = 4.0(그림 11a 보라색선)와 n = 4.5(그림 11a 남색)일 때 슬랩이 ~640 km 깊이까지 가라앉는 시간은 각각 ~49 Myrs와 ~230 Myrs이며, 이 시점에 각각 넥킹 너비는 80 km에서 ~10 km까지 감소하였다(각각 그림 11b 파란색선과 남색선). 이는 n값이 커지면 슬랩이 경계부근까지 침강하는 시간이 증가하고 슬랩 침강속도, 넥킹 너비가 감소하는 시간이 느리다는 것을 의미한다. n값이 비교적 작은 경우(3.5-4.0; 그림 11c) 집중정도 = 5.0-5.5에 해당하지만, n값이 비교적 큰 경우(4.1-4.5; 그림 11c) 집중정도 = 3.0-5.0이다. 이는 n이 작을수록 더욱 강한 변형 집중이 발생하여 넥킹 발생 속도가 빠르다는 것을 지시한다.
4. 토론 및 결론
본 연구에서는 유한요소 소프트웨어인 COMSOL을 사용하여 복잡한 대변형 문제인 슬랩 분리 수치 모사를 성공적으로 수행하였다. 대변형 현상을 모사하기 위해 입자 추적 방법을 도입한 기존 수치 모사연구(Schmalholz. 2011; Glerum et al., 2018)와 다르게 우리는 ALE 알고리즘과 격자 재구성(remeshing)을 조합한 방법을 도입하였다. 우리는 멱급수 점성도 넥킹 모형에서 넥킹 너비가 일정한 시간(~20 Myrs)까지 기존 연구와 같은 양상으로 감소하는 것을 확인하였다. 기존 연구에서 사용한 입자 추적 방법은 입자가 가지고 있는 정보(예, 점성도, 밀도 등)를 입자가 위치한 각 요소에서 추출하고, 입자의 위치와 물성을 내삽하여 각 요소의 물성을 갱신한다. 하지만 격자 재구성을 수반하는 ALE 방법에서는 격자 재구성을 진행 하기 전에 각 절점의 정보를 추출하고, 재구성 후에 새롭게 구성 된 격자에 물성을 내삽하여 갱신한다. 이와 같이 입자 추적방법과 ALE 방식 사이의 근본적인 차이로 인해서 같은 유한요소법에 바탕을 둔 수치 계산 소프트웨어라고 해도 경계효과가 발현되는 방식이 상이하여 하단 경계 근처에서 넥킹 너비의 시계열 변화는 완전히 같을 수는 없는 것으로 판단된다. 하지만 넥킹 너비 변화율이 0에 수렴하기 시작하는 시간이 ~24 Myrs로 유사하여 본 연구에서 활용한 유한요소 소프트웨어 패키지 COMSOL을 슬랩 넥킹 모사에 이용할 수 있음을 확인하였다. 차후, 슬랩의 강도에 영향을 줄 수 있는 마찰열(frictional heating) 또는 전단열(shear heating)과 같은 기계적 열 발생 효과를 우리 모형에 추가하는 등의 추가 연구가 필요하다고 판단된다.
본 연구에서 재현한 멱급수 점성도 넥킹 모형은 맨틀의 밀도와 점성도는 일정하며 슬랩의 점성도가 변형률 속도에 의존하는 모형이다. 슬랩의 점성도는 전위 크리프(dislocation creep) 응력지수 n 값에 따라 변형률 속도에 의존하며, 멱급수 점성도는 실제 자연의 암석 점성도를 현실적으로 매개화할 수 있음이 다수의 크리프 실험을 통해 확인되었다(예, Evans and Goetze, 1979; Katayama and Karato, 2008). 기존 지구동역학 수치 모사 연구(Funiciello et al., 2003)에서는 계산 편의를 위해 슬랩의 점성도를 일정한 상수로 두고 진행하였다. 그에 비해 본 연구에서는 슬랩의 점성도가 일정한 등점성도 넥킹 모형과 변형률 속도 의존성 연화 현상이 존재하는 멱급수 점성도 넥킹 모형을 비교 분석하였다. 그 결과, 등점성도 넥킹 모형과 멱급수 점성도 넥킹 모형의 슬랩 침강속도, 넥킹 너비의 변화, 지표 고도 변화의 양상이 상이함을 확인하였다. 두 모형의 가장 큰 차이는 넥킹 너비가 감소하는 정도와 그에 따른 침강속도다. 등점성도 넥킹 모형에 비해 멱급수 점성도 넥킹 모형은 변형률 속도 의존성 연화 현상이 존재하여 슬랩의 점성도가 시계열에 따라 비선형적으로 감소한다. n 값에 따라 결과 차이는 있으나 밀도 차이와 초기 점성도가 같을 때 멱급수 점성도 넥킹 모형의 침강속도가 최대 ~10배 빠른 것을 확인하였다.
넥킹 너비와 집중정도를 확인하여 멱급수 점성도 넥킹 모형과 등점성도 넥킹 모형의 수치 계산 결과를 비교하였다. 넥킹 너비의 감소가 현저하게 발생하고, 이 현상이 심화하여 슬랩 분리가 발전하게 되는데(Duretz et al., 2012), 본 연구에서의 등점성도 넥킹 모형에서는 넥킹의 집중정도가 낮다. 초기 밀도 차이와 초기 점성도 차이가 등점성도 넥킹 모형과 같을 때, 집중정도가 현저히 크다. 이는, 멱급수 점성도 넥킹 모형에서 더 강한 변형 집중이 발생하여 넥킹을 유도할 수 있음을 지시한다. 실제 자연에서는 슬랩 분리 현상이 활발하게 발생하고 있는데 등점성도 모형으로는 이 현상을 적절하게 모사할 수 없으며, 멱급수 점성도 모형을 사용해야 슬랩 분리와 그에 수반하는 지구물리학적 현상을 모사할 수 있다.
슬랩 표면의 고도 변화를 관찰하여 분리 시점 이후 표면 고도 반등이 이루어졌음을 확인하였다. 슬랩 분리 이후 표면 고도 반등은 0.5-2.5 km이며, 이는 기존 수치 연구와 매우 유사함을 확인하였다(예, Buiter et al., 2002). 또한 기존의 뉴 헤브리디스 지역에 산호층 연대 측정을 통해 추정한 0.1-5 mm/yr 의 지표 고도 상승 속도(Chatelain et al., 1992)는 본 연구의 0.025-0.36 mm/yr 와 비슷한 차수를 가지며, 지질학적 자료를 바탕으로 한 수치 모사를 통해 슬랩 분리의 발생 깊이와 시점을 추정할 수 있을 것으로 판단된다.
암석 변형 실험을 통해 도출한 응력지수 n 값은 3-5 이며(예, Karato and Weidner, 2008; Karato, 2010), 본 연구의 멱급수 점성도 넥킹 모형에서는 n = 3.5-4.5의 값을 적용하여 수치 모사를 수행했다. 값이 비교적 작은 n = 3.5-4.0과 비교적 큰 n = 4.1-4.5이 적용된 멱급수 점성도 모형은 각각 5.0-5.5와 3.0-5.0의 집중정도를 보였다. 이는 n의 값이 작을수록 더욱 강한 변형 집중이 발생하고 넥킹 발생 속도가 빠르다는 것을 의미한다. 즉 n의 값이 작을수록 기계적 강도가 변형률 속도에 더 민감하여 약화 현상이 더 활발하므로, 점성도가 더 빠르게 감소하고 넥킹 발생 시점이 빠르다는 것을 의미한다. 따라서 실제 자연에서도 응력지수 값이 비교적 작은 경우에 넥킹이 발생할 것이라고 판단된다. n 값은 주로 광물의 종류(예, 감람석의 n = 3.5; Hirth and Kohlstedt, 2004, 석영의 n = 4.0 ± 0.9; Gleason and Tullis, 1995)와 물의 양(예, 수화 감람석의 n = 2.5; Mackwell et al., 1985, 수화 석영의 n = 2.6; Kronenberg and Tullis, 1984)에 의해 결정되기 때문에 슬랩 분리의 시점과 표면 지구조에 미치는 영향을 정량화하기 위해서는 슬랩의 유동학적 구조 (예, 해양지각의 두께, 슬랩에 포함되어 있는 대륙 지각의 두께, 물의 양 등)에 관한 정보가 필수적이다. 특히 최근 Nakajima et al. (2009)의 지진파 단층 촬영 연구에서는 지구 심부에 섭입된 슬랩의 해양지각과 맨틀의 함수화 정도를 시각화하였으며, 함수 정도에 따라 n 값을 조절하는 방식으로 본 연구에 적용하여 더 정확한 슬랩 분리를 모사할 수 있을 것으로 판단된다.
전 세계적으로 섭입 혹은 해령 등 판 경계에서 먼 곳에 위치하는 화산이 다수 존재한다(Ferrari, 2004; Zhao et al., 2009; Nelson and Grand, 2018; Dielforder et al., 2019). 이러한 화산들은 판 내부 화산(intraplate volcanoes)으로 분류하며, 한반도 북동쪽에 존재하는 백두산 역시 판 내부 화산이라고 판단된다(Zhao et al., 2004; Lei and Zhao, 2005; Tang et al., 2014). 백두산은 지난 2000년간 동아시아에서 발생한 화산활동 중 가장 격렬한 화산활동으로 기록되고 있다(Yun et al., 1993; Yun and Lee, 2012). 백두산은 생성 기원에 대해 지질학적, 지화학적으로 많은 연구가 진행되어 왔으며(Choi et al., 2006; Chen et al., 2007; Zou et al., 2008), 슬랩이 섭입하는 과정에서 발생하는 탈수화 작용과 스테그넌트 슬랩 위의 거대 맨틀 쐐기(Big Mantle Wedge)의 대류순환 때문에 발생한 것으로 여겨져 왔다. 해양 지각 혹은 섭입 해양판 상부에서 수화된 맨틀이 구석 유동(corner flow)에 의해 맨틀 상전이대로 물을 공급 할 수 있음을 제시하였고(Maruyama and Okamoto, 2007; Ikemoto and Iwamori, 2014), 맨틀 상전이대에서의 슬랩 분열이 탈수 작용에 영향을 미칠 수 있다고 주장하였다(Motoki and Ballmer, 2015). 하지만 Green et al. (2010)의 연구에서는 섭입하는 슬랩이 맨틀 상전이대(410-660 km)에서 함수 광물과 함께 물을 운반하는 것은 맨틀의 온도와 압력 조건을 고려하면 매우 어려운 현상이며, 따라서 660 km 근처에서는 슬랩의 탈수 작용이 발생하지 않을 것이라고 주장했다. 특히 최근의 고 해상도 지진파 단층 촬영 연구(Tang et al., 2014; Tao et al., 2018)에서는 백두산 하부의 상전이대에서 슬랩 분리를 발견하고 그 틈으로 용승한 맨틀을 백두산 생성 원인이라고 제시했다. 하지만, 일반적으로 슬랩 분리는 섭입대와 가까운 거리(100-200 km)정도, 깊이 ~350 km이내에서 발생하는 것으로 알려져 있다(Gerya et al., 2004; Obayashi et al., 2009; Burkett and Billen, 2010; Duretz et al., 2011). 그에 비해, 백두산 하부의 슬랩 분리는 섭입대와 거리가 멀고(~1,000 km), 깊은 곳에서 발생하였다. 슬랩 넥킹과 슬랩 분리의 물리적 타당성을 타진하기 위해서 본 연구에서 재현한 멱급수 점성도 넥킹 모형을 활용하고, 나아가 다양한 변수(마찰열, 전단열, 약대 등)를 사용하여 깊은 깊이에서 발생하는 슬랩 분리와 그에 따른 맨틀 물질의 용승에 의한 화산 생성 연구에 본 연구를 적극 활용할 수 있을 것으로 기대된다.
Acknowledgments
본 연구는 한국연구재단의 대통령POST_DOC펠로우쉽(NRF-2014R1A6A3A04055841), 행정안전부 ‘방재안전분야 전문인력 양성’ 사업과 기상청 기상·지진See-At기술개발사업(KMI2018-02110), 신진연구지원 사업(NRF-2019R1C1C1010804)의 지원으로 수행되었습니다.
References
-
Abbott, D., Drury, R., Smith, W.H.F. and Drury, R., 1994, Flat to steep transition in subduction style. Geology, 22, 937-940.
[https://doi.org/10.1130/0091-7613(1994)022<0937:FTSTIS>2.3.CO;2]

-
Beekman, F., Bull, J.M., Cloetingh, S. and Scrutton, R.A., 2012, Crustal fault reactivation facilitating lithospheric folding/buckling in the central Indian Ocean. Geological Society of London, 99, 251-263.
[https://doi.org/10.1144/GSL.SP.1996.099.01.19]

-
Buiter, S.J., Govers, R. and Wortel, M., 2002, Two-dimensional simulations of surface deformation caused by slab detachment. Tectonophysics, 354, 195-210.
[https://doi.org/10.1016/S0040-1951(02)00336-0]

-
Burkett, E.R. and Billen, M.I., 2010, Three‐dimensionality of slab detachment due to ridge‐trench collision: Laterally simultaneous boudinage versus tear propagation. Geochemistry, Geophysics, Geosystems, 11, Q11012.
[https://doi.org/10.1029/2010GC003286]

-
Chatelain, J.., Molnar, P., Prévot, R. and Isacks, B., 1992, Detachment of part of the downgoing slab and uplift of the New Hebrides (Vanuatu) Islands. Geophysical Research Letters, 19, 1507-1510.
[https://doi.org/10.1029/92GL01389]

-
Chen, Y., Zhang, Y., Graham, D., Su, S. and Deng, J., 2007, Geochemistry of Cenozoic basalts and mantle xenoliths in Northeast China. Lithos, 96, 108-126.
[https://doi.org/10.1016/j.lithos.2006.09.015]

-
Cheng, R.T., Casulli, V. and Milford, S.N., 1984, Eulerian-Lagrangian Solution of the Convection-Dispersion Equation in Natural Coordinates. Water Resources Research, 20, 944-952.
[https://doi.org/10.1029/WR020i007p00944]

-
Choi, S.H., Mukasa, S.B., Kwon, S. and Andronikov, A.V., 2006, Sr, Nd, Pb and Hf isotopic compositions of late Cenozoic alkali basalts in South Korea: Evidence for mixing between the two dominant asthenospheric mantle domains beneath East Asia. Chemical Geology, 232, 134-151.
[https://doi.org/10.1016/j.chemgeo.2006.02.014]

-
Dasgupta, R. and Mandla, N., 2018, Surface topography of the overriding plates in bi-vergent subduction systems: A mechanical model. Tectonophysics, 746, 280-295.
[https://doi.org/10.1016/j.tecto.2017.08.008]

-
Dielforder, A., Frasca, G., Brune, S. and Ford, M., 2019, Formation of the Iberian-European Convergent Plate Boundary Fault and Its Effect on Intraplate Deformation in Central Europe. Geochemistry, Geophysics, Geosystems, 20, 2395-2417.
[https://doi.org/10.1029/2018GC007840]

-
Duretz, T., Gerya, T.V. and May, D.A., 2011, Tectonophysics Numerical modelling of spontaneous slab breakoff and subsequent topographic response. Tectonophysics, 502, 244-256.
[https://doi.org/10.1016/j.tecto.2010.05.024]

-
Duretz, T., Schmalholz, S.M. and Gerya, T.V., 2012, Dynamics of slab detachment. Geochemistry, Geophysics, Geosystems, 13, 1-17.
[https://doi.org/10.1029/2011GC004024]

-
Evans, B. and Goetze, C., 1979, The temperature variation of hardness of olivine and its implication for polycrystalline yield stress. Journal of Geophysical Research: Solid Earth, 84, 5505-5524.
[https://doi.org/10.1029/JB084iB10p05505]

-
Faccenna, C., Bellier, O., Martinod, J., Piromallo, C. and Regard, V., 2006, Slab detachment beneath eastern Anatolia: A possible cause for the formation of the North Anatolian fault. Earth and Planetary Science Letters, 242, 85-97.
[https://doi.org/10.1016/j.epsl.2005.11.046]

-
Farhat, C., Geuzaine, P. and Grandmont, C., 2001, The discrete geometric conservation law and the nonlinear stability of ALE schemes for the solution of flow problems on moving grids. Journal of Computational Physics, 174, 669-694.
[https://doi.org/10.1006/jcph.2001.6932]

-
Ferrari, L., 2004, Slab detachment control on mafic volcanic pulse and mantle heterogeneity in central Mexico. Geology, 32, 77-80.
[https://doi.org/10.1130/G19887.1]

-
Funiciello, F., Morra, G., Regenauer-Lieb, K. and Giardini, D., 2003, Dynamics of retreating slabs; 1. Insights from two-timensional numerical experiments. Journal of Geophysical Research: Solid Earth, 108, 1-17
[https://doi.org/10.1029/2001JB000898]

-
Gerya, T.V. and Yuen, D.A., 2003, Rayleigh-Taylor instabilities from hydration and melting propel ‘cold plumes’ at subduction zones. Earth and Planetary Science Letters, 212, 47-62.
[https://doi.org/10.1016/S0012-821X(03)00265-6]

-
Gerya, T.V., Yuen, D.A. and Maresch, W.V., 2004, Thermomechanical modelling of slab detachment. Earth and Planetary Science Letters, 226, 101-116.
[https://doi.org/10.1016/j.epsl.2004.07.022]

-
Gleason, G.C. and Tullis, J., 1995, A flow law for dislocation creep of quartz aggregates determined with the molten salt cell. Tectonophysics, 247, 1-23.
[https://doi.org/10.1016/0040-1951(95)00011-B]

-
Glerum, A., Thieulot, C., Fraters, M., Blom, C. and Spakman, W., 2018, Nonlinear viscoplasticity in ASPECT: benchmarking and applications to subduction. Solid Earth, 9, 267-294.
[https://doi.org/10.5194/se-9-267-2018]

-
Green II, H.W., Chen, W.-P. and Brudzinski, M.R., 2010, Seismic evidence of negligible water carried below 400-km depth in subducting lithosphere. Nature, 467, 828-831.
[https://doi.org/10.1038/nature09401]

-
Gurnis, M., Eloy, C. and Zhong, S., 1996, Free-surface formulation of mantle convection-II. Implication for subduction-zone observables. Geophysical Journal International, 127, 719-721.
[https://doi.org/10.1111/j.1365-246X.1996.tb04050.x]

-
Hirth, G. and Kohlstedt, D., 2004, Rheology of the Upper Mantle and the Mantle Wedge: A View from the Experimentalists. Inside the subduction Factory, 138, 83-105.
[https://doi.org/10.1029/138GM06]

-
Ikemoto, A. and Iwamori, H., 2014, Numerical modeling of trace element transportation in subduction zones: implications for geofluid processes. Earth, Planets and Space, 66, 26.
[https://doi.org/10.1186/1880-5981-66-26]

-
Karato, S., 2010, Rheology of the Earth’s mantle: A historical review. Gondwana Research journal, 18, 17-45.
[https://doi.org/10.1016/j.gr.2010.03.004]

-
Karato, S. and Weidner, D.J., 2008, Laboratory studies of rheological properties of minerals under deep-mantle conditions. Elements, 4, 191-196.
[https://doi.org/10.2113/GSELEMENTS.4.3.191]

-
Katayama, I. and Karato, S., 2008, Effects of water and iron content on the rheological contrast between garnet and olivine. Physics of the Earth and Planetary Interiors, 166, 57-66.
[https://doi.org/10.1016/j.pepi.2007.10.004]

-
Kronenberg, A.K. and Tullis, J., 1984, Flow strengths of quartz aggregates: Grain size and pressure effects due to hydrolytic weakening. Journal of Geophysical Research: Solid Earth, 89, 4281-4297.
[https://doi.org/10.1029/JB089iB06p04281]

-
Lei, J. and Zhao, D., 2005, P-wave tomography and origin of the Changbai intraplate volcano in Northeast Asia. Tectonophysics, 397, 281-295.
[https://doi.org/10.1016/j.tecto.2004.12.009]

-
Löhner, R. and Yang, C., 1996, Improved ALE mesh velocities for moving bodies. Communications in numerical methods in engineering, 12, 599-608.
[https://doi.org/10.1002/(SICI)1099-0887(199610)12:10<599::AID-CNM1>3.0.CO;2-Q]

-
Mackwell, S., Kohlstedt, D. and Paterson, M., 1985, The role of water in the deformation of olivine single crystals. Journal of Geophysical Research: Solid Earth, 90, 11319-11333.
[https://doi.org/10.1029/JB090iB13p11319]

-
Maruyama, S. and Okamoto, K., 2007, Water transportation from the subducting slab into the mantle transition zone. Gondwana Research, 11, 148-165.
[https://doi.org/10.1016/j.gr.2006.06.001]

-
Maystrenko, Y. and Scheck-wenderoth, M., 2009, Density contrasts in the upper mantle and lower crust across the continent - ocean transition: constraints from 3-D gravity modelling at the Norwegian margin. Geophysical Journal International, 179, 536-548.
[https://doi.org/10.1111/j.1365-246X.2009.04273.x]

-
Motoki, M.H. and Ballmer, M.D., 2015, Intraplate volcanism due to convective instability of stagnant slabs in the mantle transition zone. Geochemistry, Geophysics, Geosystems, 16, 538-551.
[https://doi.org/10.1002/2014GC005608]

-
Nakajima, J., Hirose, F. and Hasegawa, A., 2009, Seismotectonics beneath the Tokyo metropolitan area, Japan: Effect of slab-slab contact and overlap on seismicity. Journal of Geophysical Research, 114, 1-23.
[https://doi.org/10.1029/2008JB006101]

-
Nelson, P.L. and Grand, S.P., 2018, Lower-mantle plume beneath the Yellowstone hotspot revealed by core waves. Nature Geoscience, 11, 280.
[https://doi.org/10.1038/s41561-018-0075-y]

-
Obayashi, M., Yoshimitsu, J. and Fukao, Y., 2009, Tearing of stagnant slab. Science, 324, 1173-1175.
[https://doi.org/10.1126/science.1172496]

-
Ramsay, T. and Pysklywec, R., 2011, Anomalous bathymetry, 3D edge driven convection, and dynamic topography at the western Atlantic passive margin. Journal of Geodynamics, 52, 45-56.
[https://doi.org/10.1016/j.jog.2010.11.008]

-
Sacks, P.E. and Secor, D.T., 1990, Delamination in collisional orogens. Geology, 18, 999-1002.
[https://doi.org/10.1130/0091-7613(1990)018<0999:DICO>2.3.CO;2]

-
Schmalholz, S.M., 2011, A simple analytical solution for slab detachment. Earth and Planetary Science Letters, 304, 45-54.
[https://doi.org/10.1016/j.epsl.2011.01.011]

-
Schmalholz, S.M., Schmid, D.W. and Fletcher, R.C., 2008, Evolution of pinch-and-swell structures in a power-law layer. Journal of Structural Geology, 30, 649-663
[https://doi.org/10.1016/j.jsg.2008.01.002]

-
Schmeling, H., Babeyko, A.Y., Enns, A., Faccenna, C., Funiciello, F., Gerya, T. and Golabek, G.J., 2008, A benchmark comparison of spontaneous subduction models - Towards a free surface. Physics of the Earth and Planetary Interiors, 171, 198-223.
[https://doi.org/10.1016/j.pepi.2008.06.028]

-
Stacey, F.D. and Loper, D.E., 1988, Thermal history of the Earth: a corollary concerning non-linear mantle rheology. Physics of the Earth and Planetary Interiors, 53, 167-174.
[https://doi.org/10.1016/0031-9201(88)90139-2]

-
Tang, Y., Obayashi, M., Niu, F., Grand, S.P., Chen, Y.J., Kawakatsu, H., Tanaka, S., Ning, J. and Ni, J.F., 2014, Changbaishan volcanism in northeast China linked to subduction-induced mantle upwelling. Nature Geoscience, 7,470.
[https://doi.org/10.1038/ngeo2166]

-
Tao, K., Grand, S.P. and Niu, F., 2018, Seismic Structure of the Upper Mantle Beneath Eastern Asia From Full Waveform Seismic Tomography. Geochemistry, Geophysics, Geosystem, 19, 2732-2763.
[https://doi.org/10.1029/2018GC007460]

-
Westaway, R., 1993, Quaternary uplift of southern Italy. Journal of Geophysical Research: Solid Earth, 98, 21741-21772.
[https://doi.org/10.1029/93JB01566]

-
Wortel, M.J. and Spakman, W., 2000, Subduction and slab detachment in the Mediterranean-Carpathian region. Science, 290, 1910-1917.
[https://doi.org/10.1126/science.290.5498.1910]

-
Yun, S. and Lee, J.H., 2012, Analysis of Unrest Signs of Activity at the Baegdusan Volcano. The Journal of the Petrological Society of Korea, 21, 1-12 (in Korean with English abstract).
[https://doi.org/10.7854/JPSK.2012.21.1.001]

- Yun, S.H., Won, C.K. and Lee, M.W., 1993, Cenozoic Volcanic Activity and Petrochemistry of Volcanic Rocks in the Mt. Paektu Area. Journal of Geological Society of Korea, 29, 291-307 (in Korean with English abstract).
-
Zhao, D., Lei, J. and Tang, R., 2004, Origin of the Changbai intraplate volcanism in Northeast China: Evidence from seismic tomography. Chinese Science Bulletin, 49, 1401-1408
[https://doi.org/10.1360/04wd0125]

-
Zhao, D., Tian, Y., Lei, J., Liu, L. and Zheng, S., 2009, Seismic image and origin of the Changbai intraplate volcano in East Asia: Role of big mantle wedge above the stagnant Pacific slab. Physics of the Earth and Planetary Interiors, 173, 197-206.
[https://doi.org/10.1016/j.pepi.2008.11.009]

-
Zou, H., Fan, Q. and Yao, Y., 2008, U-Th systematics of dispersed young volcanoes in NE China: asthenosphere upwelling caused by piling up and upward thickening of stagnant Pacific slab. Chemical Geology, 255, 134-142.
[https://doi.org/10.1016/j.chemgeo.2008.06.022]

Appendix
Appendix 1. Carbon Emission of Labeled Interior Products
격자 재구성을 도입할 때 격자 재구성 횟수에 따른 오차를 확인하기 위해 다음과 같은 실험을 진행하였다. 깊이 60, 길이 10인 점성 매질의 55 지점에 유체 상태인 반지름 0.5인 원을 설정하고, 중력에 따라서 자유 낙하 시켜 종단속도(terminal velocity)를 측정하였다. 매질과 원의 점성도는 모두 1이며, 밀도는 각각 1과 2로 지정하였다. 종단 속도에 도달하기에 충분하도록 계산 시간은 2로 설정했다.
Appendix 2. Error of terminal velocity of falling circle depending on number of remeshing.
격자 재구성 방법을 사용하지 않았을 때 종단 속도는 0.764이며, 격자 재구성 방법을 1, 5, 10회 진행한 경우 종단 속도는 각각 0.765, 0.767, 0.766 이다. 격자 재구성 횟수가 0회인 경우 대비 종단 속도의 오차는 0.5%에 불과하다. 본 연구에서는 대부분의 수치 모사에서 10회 미만의 격자 재구성을 실시하였다.