
모멘트 텐서 역산 방법을 이용한 2017 포항지진 진원 깊이의 지각속도모델 의존성 연구
초록
2017년 규모 5.4의 포항지진은 국내에서 본격적인 계기 관측이 시작된 1978년 이후 가장 큰 피해를 초래한 지진이다. 포항지진이 2016년 발생한 규모 5.8의 경주지진보다 더 큰 피해를 낳은 이유 중 하나는 얕은 진원 깊이 때문이다. 최근 연구 결과에 따르면 포항지진의 진원 깊이는 2 ~ 10 km인데, 포항지진이 주변에 위치한 지열발전소에 의한 유발 지진인지 여부를 분명히 파악하기 위해서는 진원 깊이를 정확하게 측정하는 것이 필요하다. 주로 진원 깊이 측정에 사용되는 주시를 사용할 경우 지각속도 모델과 진원 깊이 간에 상충효과(trade-off)가 발생하여 정확한 진원 깊이를 계산하는 데에 어려움이 있다. 따라서 이 연구에서는 주시 자료가 아닌 파형 자료를 사용한 모멘트 텐서 역산 방법을 통해 진원 깊이를 측정하고자 한다. 주시 자료를 사용할 때처럼 상충효과가 큰 지 알아보기 위해 8개의 지각속도 모델을 적용하여 지각모델에 따른 불확실성을 정량적으로 측정하고자 하였다. 이 연구의 결과 다양한 지각속도 모델을 사용하여도 약 3 ~ 5 km의 일정한 진원 깊이가 측정됐고, 이는 진앙과 약 500 m 거리에 위치한 지열발전소의 지열정들의 깊이(각각 4.215 km와 4.340 km)와 매우 유사함을 알 수 있었다.
Abstract
The 2017 Pohang earthquake (ML 5.4) is the most devastating earthquake in South Korea since modern seismometers were installed in 1978. One of the reasons why the Pohang earthquake caused more damage than the 2016 Gyeongju earthquake with ML 5.8 is due to its shallow focal depth. The focal depth of the Pohang earthquake is estimated to be between 2 ~ 10 km according to recent studies. It is necessary to quantitatively measure the exact focal depth of the Pohang earthquake because it is closely related to whether the Pohang earthquake is induced by the nearby enhanced geothermal system site or not. Travel times usually used in the estimation of focal depths suffer from the trade-off between crustal velocity models and focal depths, hampering accurate estimation of focal depths. Therefore, we applied moment tensor inversion method to waveforms from the Pohang earthquake to estimate focal depth. Furthermore, to estimate the trade-off between crustal velocity models and focal depths quantitatively, we used 8 different crustal velocity models. Our results show stable estimations of focal depth of about 3 ~ 5 km regardless of crustal models, which is very similar to the water injection depth of 4.215 and 4.340 km.
Keywords:
moment tensor inversion, 2017 Pohang earthquake, crustal velocity model, focal depth, induced earthquake키워드:
모멘트 텐서 역산, 포항지진, 지각속도 모델, 진원 깊이, 유발 지진1. 서 론
2017년 11월 15일 한반도 남동부 지역에서 발생한 규모 5.4의 포항지진은 1978년 국내에서 본격적인 지진계기 관측이 시작된 이래 피해가 가장 많이 발생한 지진이다. 포항지진에 의해 이재민은 1,945명, 그리고 총 재산피해는 약 850억원의 피해가 발생했다(Ministry of the Interior and Safety, 2017). 2016년 발생한 규모 5.8의 경주지진보다 더 큰 피해를 초래한 가장 큰 원인 중 하나는 진원 깊이 차이 때문인데, 최근 연구결과에 따르면 진원 깊이가 약 13.5 km (KIGAM, 2016) ~ 15 km (KMA, 2016)인 경주지진보다 포항지진의 진원 깊이는 2 ~ 10 km로 상대적으로 더 얕게 측정되었다. 하지만 포항지진의 진원 깊이는 연구자에 따라 다르게 측정되었고, 이에 따른 해석이 분분하여 과연 포항지진이 주변 지열발전소의 영향으로 인한 유발 지진인지에 대한 정확한 분석이 필요한 실정이다. Kim et al. (2018)은 포항 지열발전소 부근 3 km 이내에 있는 8개의 간이 지진계 자료를 사용한 주시 역산을 통해 포항지진 본진의 진원 깊이를 4.5 km로 측정했으며, 이는 주변 지열발전소의 지열정 하부깊이와 비슷해 지열발전소에 의해 유발된 지진이라 제안한 바 있다. 반면, Chung et al. (2018)는 7개의 지각속도 모델과 120 km 이내의 기상청 관측소를 이용하여 P파와 S파의 초동을 사용한 진원 재결정 역산을 통해 6 ~ 11.5 km 구간의 깊이를 산출하고, 지온 해석에 근거해 본진의 진원 깊이를 7 km로 제안한 바 있다. 또한, 포항지진 분석 보고서(KMA, 2018)에서는 6개의 지각속도 모델과 P파와 S파의 도달 시간을 이용해 HYPOINVERSE-2000 (Klein, 2007)과 HypoDD (Waldhauser and Ellsworth, 2000)로 진원 깊이를 결정했고, 15 km 이내 관측소를 사용했을 때 2 ~ 5 km, 50 km 이내 관측소를 사용했을 때 7 ~ 10 km로 본진 진원 깊이가 결정되었다고 보고된 바 있다. 이에 비해 파형 비교를 통해 진원을 구한 Grigoli et al. (2018)의 결과는 4.0 km였고 모멘트 텐서 역산을 통해서는 4.5 km의 결과를 얻었다. 포항 지역 지각속도 모델을 탄성파 탐사 및 시추공 관측소의 음파 검층 자료 등을 이용해 계산한 뒤 많은 자료를 사용하여 정밀한 결과를 얻은 정부조사연구단(Geological Society of Korea, 2019)의 결과는 4.27 km였다. 위 언급한 진원 깊이에 관한 연구들 중 일부는 지진 자료의 주시를 이용한 역산 방법을 적용했다. 이 방법의 단점은 탄성파 탐사 등 다른 방법을 통해 지각속도를 정밀하게 미리 알고 있지 않다면, 주어진 속도모델에서의 지각속도에 따라 진원 깊이가 다르게 계산될 수 있는 상충효과(trade off)가 생길 수 있기에 적용된 속도모델에 따라 다른 결과를 얻을 수 있다는 점이다. 이에 반해 모멘트 텐서 역산은 파형 자료를 주로 사용하는데 이 경우 상충효과가 어느 정도 존재하는지 정량적인 측정은 아직 시도되지 않았다.
이 연구에서는 포항지진 본진의 진원 깊이를 측정하기 위해 파형 자료를 사용하여 모멘트 텐서 역산을 수행하였고 상충효과를 정량적으로 살펴보기 위해 서로 다른 8개의 지각속도모델을 사용하였다. 여기서 주시를 통해 구한 진원 깊이와 모멘트 텐서 역산을 통해 구한 진원 깊이가 다를 가능성이 있다. 왜냐하면, 주시 자료를 사용할 경우에는 파열이 시작된 지점에 대한 진원 깊이를 구하지만, 모멘트 텐서 역산을 통한 진원 깊이는 사용된 주파수 영역에서 가장 많은 에너지가 발산된 깊이를 측정하기 때문이다. 그러나 포항 지진이 규모 5.4의 중규모 지진이고 이 정도의 규모는 점원(point source)으로 자주 근사되는 것을 감안하면, 이 연구에서는 두 방법을 통해 측정한 진원 깊이가 동일한 것으로 가정하도록 한다. 또한, 모멘트 텐서 분석을 통해 포항지진 본진의 진원 깊이뿐 아니라 지진 발생에 있어 유체의 영향이 어느 정도인지 비 이중짝힘(non-double-couple, non-DC)함량을 측정함으로써 유추해 보고자 한다. 그리고 역산에 사용된 주파수 영역을 다양한 범위에서 시도해봄으로써 가장 좋은 결과를 얻을 수 있는 적절한 주파수 영역을 찾아보도록 한다.
2. 배경이론
이 연구에서 사용하는 모멘트 텐서 역산은 다음과 같은 과정을 통해 이루어진다(Aki and Richards, 2002). 주어진 위치와 시간에 발생한 점원(point source)에 의한 변위 u(t)는 모멘트 텐서 M과 그린함수 G의 공간에 대한 미분을 사용하여 식 (1)과 같이 나타낼 수 있다.
| (1) |
모멘트 텐서 M은 식 (2)와 같이 6개의 기본적인 텐서 Mi의 선형적인 결합으로 나타낼 수 있다.
| (2) |
기본적인 텐서 Mi의 6개 요소는 식 (3)과 같다. 여기서 M1부터 M5까지의 텐서는 이중짝힘(double-couple, DC) 진원 기구를 나타내고, M6은 등방원 (isotropic source, ISO)을 의미한다. 유체 흐름의 영향으로 인해 주로 발생하는 보상선벡터 쌍극자(Compensated Linear Vector Dipole, CLVD)의 진원 기구는 DC 진원 기구의 조합으로 나타낼 수 있다.
| (3) |
따라서 모멘트 텐서(M)는 MISO+MDC+MCLVD의 형태로 나타낼 수 있고, 여기서 MISO는 등방원에 의한 모멘트 텐서, MDC는 DC에 의한 모멘트 텐서, MCLVD는 CLVD에 의한 모멘트 텐서를 의미한다. 식 (1)과 (2)를 함께 사용하면, 식 (4)로 나타낼 수 있다.
| (4) |
| (5) |
| (6) |
| (7) |
이는 a에 대한 과대결정 선형 역산 문제(over-determined linear inverse problem)가 되고, 식 (8)과 같이 최소자승법(least-squares method)을 사용하여 풀 수 있다.
| (8) |
여기서 aopt는 행렬 a의 최적값이며, ET은 행렬 E의 전치행렬이다. 그리고 합성 파형(s)은 최소자승법으로 구한 aopt를 이용해 식 (9)와 같이 나타낼 수 있다.
| (9) |
3. 지진자료 선택
이 연구에 사용된 관측소와 지진 위치 정보는 그림 1과 같다. 포항지진이 발생한 지역에서 근거리에 있는 관측소를 사용하기 위해 기상청 국가지진종합정보시스템(http://necis.kma.go.kr)과 한국지질자원연구원 지진연구센터(https://quake.kigam.re.kr)의 지진파 자료를 이용했다.
또한, 방위각 보정 값 및 계기 보정 정보를 알 수 없는 관측소를 제외하고, 진북 배열이 되어있어 방위각 보정이 필요 없는 2015년 이후 신설한 기상청 시추공 관측소와 Lee and Sheen (2015)을 통해 방위각 보정값을 알 수 있는 관측소를 이용했다. 따라서 기상청(CHYB, CIGB, GDDB, GUWB, JEJB, YEYB, YOCB, YODB, YOJB, YUSB) 관측소 자료와 한국지질자원연구원(GKP1) 관측소 자료를 사용해 총 11개의 관측소 자료를 이용했다.
4. 지각 속도모델
모멘트 텐서 역산 방법이 다양한 지각모델에 대해 어느 정도의 불확실성을 갖는지 확인하기 위해 8개의 지각모델을 이용했다(그림 2). 사용된 지각모델은 한반도 지각 속도모델인 Kim (1995), Chang and Baag (2006), Kim et al. (2011)과 전 지구 속도모델인 IASP91 (Kennett and Engdahl, 1991), 그리고 최근 발표된 포항지진 정부조사연구단 요약보고서에 이용된 정부조사연구단 지각 속도모델(Geological Society of Korea, 2019) 등 5개의 속도모델을 포함한다. 정부조사연구단 지각 속도모델은 포항 지열발전소 부근에서 측정된 탄성파 탐사 및 시추공 관측소의 음파 검층 자료 등을 이용해 약 7 km 깊이까지의 지각 속도모델을 5개의 층으로 나눠 결정하였고, 그 이상 깊이에 대한 지각 속도모델은 Kim et al. (2011) 모델의 하부 영역과 결합하여 만든 모델이다. 같은 방식으로 정부조사연구단이 사용한 천부 지각의 5개 층과 다른 지각 속도모델(Kennett and Engdahl, 1991; Kim, 1995; Chang and Baag, 2006)의 하부 영역을 결합한 새로운 모델 3개를 만들어 더 총 8개의 지각속도 모델을 사용했다.
5. 모멘트 텐서 역산
이 연구에서는 모멘트 텐서 역산 방법을 사용하기 위해 ISOLA 소프트웨어를 사용했다. ISOLA는 포트란과 매트랩 기반으로 만들어진 소프트웨어이며, 모멘트 텐서 역산을 할 뿐만 아니라 결과, 연구지역 지도 등을 나타낼 수 있는 유용한 기능이 있다. ISOLA에 대한 자세한 설명 및 사용법 등은 Sokos and Zahradnik (2008, 2013)에 기술되어 있다.
non-DC 성분의 함량비를 측정하기 위해 DC, CLVD 그리고 ISO 성분을 모두 포함하는 전 모멘트 텐서 역산(full moment tensor inversion)을 수행했고, 또한 모델 파라미터의 개수를 줄여 좀 더 안정적인 해를 구하기 위해 포항지진의 본진이 순수한 편차 응력(deviatoric stress)으로 인해 발생한 지진으로 간주하여 ISO 성분을 제외하고 DC와 CLVD의 영향만을 고려한 편차 모멘트 텐서 역산(deviatoric moment tensor inversion)도 수행했다. 진앙 위치는 포항지진 정부조사연구단 요약 보고서(Geological Society of Korea, 2019)에서의 값이 정확하다는 가정 하에 이 연구에서의 역산은 진원 깊이와 진원 시간의 최적 지점을 격자 탐색 방법(grid search)을 통해 찾는다. 이는 식 (10)에 의해 계산된 관측 파형(u)과 합성 파형(s)의 상호상관(Corr)이 최대가 되는 지점으로 결정된다(그림 3, 4 참조).

A grid search result of 15 source positions with 0.5 km intervals and 41 time shifts with 0.15 second intervals. Each point has a focal mechanism and the red focal mechanism is the point with the highest correlation value.

Correlation values between synthetic and observed waveforms using focal mechanisms obtained at various depths. The 15 focal mechanisms are obtained along the y-axis direction of the diagram in Fig. 3, on which the red focal mechanism is located.
| (10) |
여기서 이고, k는 관측소 개수, j는 방향 성분을 나타낸다. 이렇게 계산된 상호상관이 최대가 되는 지점에서의 진원 깊이(km), 진원 기구해, 단층면 해(°), DC 함량(%) 그리고 입력 진원 시간으로부터의 시간 변동(time shift, sec) 결과가 출력된다.
이 연구에서는 3 ~ 10 km의 진원 깊이를 0.5 km 간격으로, 시간 변동은 기준 진원 시간으로부터 -3 ~ +3 초를 0.15 초 간격으로 나누어 격자 탐색 방법을 적용하여 계산하였다.
6. 신뢰성 평가요소
모멘트 텐서 역산에서 상호상관이 최대가 되는 지점에서 얻어진 결과들이 과연 신뢰할만한 결과인가를 평가하는 기준을 정하는 것이 필요하다. 이 연구에서는 Sokos and Zahradnik (2013)의 방법을 따라 다음과 같은 5개의 지표들을 사용하여 결과의 신뢰성을 평가하고자 한다.
첫 번째, 신호 대 잡음 비(Signal to Noise Ratio, SNR)는 지진파의 P파 초동 시간을 기준으로 계산되며, P파 이전의 잡음과 P파 이후 신호의 비율을 측정한다. 이 값이 클수록 신뢰도가 높아진다.
두 번째, 분산감소비율(Variance Reduction, VR)은 합성파(s)와 관측파(u)의 진폭 차이의 제곱 합으로 두 파형 사이의 유사성을 나타내는 값이다. 모든 관측소에서 각 성분에 대한 VR을 계산하고, 평균값을 얻게 되는데 VR은 식 (11)로 계산되며, 100%에 가까울수록 신뢰도가 높아진다.
| (11) |
세 번째, 조건수(Condition Number, CN)는 관측소 분포와 주파수 영역에 의해 지배받는 값이다. 이 연구에서는 11개의 관측소를 고정적으로 사용했기 때문에, 주파수 영역의 변화가 주로 CN에 영향을 미치게 된다. CN은 식 (12)로 계산된다(Sokos and Zahradnik, 2013).
| (12) |
여기서 식 (6)의 E에서 구한 최대 고유값(maxeignval)과 최소 고유값(mineigenval)의 차이가 작을수록 CN값은 작아지며, 신뢰도가 높아진다. 즉, 작은 고유값으로 인해 해가 불안정해지지 않을 때 신뢰도가 높다고 할 수 있다.
마지막으로 FMVAR (Focal Mechanism Variability Index)과 STVAR (Space-Time Variability Index)은 격자 탐색 방법으로 얻어진 진원 기구 해의 가변성을 정량화하는 수치이다. 이 연구에서는 진원 기구 해의 임계값을 (최대 상호상관 값)*0.9로 설정한다(Sokos and Zahradnik, 2013). FMVAR은 임계값 내에 속하는 해와 최대 상호상관 값을 갖는 단층면 해 사이 각도 차이의 평균을 의미하며, STVAR은 구해진 모든 진원 기구 해를 그림 3과 같이 그렸을 때, 임계값 내에 속하는 해가 차지하는 면적의 비이다.
이 연구에서는 Sokos and Zahradnik (2013)에서의 평가 기준에 근거해 SNR 10 이상, VR 90% 이상, CN 10 이하, FMVAR 30 이하, STVAR 0.3 이하를 동시에 만족하는 결과가 신뢰할 수 있다고 판단했다.
7. 주파수 영역 선택
모멘트 텐서 파형 역산에 이용될 주파수 영역을 선택하는 것은 지진의 규모와 관측소까지의 진앙 거리 등 여러 가지 요소에 좌우되기 때문에 매우 까다롭고 힘든 작업이다. 따라서 최적의 주파수 영역을 찾기 위해 일반적으로 사용되는 주파수 범위보다 더 넓은 주파수 범위(0.03 ~ 0.22 Hz) 안에서 다양한 주파수 영역을 적용해 보았고, 최적의 주파수 범위가 어디인지 알아보고자 했다.
주파수 영역을 선택하기 위해서는 사다리꼴의 꼭짓점에 해당하는 f1, f2, f3, f4를 정의해 줘야 하며, 결과에 가장 많은 영향을 미치는 주파수 영역의 시작지점인 f1과 끝 지점인 f4를 아는 것이 중요하다. f2와 f3는 각각 f1과 f4와 0.01 Hz 차이가 나도록 하였다. f1이 0.03 Hz, 0.04 Hz, 0.05 Hz 그리고 0.06 Hz일 때의 경우에 각각 f4를 0.1 Hz부터 0.01 Hz 간격으로 늘려가며, 최대 0.22 Hz까지의 모든 영역을 적용해 보았다. 그 결과, 주파수 영역과 VR의 상관관계를 그림 5과 같이 확인할 수 있었는데, f1이 0.05 ~ 0.06 Hz일 때, 그리고, f4가 0.10 ~ 0.16 Hz일 때 VR이 안정적으로 90% 이상인 값을 얻었다. 따라서 주파수 영역에 영향을 받는 신뢰성 평가요소 CN을 고려하여, 최대한 넓은 주파수 영역을 이용하고자 f1을 0.05 Hz로 선택했다. f4에 대해서는 모든 신뢰성 평가요소를 만족시키는 값은 모두 적용시켰으며, 따라서 각 모델에 대한 결과는 하나가 아닌 여러 개의 결과를 얻을 수 있다.
8. 결 과
포항지진에 대해 총 8개의 지각 속도모델을 적용해 ISOLA를 이용하여 두 종류의 모멘트 텐서 역산을 수행했고 모델과 역산 방법에 따른 결과를 표로 정리했다(표 1a-b, 표 2a-b). 표 1은 편차 응력에 의해 발생한 지진이라 가정하여 DC와 CLVD 성분만을 나타내는 편차 모멘트 텐서 역산의 결과이며, 표 2는 DC, CLVD 그리고 ISO성분까지 포함하는 전 모멘트 텐서 역산의 결과를 나타낸다. 적용된 지각속도 모델 중에서 원래의 Kim (1995) 그리고 IASP91 모델과 이 모델들에 정부조사연구단의 천부 지각모델을 포함시킨 4개의 모델을 적용했을 때 신뢰성 평가요소들을 전부 만족하는 결과가 없었기 때문에 이를 제외한 나머지 4개의 지각속도 모델에 대한 결과를 표 1, 2에 나타내었다. 이 연구에서 사용된 지각 속도모델을 두 종류로 분류하였는데, 표 1, 2의 지각 속도모델 a, b는 각각 Kim et al. (2011), Chang and Baag (2006) 지각 속도모델이며, 지각 속도모델 A, B는 모델 a, b의 상부층(약 0 ~ 7 km)에 정부조사연구단이 사용한 천부 지각모델을 결합해 만든 지각 속도모델이다.
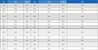
The results of deviatoric moment tensor inversions using crustal models a and A. The crustal model a is from Kim et al. (2011). The crustal model A is obtained by combining the upper part of the Korean Government Commission’s crustal model and the model a.

The results of deviatoric moment tensor inversions using crustal models b and B. The crustal model b is from Chang and Baag (2006). The crustal model B is obtained by combining the upper part of the Korean Government Commission’s crustal model and the model b.
먼저, 표 1과 2에서 포항지진 본진의 진원 깊이 결과를 보면, 3 ~ 5 km로 2 km정도의 편차가 있으며, 평균 4.04±0.54 km의 결과를 보였다. 편차 모멘트 텐서 역산의 결과만으로 평균을 구하면 4.46±0.33 km, 전 모멘트 텐서 역산의 결과만으로 평균을 구하면 3.65±0.38 km의 결과를 나타내었다. 이는 정부조사단의 결과인 4.27 km와 매우 유사함을 알 수 있다. 단층면해의 경우, 전 모멘트 텐서 역산을 한 표 2에서의 단층면해의 결과가 포항지진 정부조사연구단 요약보고서(Geological Society of Korea, 2019)에서 나와 있는 포항지진 본진의 단층면 해 결과의 주향, 경사, 미끌림각인 214°, 51°, 128°와 더 유사함을 확인할 수 있었다. DC의 함량은 표 1에서 모델 a의 평균이 41.6%로 가장 큰 값을 보였고, 모델 B에서 33.9%로 가장 작은 값을 보였다. ISO 성분이 추가된 전 모멘트 텐서 역산을 한 표 2에서는 모델 a를 제외한 나머지 3개의 모델에서 표 1에서 보다 DC 함량이 증가하였으며, 편차 모멘트 텐서 역산을 한 표 1에서의 DC 전체 평균인 38.9%보다 전 모멘트 텐서 역산을 한 표 2에서의 DC 전체평균이 40.0%로 증가했다. 표 2에서 ISO 함량은 모델 a에서 평균 16.1%로 가장 낮은 값을 보였고, 모델 b에서 평균 25.8%로 가장 높은 값을 보였다.
신뢰성 평가요소에서 SNR 같은 경우, 이 연구에 사용된 지진 자료는 잡음에 대한 영향이 굉장히 적었고, 모멘트 규모 5.4의 에너지가 비교적 큰 지진과 약 140 km 이내의 근거리에 위치한 국내 관측소 자료를 사용했기 때문에, 모든 주파수 영역에서 상당히 양호한 값을 가졌다. CN, FMVAR, STVAR 역시 표 1, 2의 모든 결과에서 양호한 값을 가졌지만, VR 값에 의해 각 모델의 결과 개수가 결정됐다. 표 1에서 모델 a의 결과는 6개이며, 평균 VR 값은 93.1%이고, 표 2에서 모델 a의 결과는 7개이며, 평균 VR 값은 92.8%로 표 1, 2에서 모델 a를 사용했을 때, 신뢰성 평가 기준을 만족하는 결과가 가장 많았으며, 평균 VR값이 가장 높았다. 표 1, 2에서 정부조사연구단의 천부 지각모델을 결합한 모델 A, B를 사용했을 때 결과의 개수가 모델 a, b에 비해 1개로 적어졌고, 평균 VR 값도 약 90.4%로 비교적 낮은 값을 보였다.
9. 결론 및 토의
이 연구에서 측정된 포항지진의 본진 진원 깊이는 3 ~ 5 km로 측정됐다. 이러한 결과는 표 1, 2에 나타낸 결과 외에도, Kim (1995)와 IASP91을 이용한 4개 모델의 결과에서도 VR이 0.6 이상이 되는 조건에서는 마찬가지로 본진 진원 깊이가 3 ~ 5 km로 일정하게 측정됨이 확인됐다. 이는 Chung et al. (2018)에서 진원 재결정 역산을 통해 6 ~ 11.5 km 구간의 깊이를 산출한 결과와 기상청에서 발간한 포항지진 분석 보고서(2018)에서 보고한, 15 km 이내 관측소를 사용했을 때 2 ~ 5 km, 50 km 이내 관측소를 사용했을 때 7 ~ 10 km로 측정된 결과와 비교했을 때, 편차가 최대 2 km 정도이고 다양한 지각속도 모델을 적용한 점까지 고려한다면, 상당히 양호한 수준의 오차임을 알 수 있다. 이는 모멘트 텐서 역산 방법이 지각속도에 대한 정보가 부족한 상황에서는, 본진의 진원 깊이를 측정하는 데에 있어서 주시 자료를 사용하는 것에 비해 상대적으로 상충효과가 적은 것을 나타내는 것으로 생각된다.
그리고 표 1, 2에서 모델 A, B의 경우 원래의 모델 a, b보다 평균 VR값이 낮고 결과 개수가 적게 나타났다. 이는 정부조사연구단에서 구한 천부지각모델이 포항 주변에 대해서는 더 정확한 모델이라고 할 수 있으나 경상분지 전체에 대한 평균적인 모델이 될 수는 없음을 나타낸다고 볼 수 있다. 기존의 모델 a, b는 경상분지 전체에 분포한 관측소에서 취득한 지진 자료를 사용한 모델이기에, 보다 평균적인 모델에 가깝다고 할 수 있으며, 따라서 원거리에 위치한 관측소에서 관측된 파형과 더 유사한 합성 파형을 도출해 내었다고 생각된다. 주파수 범위가 0.05 ~ 0.10 Hz인 경우에 모델 a와 A에 대한 파형 비교를 그림 6과 7에 나타내었다. 그림 6과 7을 비교해 볼 때 1차원 모델로는 모든 관측소에서 실제 파형과 유사한 합성 파형을 만들어 내기는 어려움을 알 수 있었다. JEJB와 GUWB 관측소의 NS 성분에서는 모델 A에서의 결과가 실제 파형과 더 유사한 파형을 만들어 내지만, YOCB 관측소에서의 EW 성분, CIGB 관측소에서의 수직 성분, GDDB 관측소의 NS 성분 등에서는 모델 a에서의 결과가 더 유사한 파형을 만들어 내기 때문이다. 그래도 앞서 설명한 바와 같이 모델 a가 2.4% 더 높은 VR을 보이기 때문에 경상 분지 평균 모델을 사용하는 것이 정부조사연구단 모델보다 더 좋은 결과를 얻게 하는 것을 볼 수 있었다.

Comparison of observed and synthetic waveforms of deviatoric moment tensor inversion for all stations with a frequency range of 0.05 ~ 0.10 Hz using crustal model a. Values in blue on the right-hand side are VR values.

Comparison of observed and synthetic waveforms of deviatoric moment tensor inversion for all stations with a frequency range of 0.05 ~ 0.10 Hz using crustal model A. Values in blue on the right-hand side are VR values.
다음으로 non-DC 성분을 이용하여 포항지진 본진에 유체에 대한 영향이 얼마나 큰지 알기 위해서 전 모멘트 텐서 역산을 수행해 CLVD와 ISO 성분 함량을 측정했다(표 2). 모델에 따라 ISO 성분은 15.1 ~ 28.8% 정도로 측정되었다. 하지만, 편차 모멘트 텐서 역산한 결과(표 1)와 비교했을 때, VR값이 거의 비슷하게 측정되었고, 이는 전 모멘트 텐서 역산에서 사용된 모델 파라미터의 개수가 늘어났기 때문에 합성 파형이 관측파와 더 잘 맞을 것이라는 기대를 만족시키지 못한 결과였기 때문에 표 2의 결과를 신뢰하기는 어렵다고 생각된다. 그러나 표 2에서 나온 결과가 정부조사연구단에서 여진들의 진원 분포를 통해 파악한 단층면의 주향과 경사인 214°, 43°와 더 유사한 점, 그리고 ISO 성분을 추가할 때 관측소 JEJB와 GDDB의 NS 성분이 크게 개선되는 점 등을 고려할 때(그림 8; 0.05 ~ 0.10 Hz의 주파수 범위) 단층 활동시 유체에 의해 부피 변화가 있었을 가능성도 후속 연구를 통해 고려할 필요가 있을 것으로 생각된다. Grigoli et al. (2018)의 전 모멘트 텐서 역산 결과에서도 ISO 성분이 13% 있는 것으로 계산되었다.

Comparison of observed and synthetic waveforms of full moment tensor inversion for all stations with a frequency range of 0.05 ~ 0.10 Hz using crustal model a. Values in blue on the right-hand side are VR values.
CLVD 성분도 모델에 따라 편차 모멘트 텐서 역산을 수행했을 경우에는 56 ~ 66%로 상당히 높게 측정되었고, 전 모멘트 텐서 역산을 수행했을 경우에도 29 ~ 46%로 높게 측정되었다. CLVD 성분은 유체의 이동에 의해서도 발생하지만 거의 동시에 비슷한 지역에서 발생한 다른 형태의 DC가 겹치게 될 때에도 발생할 수 있다. Grigoli et al. (2018)은 포항 지진의 높은 CLVD 성분을 복잡한 단층대에 기인한 것으로 판단하였다. Wang et al. (2018)은 캐나다 서부에서 발생한 자연 지진과 유발 지진의 CLVD 성분을 측정, 비교함으로써 CLVD 성분의 함량으로는 자연 지진과 유발 지진을 구분할 수 없음을 보여주었다. 따라서 현재로서는 non-DC 성분을 통해서 유발 지진의 여부를 판단할 수는 없을 것으로 생각된다.
최종적으로 표 1에서 4개의 지각모델과 다양한 주파수 영역에서의 결과를 토대로 평균과 표준편차를 구해볼 때 포항지진 본진의 진원 깊이는 4.46±0.33 km인 것으로 생각된다. 포항지진 본진의 위치와 포항 지열발전소의 위치가 약 500 m 정도로 매우 가까우며(그림 9), PX1, PX2 지열정의 깊이가 4.215 km와 4.340 km로 이 연구에서 얻어진 본진의 진원 깊이와 상당히 비슷한 점으로 보아 포항 지열발전소에서의 물 주입이 포항지진이 발생한 단층에 상당 부분 영향을 준 것으로 보인다. 지열발전소에서의 최종 물 주입과 포항지진의 발생 사이의 2달 정도의 시간 차이가 존재하지만(Kim et al., 2018), Bao and Eaton (2016)에 의하면 유발 지진이 관정의 깊이에서부터 1 km 이상 떨어져 발생할 수도 있고, 시간적으로 지연되어 발생할 수도 있기 때문에 포항 지진은 지열발전소의 활동에 의한 유발(induced) 혹은 촉발(triggered) 지진일 가능성이 있다고 할 수 있다.
Acknowledgments
이 논문은 행정안전부장관의 지진방재분야 전문인력 양성사업으로 지원되었으며 2019년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No.2019R1A6A1A03033167).
References
- Aki, K. and Richards, P.G., 2002, Quantitative Seismology. University Science Books, Sausalito, 704 p.
-
Bao, X. and Eaton, D.W., 2016, Fault activation by hydraulic fracturing in western Canada. Science, 354, 1406-1409.
[https://doi.org/10.1126/science.aag2583]

-
Chang, S.-J. and Baag, C.-E., 2006, Crustal structure in southern Korea from joint analysis of regional broadband waveforms and travel times. Bulletin of the Seismological Society of America, 96, 856-870.
[https://doi.org/10.1785/0120040165]

- Chung, T.W., Lee, Y., Iqbal, M.Z. and Jeong, J., 2018, A study of hypocentral depth of Pohang earthquake. Geophysics and Geophysical Exploration, 21, 125-131 (in Korean with English abstract).
-
Geological Society of Korea, 2019, Summary report of the Korean Government Commission on relations between the 2017 Pohang earhquake and EGS project. The Geological Society of Korea,
[https://doi.org/10.22719/KETEP-20183010111860]

-
Grigoli, F., Cesca, S., Rinaldi, A.P., Manconi, A., López-Comino, J.A., Clinton, J.F., Westaway, R., Cauzzi, C., Dahm, T. and Wiemer, S., 2018, The November 2017 Mw 5.5 Pohang earthquake: A possible case of induced seismicity in South Korea. Science, 360, 1003-1006.
[https://doi.org/10.1126/science.aat2010]

-
Kennett, B.L.N. and Engdahl, E.R., 1991, Traveltimes for galobal earthquake location and phase identification. Geophysical Journal International, 105, 429-465.
[https://doi.org/10.1111/j.1365-246X.1991.tb06724.x]

- KIGAM, 2016, http://quake.kigam.re.kr/earthquake/eqViewUser.do?menu_nix=3Wlr1F77&edomweivgp=M&eq_no=1347, (July 28, 2019).
-
Kim, K.-H., Ree, J.-H., Kim, Y.H., Kim, S., Kang, S.Y. and Seo, W., 2018, Assessing whether the 2017 MW 5.4 Pohang eartquake in South Korea was an induced event. Science, 1009, 1007-1009.
[https://doi.org/10.1126/science.aat6081]

-
Kim, S., Rhie, J. and Kim, G., 2011, Forward waveform modelling procedure for 1-D crustal velocity structure and its application to the southern Korean Peninsula. Geophysical Journal International, 185, 453-468.
[https://doi.org/10.1111/j.1365-246X.2011.04949.x]

- Kim, S.K., 1995, A Study on the Crustal Structure of the Korean Peninsular. Journal of the Geological Society of Korea, 31, 393-403 (in Korean with English abstract).
- Klein, F.W., 2007, User's guide to HYPOINVERSE‐2000, a Fortran program to solve for earthquake locations and magnitudes. U.S. Geological Survey, Open File Report, 02‐171.
- Korea Meteorological Administration (KMA), 2016, http://web.kma.go.kr/notify/press/kma_list.jsp?bid=press&mode=view&num=1193259, (July 28, 2019).
- Korea Meteorological Administration (KMA), 2018, Pohang Earthquake Analysis Report. https://www.weather.go.kr/weather/eartquake_volcano/major_pohang.jsp, (July 28, 2019).
-
Lee, H. and Sheen, D.-H., 2015, A study on determination of orientation of borehole seismometer. Journal of the Geological Society of Korea, 51, 93-103 (in Korean with English abstract).
[https://doi.org/10.14770/jgsk.2015.51.1.93]

- Ministry of the Interior and Safety, 2018, 2017 Statisical Yearbook of Natural Disaster. https://www.mois.go.kr/cmm/fms/FileDown.do?atchFileId=FILE_00078263Dw0cpT-&fileSn=2, (July 28, 2019).
-
Sokos, E.N. and Zahradnik, J., 2008, ISOLA a Fortran code and a Matlab GUI to perform multiple-point source inversion of seismic data. Computers and Geosciences, 34, 967-977.
[https://doi.org/10.1016/j.cageo.2007.07.005]

-
Sokos, E.N. and Zahradnik, J., 2013, Evaluating Centroid-Moment-Tensor Uncertainty in the New Version of ISOLA Software. Seismological Research Letters, 84, 656-665.
[https://doi.org/10.1785/0220130002]

-
Waldhauser, F. and Ellsworth, W.L., 2000, A double-difference earthquake location algorithm: Method and application to the northern Hayward fault, California. Bulletin of the Seismological Society of America, 90, 1353-1368.
[https://doi.org/10.1785/0120000006]

-
Wang, R., Gu, Y.J., Schultz, R. and Chen, Y., 2018, Faults and non-double-couple components for induced earthquakes. Geophysical Research Letters, 45, 8966-8975.
[https://doi.org/10.1029/2018GL079027]









