동굴생성물 연대 모델 설정을 위한 통계 알고리즘의 비교
초록
합리적인 동굴생성물의 연대모델 정립을 위해 각 통계 알고리즘의 개발 철학과 구동특성을 이해하는 것이 매우 중요하다. 이 연구에서는 동굴생성물의 연대모델을 효율적으로 작성하기 위해 연구자가 이해해야 할 통계 알고리즘의 특성을 제시하고자 한다. 이를 위해 성장률 특성이 뚜렷하게 구별되는 국내 석순 시료 5점을 선별하여 현재까지 동굴생성물 고기후 연구에 가장 널리 활용되고 있는 3종의 통계 알고리즘(StalAge, COPRA, MOD-AGE)을 통해 연대모델을 작성한 후 그 결과를 비교·분석했다. 연구 결과, 성장률이 비교적 일률적인 백룡동굴의 석순(BN-1)과 석순이동굴의 석순(SSN1)의 경우, COPRA와 MOD-AGE의 작성결과에서 연대자료 입력치를 가장 잘 반영하는 것으로 나타났다. 이와는 달리, 1회 이상의 유의미한 휴지기를 포함하고 있는 대야굴, 삼각산수직굴, 에덴동굴 석순(DY-1, SGS1, ED-1)의 예에서는 입력치 및 성장특성 반영정도를 고려하여 COPRA, MOD-AGE, StalAge 중 적합한 알고리즘 선택이 필요하다. 한편, 통계알고리즘 별 개발철학과 구동특성에 기반하여 COPRA는 비교적 정밀하게 측정된 연대자료에 대하여 높은 입력치 반영 정도를 나타내는 반면, 통계 알고리즘의 필요성이 더욱 높아지는 다소 큰 오차의 연대자료가 포함될 경우 최종모델을 작성하지 못하는 한계를 보인다. 이와는 반대로 StalAge는 객관적 연대모델 작성을 최우선시하기 때문에 오차가 큰 연대자료를 통해 최종모델을 작성하는데 탁월하고 휴지기 표현에 가장 우수한 반면, 상대적으로 낮은 입력치 반영 정도를 나타내는 단점을 보인다. 이번 연구는 현재 특별한 기준 없이 적용되는 통계적 연대모델 활용사례에 대한 문제점을 환기하며, 아울러 동굴생성물 통계 연대모델 작성 이전 최적의 결과 구현을 위한 통일된 대안의 필요성을 강조한다. 이 연구의 결과는 연대모델 작성이 이루어지는 대부분의 고기후 기록물(paleoclimatic archives)에 동일하게 적용될 수 있다.
Abstract
It is very important to understand the philosophy and operation properties of statistical algorithms for constructing realistic age-depth models of speleothems. This study presents the characteristics of statistical algorithms designed for speleothems. We have selected previously published five Korean stalagmites with distinct characteristics of the changes in growth rates. Then, the age-depth models of these stalagmites were constructed using 3 statistical algorithms (StalAge, COPRA, MOD-AGE) which have been widely applied to the recent cave records. The age-depth models resulted from COPRA and MOD-AGE show the lowest deviations from median 230Th ages when the stalagmite samples have relatively constant growth rates (the cases of BN-1 and SSN1). In contrast, for the stalagmites (DY-1, SGS1 and ED-1) including significant hiatuses with large time gaps, the most convinced model can be selected depending on both 230Th ages and petrographic data. COPRA simulates age-depth models with good agreements to 230Th ages, but it is sometimes impossible to construct final models when the dataset includes 230Th ages with large errors and/or inversions in the stratigraphic order. StalAge could be preferred to simulate the age-depth relationships in the cases of the dataset with large errors or age inversions but this provides the largest deviations from 230Th ages. The results of this study emphasize the needs of criteria to construct the most reliable age-depth model for speleothems using the statistical algorithms. Our results can be equally applied to various paleoclimatic archives (e.g., terrestrial sediments) that require similar age-depth models.
Keywords:
Speleothem, Statistical age-depth models, StalAge, COPRA, MOD-AG키워드:
동굴생성물, 통계적 연대모델, StalAge, COPRA, MOD-AGE1. 서 론
연대측정은 고기후 연구에서 가장 근간이 되는 분석 과정 중 하나이다. 동굴생성물의 우라늄 계열 연대측정의 경우 통상적으로 측정연대 값의 약 5% 이내의 오차(Cheng et al., 2013)를 보여 다양한 고기후 기록물들(paleoclimatic archives)에 적용되는 여러 연대측정법 중 가장 정밀한 수준의 연대 자료 산출이 가능하다(McDermott, 2004; Dorale et al., 2007; Hercman and Pawlak, 2012). 그러나 이러한 동굴생성물 연대측정을 비롯한 모든 연대측정 자료들은 자체적으로 불연속적인 특성을 내포하며 다량의 분석 시간과 비용이 소요된다. 이러한 문제점을 최소화하기 위해 많은 연구자들이 상대적으로 적은 양의 연대 자료를 사용하여 연속적이고도 객관적인 연대 정보를 얻을 수 있는 연대 모델을 설정한다. 연대 모델 중 가장 기본적인 기법으로 선형 보간법(linear interpolation)이 있다. 그러나 선형 보간법은 항상 임의의 연대측정 위치를 기준으로 성장률이 급격하게 변한다는 점에서 비현실적인 모델을 구현하며, 때때로 연대 자료의 오차 범위가 겹치거나 역전 값을 포함하는 경우 자연계에서 발생할 수 없는 음의 성장률을 표현(Scholz and Hoffmann, 2011)하여 연구자의 주관적인 해석에 의해서 연대 모델 작성에 사용한 입력치에 대한 임의의 조절 또는 제거가 필요할 수 있다. 이때, 통계적 접근은 연구자의 주관적인 해석을 배제시킨 모델 제시를 통해 연대 모델에 객관성을 부여하며 선형 보간법에 의한 문제점을 보완할 수 있다. 이에 따라 방사성 탄소 연대측정과 관련하여 퇴적물의 연대 모델을 작성하는 통계적 기법이 여러 차례 제시되어 왔으며(Blaauw and Christen, 2005; Heegaard et al., 2005; Blaauw, 2010; Blaauw and Christen, 2011), 이후 동굴생성물 연구에 대한 관심이 지속적으로 높아지면서 동굴생성물 연대측정값을 중심으로 모델을 작성하는 통계적 알고리즘이 소개되었다. 대표적인 동굴생성물 통계적 연대 모델 작성 알고리즘에는 StalAge (Scholz and Hoffmann, 2011), COPRA (Breitenbach et al., 2012), MOD-AGE (Hercman and Pawlak, 2012)가 있으며, 현재까지 많은 연구자들에 의해 널리 사용되어지고 있다(Liu et al., 2016; Arienzo et al., 2017; Mehterian et al., 2017; Mori et al., 2018).
통계적 기법을 활용한 연대 모델 작성은 선형 보간법의 단점을 보완하여 객관성을 유지하면서 더욱 현실적인 연대 모델을 작성할 수 있다. 그러나 서로 다른 개발 철학과 구동 특성으로 인해 동일 연대 자료 사용에도 불구하고 선택한 통계 알고리즘에 따라 서로 다른 결과를 작성한다는 문제점을 내포한다. 따라서 동굴생성물 연대 모델 작성을 위한 통계 알고리즘 사용에는 이들 속성에 대한 면밀한 이해가 전제되어야 하며, 더 나아가 연대 자료와 각 동굴생성물 시료 별 특성을 반영하는 통계적 알고리즘의 적용기준 마련이 필요하다. 동굴생성물 연대자료를 활용한 통계적 연대모델 비교는 Scholz et al. (2012)에 의해 제한적으로 진행되었던 바 있지만 StalAge를 제외하면 주로 14C 연대자료를 대상으로 육상 퇴적물의 연대모델 작성 통계기법이 사용되었다. 이번 연구에서는 현재 동굴생성물 고기후 연구에서 널리 사용되고 있는 세 가지 통계 알고리즘을 사용하여 기존 발표된 국내 석순 중 성장특성이 뚜렷하게 구별되는 5점에 대한 연대 모델을 작성하고 그 결과를 상호 비교하였다. 최종적으로 세 가지 알고리즘에 의해 작성된 연대 모델에서 나타나는 장점 및 문제점을 파악하고, 연구자가 이해해야 할 동굴생성물 특화 통계 알고리즘의 특성을 제시하고자 한다.
2. 연구방법
2.1 동굴생성물 시료 선별
동굴생성물 성장 특성에 따른 통계 알고리즘 별 연대 모델 작성 결과 비교를 위해 기존 발표된 국내 석회동굴 석순 자료 5점을 선별하였다(표 1). 선별된 석순시료는 기존 연구(Jo et al., 2006, 2011, 2014, 2017)의 230Th 연대측정 자료 및 주요 조직분석 결과에 근거하여 1) 유의미한 휴지기 없이 비교적 일률적인 성장률로 성장한 백룡동굴 석순(BN-1), 석순이동굴 석순(SSN1)과 2) 주요 휴지기를 포함하는 대야굴 석순(DY-1), 삼각산수직굴 석순(SGS1), 에덴동굴 석순(ED-1)으로 나눌 수 있다.
2.2 연대 모델 작성에 사용한 통계 알고리즘
유의미한 휴지기 존재 유무에 따른 성장 특성이 통계 연대 모델에 의해 반영되는 정도를 평가하기 위하여 현재 동굴생성물 고기후 연구에서 널리 사용되고 있는 세 가지 통계적 연대 모델 알고리즘 StalAge, COPRA, MOD-AGE를 사용하였다(표 2). 이들 통계 알고리즘에 대한 상세한 설명은 각각 Scholz and Hoffmann (2011), Breitenbach et al. (2012), Hercman and Pawlak (2012)에 기술되어 있다. 각 알고리즘 별 개발 철학 및 보간법에 대해 간략히 소개하면 다음과 같다.
이번 연구에서 사용한 세 가지 통계 알고리즘은 모두 오픈소스 프로그램을 기반으로 하며, 오차 범위 내 무작위 값(난수)을 이용하여 반복적인 계산을 진행하는 몬테카를로 시뮬레이션(MC-simulation)에 의해 연대 모델 및 95% 신뢰구간을 작성한다. StalAge는 최소 3점 간 직선 관계를 기반으로 오차 범위 내 몬테카를로 시뮬레이션에 의한 반복 계산으로 연대 모델과 신뢰구간을 작성한다(그림 1a). 또한 여러 변수의 조절이 불가능하여 연구자의 해석 및 임의의 조절이 최소화된 객관성 높은 결과를 도출할 수 있다. COPRA는 각 연대측정값의 오차 범위 내 정규분포를 계산하여 반복적인 몬테카를로 시뮬레이션 실행을 통해 연대 모델과 신뢰구간을 얻어낸다(그림 1b). 뿐만 아니라 연간 성장띠(annual growth bands) 정보를 추가할 수 있어 더 정밀한 연대 모델 작성이 가능하다. MOD-AGE는 동굴생성물의 연속적인 성장을 가정하는 연대 모델을 기반으로 몬테카를로 시뮬레이션에 의해 연대측정값과 깊이 값의 오차 범위 내에서 타원형의 무작위 범위를 결정한 후 LOESS (locally weighted scatterplot smoothing) 보간법을 사용하여 연대 모델을 작성하며(그림 1c), SPAN factor에 의해 평활화(smoothing) 정도를 결정한다(Cleveland and Devlin, 1988).
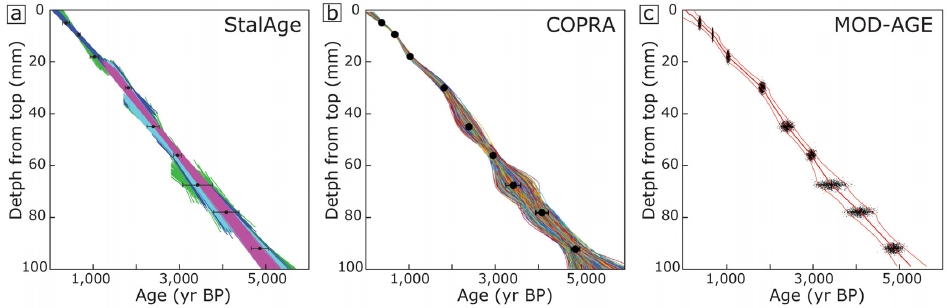
Comparison of 3 statistical algorithms for speleothems using BN-1 age data. (a) StalAge conducts Monte-Carlo simulation within the error range based on linear interpolation between at least 3 points. (b) COPRA has constructed Monte-Carlo simulations of the entire section. The error range is short because 1/2 error is input by mechanism. (c) MOD-AGE has established the elliptical random range to construct age-depth model.
StalAge는 더 객관적인 연대 모델 작성을 위하여 사용자에 의한 조절이 전면적으로 제한되지만 COPRA와 MOD-AGE는 일부 선택이 가능하다. 이번 연구에서는 COPRA 연대 모델 보간법(1차, 3차, 스플라인 함수) 중 이 연구를 위해 선택된 석순 5점에 대한 연대 모델 계산 실행이 가능한 3차 함수(cubic function)를 선택하였으며, 몬테카를로 시뮬레이션 횟수는 기본 설정 값인 2,000회로 고정하였다. MOD-AGE의 연대 모델 보간법 적용의 경우, 선형 보간법과 LOESS 중 해당 알고리즘 특성을 더 부각시킬 수 있는 LOESS 보간법을 선택하였으며, 연대 모델의 평활화 정도를 결정하는 SPAN factor는 프로그램 자체적으로 계산해 주는 자동기능(Automatic function)을 선택하고 몬테카를로 시뮬레이션은 1,000회로 고정하였다.
2.3 통계적 알고리즘 평가 기준
동굴생성물 통계적 연대 모델 작성에서 기초가 되는 유일한 자료는 우라늄 계열 연대측정 자료와 이에 대한 오차범위 자료이다. 정밀한 연대측정을 전제하에, 오차 범위 내에서 연대자료의 중앙값(median value)을 최대한 반영하는 연대 모델이 가장 신뢰도가 높은 합리적인 결과일 수 있다(Telford et al., 2004; Trachsel and Telford, 2017). 그러나 통계 알고리즘에 의해 작성된 연대 모델은 같은 입력치를 사용하더라도 데이터의 질 또는 알고리즘의 개발 철학, 구동 특성에 따라서 연대자료의 중앙값과 편차가 발생하거나 심지어 오차 범위를 벗어남으로써 입력치를 반영하지 못하는 연대 모델을 작성할 수 있다. 따라서 통계 알고리즘 별 각 동굴생성물의 연대 자료 반영 정도를 평가하기 위해 알고리즘에 의해 계산된 연대와 연대 자료의 중앙값의 편차를 대비하였다. 추가적으로 휴지기를 포함하는 석순에 대해서 휴지기 재현 정도를 평가하였다. 이는 조직 관찰에 의해 확인된 휴지기 구간이 연대 모델 내에서도 동일하게 재현되는지 확인하기 위해 성장률을 기준으로 비교하였다.
3. 동굴생성물 성장 특성 별 통계적 연대 모델 비교결과
3.1 일률적인 성장률의 석순
SSN1 (Jo et al., 2014)은 전체적으로 흰색 내지 매우 옅은 황색의 석순으로 육안 상 성장선이 매우 잘 관찰되며, 공극이나 변질 또는 휴지기로 추정되는 조직은 나타나지 않는다(그림 2a). 연대측정 결과 5점의 연대 자료가 3,414±149년 전부터 1,325±204년 전 이내에서 인접한 연대 자료 간 오차 범위가 겹치며 나타난다(그림 2b). SSN1 석순의 StalAge 연대 모델은 오차 범위 내에서 성장률 변화가 거의 없는 최상부와 최하부의 두 연대측정값을 연결한 직선 모델과 거의 유사하게 나타난다(그림 2c). 따라서 연대 자료의 중앙값(입력치)을 반영하기보다 성장률 변화가 거의 없이 일정한 연대 모델을 작성함으로써 연대 자료와 연대 모델에 의해 계산된 연대의 편차가 약 10~171년으로 세 연대 모델 중 가장 큰 차이를 보인다. 반면 MOD-AGE는 상대적으로 연대 자료를 반영하는 모델을 작성함으로써 선형 보간법과 거의 유사한 결과를 보인다(그림 2e). 따라서 연대측정값과 연대 모델에서 계산한 연대 값의 편차가 2 ~ 21년으로 상대적으로 가장 작게 나타난다. 그러나 일부 연대측정값 부근에서 성장률이 비정상적으로 급격하게 증가하는 특징이 나타난다(그림 2a, 2e). 이러한 특징은 연대 자료와는 무관한 명백한 알고리즘 오류(algorithm artifacts)로 차후 수정이 필요하다. COPRA는 StalAge에 비해 연대측정 값과의 편차가 작고, MOD-AGE에 비해 급격한 성장률 변화 없이 부드럽게 연결되는 연대 모델을 작성한다(그림 2d).
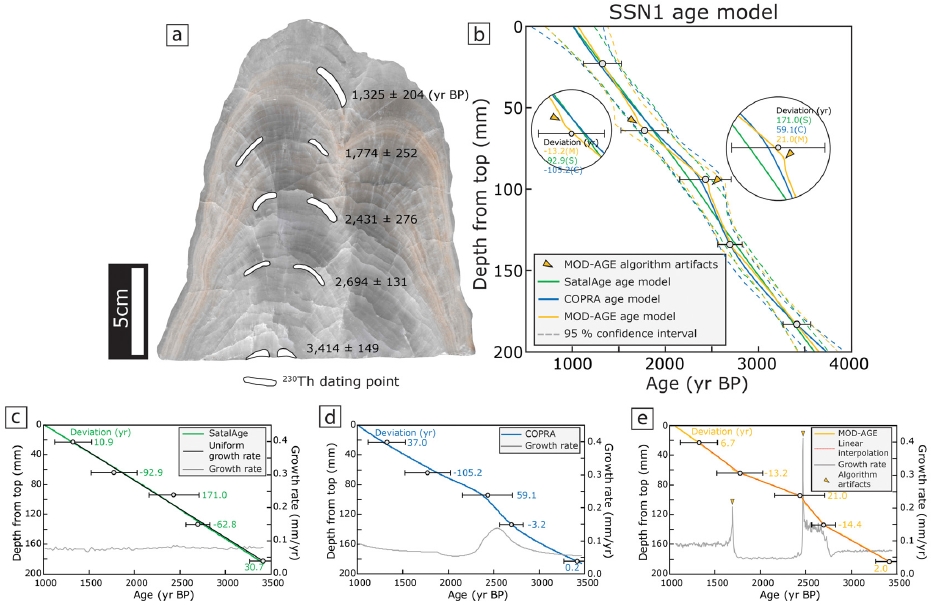
(a) A rock slab of stalagmite SSN1 showing sub-sampling points for 230Th dating. (b) SSN1 age-depth models using 3 statistical algorithms. The circle shows the algorithm artifacts (yellow arrows) produced by MOD-AGE. (c) StalAge age-depth model. (d) COPRA age-depth model. (e) MOD-AGE age-depth model. The deviation is the difference between the median values of the dating results and the yielded ages by algorithms.
BN-1 (Jo et al., 2017)은 4,863±201년 전부터 372±32년 전 사이에 성장한 석순으로 회색 내지 흰색을 띠며, 중하부에 쇄설성 물질을 포함한 성장선이 관찰(그림 3a) 된다. 또한 77.59~79.0 mm와 82.5 mm 지점에서 뚜렷한 주황색, 검은색 성장선이 관찰되지만 연대 자료와 대비한 결과 유의미한 휴지기가 아니라고 판단하였다. 세 가지 통계적 연대 모델 비교 결과 StalAge는 전반적으로 성장률 변화가 거의 없는 연대 모델을 작성한다(그림 3c). 인접한 연대 자료 간 오차 범위가 중첩되는 하부에서는 SSN1 연대 모델과 같은 특징을 보이지만, 연대 자료 간 오차 범위가 겹치지 않는 상부에서는 5 mm, 18 mm 지점의 연대 자료와 같이 오차 범위 내에서 벗어난 연대 모델을 작성(그림 3b) 한다. 따라서 StalAge에 의해 계산된 연대와 중앙값의 편차가 약 8~94년으로 세 알고리즘 중 가장 큰 차이를 보인다. 반면 COPRA와 MOD-AGE 연대 모델은 각각 20년, 10년 내외의 편차를 보이며 상대적으로 연대 자료를 반영하는 모델을 작성한다(그림 3d, 3e). 또한 성장률 변화 측면에서 COPRA는 점진적인 성장률 변화를 보이지만 MOD-AGE는 연대측정값을 지나면서 급격한 성장률 변화를 나타내는 선형 보간법에 가까운 특징을 나타내는 것으로 전반적으로 BN-1의 세 통계적 연대 모델이 모두 SSN1 연대 모델과 비슷한 특성을 보인다.
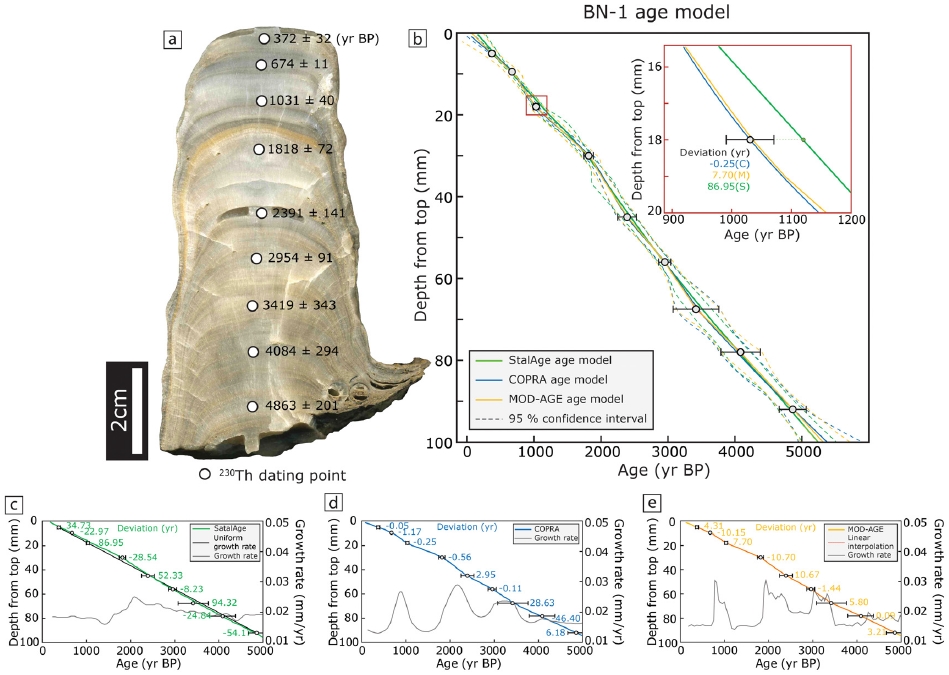
(a) A rock slab of stalagmite BN-1 showing sub-sampling points for 230Th dating. (b) BN-1 age-depth model constructed using 3 statistical algorithms. The red box shows that age-depth model deviated from age data. S, C, M means deviation from each StalAge, COPRA and MOD-AGE age-depth. (c) StalAge age-depth model and uniform growth rate line. (d) COPRA age-depth model. (e) MOD-AGE and linear interpolation age-depth model. The deviation is the difference between the median values of the dating results and the yielded ages by algorithms.
3.2 휴지기를 포함하는 석순
DY-1 (Jo et al., 2011)은 투명한 옅은 노란색을 띠는 석순으로, 상부로부터 약 28 mm 지점에서 5 mm 정도 두께의 일반적인 석순 성장 조직과 다른 불투명한 흰색 영역이 관찰된다. 이 조직을 기준으로 연대측정 결과 약 10만 년의 시간 간격이 나타난다(그림 4a, 4b). 따라서 이 구간을 DY-1 석순의 주요 휴지기로 판단하고 세 통계 연대 모델을 상호 비교하였다. 그 결과 StalAge는 휴지기 기준 상부 연대 자료(10, 15 mm 지점)로부터 벗어나는 연대 모델을 작성하여 약 4,000년 늦은 성장을 나타낸다(그림 4c). 휴지기 기준 하부 6지점의 연대 자료는 계산된 연대모델에 의하여 약 2,000~4,000년 먼저 성장하는 결과를 보인다(그림 4d). 뿐만 아니라 연대 자료와 비교하여 성장 중단이 5,000년 정도 빠르게 발생하고 4,000년 정도 늦게 종료되어 휴지기 시기에도 큰 차이가 나타나며, 휴지기 전후에서는 알고리즘 오류도 발생한다. 한편 COPRA와 MOD-AGE는 휴지기 전후 연대 자료를 잘 반영하는 연대 모델을 작성한다(그림 4c, 4d). 특히 휴지기 상부 연대 자료에 대해서 COPRA는 2년 이내, MOD-AGE는 20년 이내의 편차를 나타내고, 휴지기 하부 연대 자료에 대해서는 COPRA는 700년 이내, MOD-AGE는 800년 내외의 편차를 나타냄으로써 StalAge에 비해서 상대적으로 연대 자료를 반영하는 결과를 보인다. 그러나 휴지기 전후 연대 자료에 대해서 COPRA는 10년 이내의 편차를 보이는 반면 MOD-AGE는 20,000년 내외의 편차와 함께 알고리즘 오류도 발생된다. 정리하자면 StalAge는 모든 연대 자료를 반영하지 못하는 결과를 작성하였으며, MOD-AGE는 휴지기 구간 설정에 있어 연대 자료를 반영하지 못하였고, COPRA는 세 연대 모델 중 가장 연대 자료를 잘 반영하는 모델을 작성하였다. 한편 휴지기 재현 정도를 비교하기 위해 성장률을 계산한 결과 휴지기 구간의 성장률에 대하여 StalAge 0.019 µm/yr, COPRA 0.020 µm/yr, MOD-AGE 0.038 µm/yr로 StalAge가 가장 느린 성장률로 휴지기 구간을 표현하였으며 MOD-AGE는 약 2배 빠르게 표현된다.
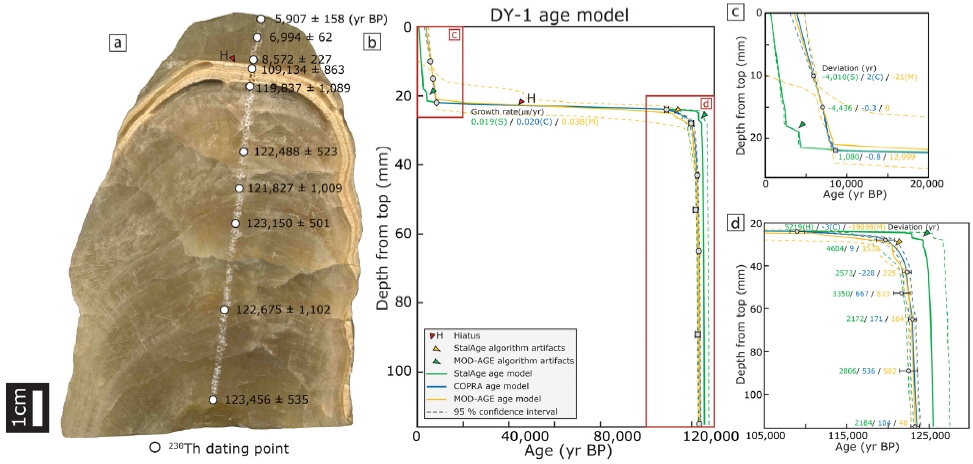
(a) A rock slab of stalagmite DY-1 showing sub-sampling points for 230Th dating and H indicates hiatus, which means interruption to the growth of speleothems. (b) DY-1 age-depth model constructed using 3 statistical algorithms and the arrow indicates calculated the algorithm artifacts. H indicates hiatus and the growth rate was calculated by each statistical algorithm. The yellow and green arrows show the algorithm artifacts produced by each MOD-AGE and StalAge. (c) Upper part and (d) lower part of age-depth models. The deviation is the difference between the median values of the dating results and the yielded ages by algorithms. S, C, M means deviation from each StalAge, COPRA and MOD-AGE age-depth.
SGS1 (Jo et al., 2014)은 연대측정 결과에 의해 128,443±1,823년 전부터 102,221±1,898년 전까지 성장한 석순으로 옅은 갈색을 띠는 석순으로 전체적으로 갈색 또는 붉은 색 계열의 성장선이 뚜렷하게 나타난다. 상부로부터 5 mm 지점에서 약 3~5 mm 구과상(spherulitic) 내지 가지상(dendritic)의 동굴산호(그림 5a)가 나타난다. 동굴산호는 기존 연구에 의하여 강수량이 매우 적고 건조한 기후 또는 지하수 순환이 원활하지 않은 조건에서 성장하는 동굴생성물로 알려져 있다(Jo et al., 2006; Caddeo et al., 2015). 또한 동굴산호의 성장 전후의 연대측정 결과 약 8,000년의 시간적 간격이 나타난다. 따라서 이 구간을 SGS1 석순 성장의 주요 휴지기로 판단하고 세 통계적 연대 모델 간 비교를 진행하였다(그림 5a, 5b). StalAge는 최상부(4.5 mm)와 최하부(133 mm) 연대 자료를 반영하지 않는 모델을 작성함으로써 휴지기를 재현하지 못한다(그림 5c). COPRA는 최상부, 최하부의 연대측정값을 선택하는 연대 모델을 작성하지만 최상부 연대 자료와 약 1,386년, 8 mm 지점의 연대 자료와 약 1,871년의 편차가 난다(그림 5d). MOD-AGE는 SSN1, BN-1 석순 결과와 같이 선형 보간법에 가까운 연대 모델을 작성하며, 8 mm, 50 mm, 71 mm 부근에서 알고리즘 오류가 발생한다. 휴지기 구간에 대하여 COPRA는 0.669 µm/yr, MOD-AGE 0.524 µm/yr의 성장률로 표현하며(그림 5d, 5e) MOD-AGE가 더 느린 성장률로 휴지기 구간을 나타낸다.
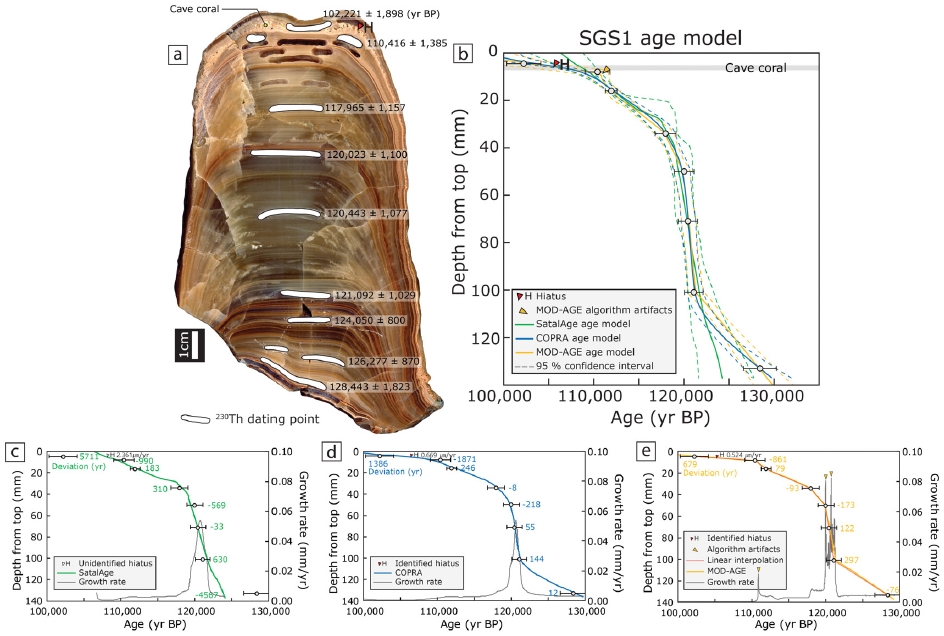
(a) A rock slab of stalagmite SGS1 showing sub-sampling points for 230Th dating H indicates hiatus by cave coral. Also shown are the cave coral growth. (b) SGS1 age-depth model constructed using 3 statistical algorithms. Gary bar indicates cave coral part and H indicates hiatus. The yellow arrows show the algorithm artifacts produced by MOD-AGE. (c) StalAge age-depth model. (d) COPRA age-depth model. (e) MOD-AGE and linear interpolation age-depth model. The deviation is the difference between the median values of the dating results and the yielded ages by algorithms. Also, StalAge is not identified hiatus(white arrow), COPRA and MOD-AGE are identified hiatus(red arrow) in age models.
ED-1 (Jo et al., 2006, 2014)은 540,022±20,050년 전부터 96,309±1,039년 전까지 성장한 석순으로 조직적 특성과의 대비 결과 약 7번의 휴지기(그림 6a)가 있었던 것으로 확인된다(Jo et al., 2014). 특히 57~93 mm 구간에서는 석순 성장이 멈추고 동굴산호가 성장한 것이 확인되는데 이 구간은 연대 자료 결과에서도 약 94,000년의 시간 간격이 나타난다. ED-1은 석순 내 여러 번의 휴지기를 포함하며 DY-1, SGS1 연대 자료와는 다르게 역전 값 및 넓은 오차 범위를 갖는 이상치(outlier)를 다수 포함한다. 통계 연대 모델 작성에 있어 StalAge와 MOD-AGE는 38점의 모든 연대 자료를 사용했지만(그림 6b, 6d), COPRA는 이상치를 포함한 연대 자료 입력 시 연대 모델 계산이 완료되지 못하는 한계를 보였다. 따라서 COPRA의 경우 주관적 자료 적격성 판단이 필요하며, 이 연구에서는 역전 연대 및 넓은 오차 범위를 갖는 연대 자료 7점을 제외하고 상부(0~93 mm)와 하부(93~188 mm)를 나누어 연대 모델을 작성하였다(그림 6c). 7번의 휴지기 중 연대측정 자료로 해상이 되지 않는 짧은 구간에서 나타나는 두 번의 휴지기(H4, H7)를 제외한 다섯 번의 휴지기는 세 통계 알고리즘에 의해 각각 다른 연대 모델로 표현된다. 세 연대 모델 비교 결과 StalAge는 COPRA와 MOD-AGE에 비해 더 느린 성장률로써 다섯 번의 휴지기를 표현한다. 특히 첫 번째 세 번째 구간의 휴지기는 각각 0.028 µm/yr, 0.037 µm/yr의 성장률로 나타나는데, 이는 1,000년에 0.5 mm 미만의 성장을 한 것을 의미하며 성장 중단에 가까운 성장률로 표현된다. 두 번째 휴지기 구간에서는 COPRA와 MOD-AGE 연대 모델 결과 136 mm 지점의 역전된 연대 자료를 제외한 연대 모델을 작성한다. 이는 StalAge는 연대 모델에서도 제외된 결과를 보이지만 역전된 연대 자료를 반영하여 신뢰 구간을 넓게 표현함으로써 휴지기의 가능성을 나타낸다(그림 6b). COPRA는 상부의 휴지기 구간(H6)에 대해서는 가장 느린 성장률로 표현하지만 이상치를 포함한 연대 자료를 사용할 경우 연구자의 주관에 의한 조절이 필요하다는 근본적인 문제점이 있다(그림 6c). 마지막으로 MOD-AGE 연대 모델은 휴지기를 상대적으로 느린 성장에 가깝게 표현한다. 특히 동굴 산호가 성장한 세 번째 휴지기 구간을 재현하지 못하며, 약 80~130 mm 사이 연대 자료의 중앙값을 반영하지 못하는 연대 모델을 작성한다(그림 6d).
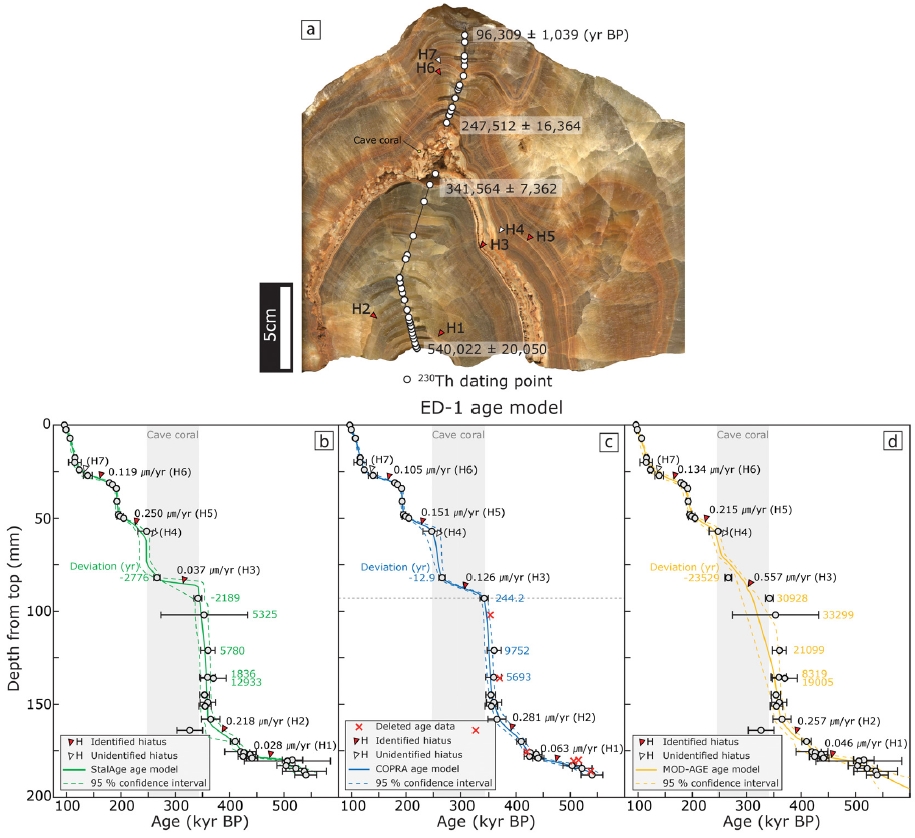
(a) A rock slab of stalagmite ED-1 showing sub-sampling points for 230Th dating. The H indicates hiatus, and red arrows are identified on the age-depth model but white one is not. (b) StalAge age-depth model. (c) COPRA age-depth model with 7 age data deleted. (d) MOD-AGE age-depth model. The deviation is the difference between the median values of the dating results and the yielded ages by algorithms.
4. 토 의
국내 석순 시료 5점의 조직적 특성과 세 가지 통계 알고리즘에 의해 작성된 연대 모델 간 대비를 통해 통계적 연대 모델 결과가 각각 다르게 나타나는 것을 확인하였다. 석순의 성장 기간 내 휴지기 없이 비교적 일률적인 성장률로 성장한 BN-1, SSN1 석순의 연대 모델 결과에서 StalAge는 성장률 변화가 거의 없는 일정한 성장률의 연대 모델을 작성하며, COPRA와 MOD-AGE는 상대적으로 연대 자료를 반영하는 연대 모델을 작성한다. 이때, COPRA 연대 모델은 성장률이 점진적으로 변화하지만 MOD-AGE는 연대측정값 부근에서 급격한 성장률 변화를 나타냄으로써 선형 보간법에 가까운 특성을 보인다. 또한 SSN1과 같이 상대적으로 개수가 적고(5점) 오차 범위가 넓은 연대자료를 사용한 연대모델에서는 MOD-AGE가 연대 자료를 가장 잘 반영하는 반면, 오차 범위가 좁고 더 많은 연대 자료(10점)를 사용한 연대 모델에서는 COPRA가 연대 자료를 가장 잘 반영한다. 이와 달리, StalAge는 SSN1, BN-1 연대모델에서 모두 다른 알고리즘에 비해 연대 자료 중앙값에서 벗어나는 연대 모델을 작성하는데, 이러한 차이는 세 연대 모델이 갖는 서로 다른 개발 철학 및 구동 특성에 의해 나타나는 결과이다. 즉, StalAge 알고리즘이 전체적인 성장 패턴에 중점을 두도록 개발되었으며, 최소 3점 이상의 선형 보간법을 기본으로 하는 몬테카를로 시뮬레이션을 수행함으로써 개별 연대 자료에 대한 가중치가 상대적으로 적어지는 방식으로 구동 되는 것이다(Scholz and Hoffmann, 2011). 결과를 종합해보면, SSN1과 같이 동굴생성물 시료의 조직적 특성이 매우 균질하고 연대자료의 정밀도가 상대적으로 낮을 경우, 주로 전체적인 성장 특성에 중점을 두는 StalAge를 선택할 수 있을 것이다. 하지만, BN-1과 같이 전반적으로 선형 성장 특성을 보이는 동시에 연대 자료의 정밀도가 상대적으로 높은 경우, 연대측정 자료의 중앙값에 가중치를 두는 COPRA 또는 MOD-AGE를 사용함으로써 각 연대측정 자료를 충분히 활용하는 방안을 선택할 수 있다. 한편, MOD-AGE를 활용할 경우에는 알고리즘 오류에 주의하여 수정하는 과정이 반드시 필요하다.
휴지기를 포함하는 DY-1, SGS1, ED-1 석순의 세 가지 통계 연대 모델에서도 마찬가지로 연속적으로 성장한 구간에서는 BN-1, SSN1의 COPRA와 MOD-AGE가 각각의 개별 연대 자료를 잘 반영하는 결과를 보인다. 그러나 MOD-AGE는 DY-1, ED-1 연대 모델에서 휴지기 구간을 지시하는 연대 자료를 모두 벗어나는 결과를 작성하며, 휴지기 구간의 성장률도 COPRA와 StalAge에 비해 빠르게 표현된다. 이는 근본적으로 MOD-AGE 알고리즘이 동굴생성물의 연속적인 성장을 전제하는 철학에 의해 제작되었기 때문에 발생하는 문제이다. 한편 StalAge는 DY-1 연대 모델에서 휴지기 구간을 세 알고리즘 중 가장 느린 성장률로 재현(그림 4b) 하지만 모든 연대 자료의 중앙값으로부터 1000~5000년 내외의 큰 편차를 갖는 신뢰하기 어려운 연대 모델을 작성한다. 이처럼 MOD-AGE와 StalAge 연대 모델에서 나타나는 휴지기 관련 문제를 해결하기 위해 휴지기를 중심으로 연대 모델을 분리하여 작성할 수 있다(Hercman and Pawlak, 2012). 이 과정에서는 반드시 조직분석에 근거한 휴지기 파악이 필요하다. 그러나 통계 알고리즘을 사용하기 위해서는 3점 이상의 연대 자료가 필요하기 때문에 휴지기를 기준으로 한 구간에 너무 집중되어 다른 구간의 연대 자료가 부족하다면 추가적인 분석이 필요할 수 있다. SGS1과 같이 최상부 부근에서 휴지기가 발생하여 추가 연대 자료를 얻는 것이 어려운 경우(그림 5a), 가능하다면 연간 성장띠 집계법 등과 같은 조직 정보를 활용하여 연대 모델을 보충할 수 있다. 종합하면, 동굴생성물 전체 성장 기간에 비해 휴지기 기간이 긴 DY-1 석순은 연대 자료의 중앙값을 가장 잘 반영하면서 휴지기 구간을 뚜렷하게 재현하는 COPRA 연대 모델이 가장 적합한 것으로 평가된다. SGS1은 최상부 또는 최하부에 휴지기가 나타나 추가적인 연대 자료 획득이 불가능한 경우에 해당하며, 모든 연대 자료를 비교적 잘 반영하고 휴지기를 최대한 재현할 수 있는 COPRA 또는 MOD-AGE 연대 모델을 활용하는 것이 가장 적합한 것으로 판단된다. 마지막으로 ED-1 석순과 같이 여러 번의 주요 휴지기를 포함하고 역전 값, 오차 범위가 넓은 측정치를 포함하는 연대 자료를 사용한 연대 모델 작성에는 StalAge가 석순의 성장 특성을 가장 잘 반영하는 결과로 판단된다.
추가적으로 COPRA는 상대적으로 복잡한 연대 자료를 사용한 연대 모델 작성이 불가능하며, 일부 연대 자료를 제거하는 과정이 필요하다. 이는 근본적으로 객관적인 연대 모델 작성을 위해 통계 알고리즘을 사용하는 목적에서 어긋난다고 볼 수 있다. 따라서 성장 특성에 관계없이 COPRA로 연대 모델 작성이 불가능한 경우, 주관적 판단에 앞서 StalAge와 MOD-AGE를 사용하는 것이 합리적이다. 또한 주로 StalAge와 MOD-AGE에서 나타나는 알고리즘 오류는 크게는 약 10배까지의 급격한 성장률 증가를 발생시켰다. 이와 같은 문제점은 고기후 연구에 있어 고해상도 프록시 자료 해석에 큰 영향을 미칠 수 있어 연구자의 주의가 필요하다.
통계적 기법을 활용한 연대 모델 작성은 선형 보간법의 단점을 보완하면서 객관성을 유지하는 연대 모델을 작성할 수 있다는 장점이 있다. 그러나 동일한 연대 자료를 사용했음에도 불구하고 선택한 통계 알고리즘에 따라서 서로 다른 연대 모델을 작성한다. 따라서 동굴생성물 연대모델 작성 시 시료 및 연대자료 특성에 알맞은 적절한 알고리즘을 선택이 필요하다. 더 나아가 각 시료의 성장 특성을 반영할 수 있는 연대 모델을 작성하기 위해서는 통계 프로그램에만 의존하지 않고 동굴생성물의 조직적 정보와 대비할 필요가 있다. 최근 들어 동굴생성물 고기후 연구에서 조직적 분석 없이 연대 자료에 통계 모델을 단순하게 적용하는 사례가 늘고 있는 실정이지만, 많은 연구자들이 동굴생성물 고기후 연구에서 조직적 분석의 필요성을 강조한 바 있다(McDermott et al., 1999; Frisia et al., 2000; Railsback et al., 2013; Martín-Chivelet et al., 2017). 세밀한 조직적 분석 결과를 바탕으로 연대 자료를 획득하고 그 결과에 통계 알고리즘을 적용하여 최종 연대 모델을 해석 및 정립한다면, 현재까지 개발된 통계 알고리즘의 활용도를 극대화할 수 있을 것이다.
5. 결 론
동굴생성물 성장 특성에 따라 적합한 통계 알고리즘을 사용한 연대 모델을 작성하기 위해 성장률 특성이 뚜렷하게 나타나는 국내 동굴생성물 5점을 선별하여 현재 동굴생성물 고기후 연구에서 널리 사용되는 통계적 연대모델 작성 알고리즘 StalAge, COPRA, MOD-AGE의 결과를 상호 비교하였다. 성장률이 비교적 일률적인 동굴생성물은 연대 자료의 정밀도가 상대적으로 높을 경우 COPRA, 낮을 경우 StalAge를 사용하는 것이 합리적인 결과를 나타냈다. 반면 휴지기를 포함하는 동굴생성물은 정밀도와 상관없이 연대 자료 및 조직적 특성에 따라 적합한 알고리즘을 선택하여 사용해야한다. 다음으로 성장 특성과 관계없이 COPRA는 상대적으로 복잡한 연대측정 자료에는 적용하기 어렵기 때문에 StalAge 또는 MOD-AGE 알고리즘을 선택할 수 있다. 그러나 전반적으로 통계적 기법에만 의존하여 작성된 연대모델은 동굴생성물의 세밀한 성장유형 특성을 반영하는데 한계가 있다. 따라서 상세한 연대 모델 작성을 위해서는 휴지기를 지시하는 조직적 특성 파악, 연간 성장띠 집계법 등과 같은 상세한 조직적 분석이 반드시 전제되어야 한다. 이 연구의 결과는 주어진 조건에서 가장 합리적인 연대 모델을 작성하는데 필요한 기초 정보를 제공하며, 나아가 더 정밀하고 정확한 고기후 연구에 기여할 수 있을 것으로 기대된다. 이번 연구에서는 성장 유형 특성이 뚜렷하게 나타나는 5점의 동굴생성물에 한하여 평가를 진행하였지만 더욱 세밀한 분석을 위해서 세분화된 성장 유형 분류와 더 많은 동굴생성물 표본에 대한 연대 모델 비교가 필요할 것으로 사료된다.
Acknowledgments
이 연구는 2019년 정부(과학기술정보통신부)의 재원으로 한국연구재단(NRF)의 지원을 받아 수행된 신진연구자지원사업(No. NRF-2016R1C1B2016525), 재도약연구사업(No. NRF-2019R1H1A1101097)의 일환으로 수행되었다.
References
-
Arienzo, M.M., Swart, P.K., Broad, K., Clement, A.C., Pourmand, A. and Kakuk, B., 2017, Multi-proxy evidence of millennial climate variability from multiple Bahamian speleothems. Quaternary Science Reviews, 161, 18-29.
[https://doi.org/10.1016/j.quascirev.2017.02.004]

-
Blaauw, M., 2010, Methods and code for ‘classical’ age-modelling of radiocarbon sequences. Quaternary Geochronology, 5, 512-518.
[https://doi.org/10.1016/j.quageo.2010.01.002]

-
Blaauw, M. and Christen, J.A., 2005, Radiocarbon peat chronologies and environmental change. Journal of the Royal Statistical Society: Series C (Applied Statistics), 54, 805-816.
[https://doi.org/10.1111/j.1467-9876.2005.00516.x]

-
Blaauw, M. and Christen, J.A., 2011, Flexible paleoclimate age-depth models using an autoregressive gamma process. Bayesian analysis, 6, 457-474.
[https://doi.org/10.1214/ba/1339616472]

-
Breitenbach, S.F.M., Rehfeld, K., Goswami, B., Baldini, J.U.L., Ridley, H.E., Kennett, D.J., Prufer, K.M., Aquino, V.V., Asmerom, Y., Polyak, V.J., Cheng, H., Kurths, J. and Marwan, N., 2012, COnstructing proxy records from age models (COPRA). Climate of the Past, 8, 1765-1779.
[https://doi.org/10.5194/cp-8-1765-2012]

-
Caddeo, G.A., Railsback, L.B., De Waele, J. and Frau, F. 2015, Stable isotope data as constraints on models for the origin of coralloid and massive speleothems: the interplay of substrate, water supply, degassing, and evaporation. Sedimentary Geology, 318, 130-141.
[https://doi.org/10.1016/j.sedgeo.2014.12.008]

-
Cheng, H., Edwards, R.L., Shen, C.-C., Polyak, V.J., Asmerom, Y., Woodhead, J., Hellstrom, J., Wang, Y., Kong, X., Spötl, C., Wang, X. and Alexander Jr, E.C., 2013, Improvements in 230Th dating, 230Th and 234U half-life values, and U-Th isotopic measurements by multi-collector inductively coupled plasma mass spectrometry. Earth and Planetary Science Letters, 371, 82-91.
[https://doi.org/10.1016/j.epsl.2013.04.006]

-
Cleveland, W.S. and Devlin, S.J., 1988, Locally weighted regression: an approach to regression analysis by local fitting. Journal of the American statistical association, 83, 596-610.
[https://doi.org/10.1080/01621459.1988.10478639]

-
Dorale, J.A., Edwards, R.L., Alexander Jr, E.C., Shen, C.-C., Richards, D.A. and Cheng, H., 2007, Uranium-series dating of speleothems: current techniques, limits, & applications. In Studies of Cave Sediments: Physical and Chemical Records of Paleoclimate, 177-197.
[https://doi.org/10.1007/978-1-4020-5766-3_10]

-
Frisia, S., Borsato, A., Fairchild, I.J. and McDermott, F., 2000, Calcite fabrics, growth mechanisms, and environments of formation in speleothems from the Italian Alps and southwestern Ireland. Journal of Sedimentary Research, 70, 1183-1196.
[https://doi.org/10.1306/022900701183]

-
Heegaard, E., Birks, H.J.B. and Telford, R.J., 2005, Relationships between calibrated ages and depth in stratigraphical sequences: an estimation procedure by mixed-effect regression. The Holocene, 15, 612-618.
[https://doi.org/10.1191/0959683605hl836rr]

-
Hercman, H. and Pawlak, J., 2012, MOD-AGE: An age-depth model construction algorithm. Quaternary Geochronology, 12, 1-10.
[https://doi.org/10.1016/j.quageo.2012.05.003]

- Jo, K., Woo, K.S., Kim, J.C., Yang, D.Y., Edwards, R.L., Cheng, H. and Wang, Y., 2006, Paleoclimatic implications recorded in the late Pleistocene stalagmite, Eden Cave, Danyang, Korea. Journal of the Geological Society of Korea, 42, 127-142 (in Korean with English abstract).
-
Jo, K., Woo, K.S., Lim, H.S., Cheng, H., Edwards, R.L., Wang, Y., Jiang, X., Kim, R., Lee, J.I., Yoon, H.I. and Yoo, K.-C., 2011, Holocene and Eemian climatic optima in the Korean Peninsula based on textural and carbon isotopic records from the stalagmite of the Daeya Cave, South Korea. Quaternary Science Reviews, 30, 1218-1231.
[https://doi.org/10.1016/j.quascirev.2011.02.012]

-
Jo, K., Woo, K.S., Yi, S., Yang, D.Y., Lim, H.S., Wang, W., Cheng, H. and Edwards, R.L., 2014, Mid-latitude interhemispheric hydrologic seesaw over the past 550,000 years. Nature, 508, 378-382.
[https://doi.org/10.1038/nature13076]

-
Jo, K., Yi, S., Lee, J.Y., Woo, K.S., Cheng, H., Edwards, L.R. and Kim, S.T., 2017, 1000-year quasi-periodicity of weak monsoon events in temperate northeast Asia since the mid-holocene. Scientific Reports, 7, 1-9.
[https://doi.org/10.1038/s41598-017-15566-4]

-
Liu, D., Wang, Y., Cheng, H., Edwards, R.L., Kong, X. and Li, T.Y., 2016, Strong coupling of centennial-scale changes of Asian monsoon and soil processes derived from stalagmite δ18O and δ13C records, southern China. Quaternary Research, 85, 333-346.
[https://doi.org/10.1016/j.yqres.2016.02.008]

-
Martín-Chivelet, J., Muñoz-García, M.B., Cruz, J.A., Ortega, A.I. and Turrero, M.J., 2017, Speleothem Architectural Analysis: Integrated approach for stalagmite-based paleoclimate research. Sedimentary Geology, 353, 28-45.
[https://doi.org/10.1016/j.sedgeo.2017.03.003]

-
McDermott, F., 2004, Palaeo-climate reconstruction from stable isotope variations in speleothems: a review. Quaternary Science Reviews, 23, 901-918.
[https://doi.org/10.1016/j.quascirev.2003.06.021]

-
McDermott, F., Frisia, S., Huang, Y., Longinelli, A., Spiro, B., Heaton, T.H.E., Hawkesworth, C.J., Borsato, A., Keppens, E., Fairchild, I.J., Borg, K., Verheyden, S. and Selmo, E., 1999, Holocene climate variability in Europe: evidence from δ18O, textural and extension-rate variations in three speleothems. Quaternary Science Reviews, 18, 1021-1038.
[https://doi.org/10.1016/S0277-3791(98)00107-3]

-
Mehterian, S., Pourmand, A., Sharifi, A., Lahijani, H.A., Naderi, M. and Swart, P.K., 2017, Speleothem records of glacial/interglacial climate from Iran forewarn of future Water Availability in the interior of the Middle East. Quaternary Science Reviews, 164, 187-198.
[https://doi.org/10.1016/j.quascirev.2017.03.028]

-
Mori, T., Kashiwagi, K., Amekawa, S., Kato, H., Okumura, T., Takashima, C., Wu, C.-C., Shen, C.-C., Quade, J. and Kano, A., 2018, Temperature and seawater isotopic controls on two stalagmite records since 83 ka from maritime Japan. Quaternary Science Reviews, 192, 47-58.
[https://doi.org/10.1016/j.quascirev.2018.05.024]

-
Railsback, L.B., Akers, P.D., Wang, L., Holdridge, G.A. and Voarintsoa, N.R., 2013, Layer-bounding surfaces in stalagmites as keys to better paleoclimatological histories and chronologies. International Journal of Speleology, 42, 167-180.
[https://doi.org/10.5038/1827-806X.42.3.1]

-
Scholz, D. and Hoffmann, D.L., 2011, StalAge-An algorithm designed for construction of speleothem age models. Quaternary Geochronology, 6, 369-382.
[https://doi.org/10.1016/j.quageo.2011.02.002]

-
Scholz, D., Hoffmann, D.L., Hellstrom, J. and Ramsey, C.B., 2012, A comparison of different methods for speleothem age modelling. Quaternary Geochronology, 14, 94-104.
[https://doi.org/10.1016/j.quageo.2012.03.015]

-
Telford, R.J., Heegarrd, E. and Briks, H.J.B., 2004, All age-depth models are wrong: but how badly?. Quaternary Science Reviews, 23, 1-5.
[https://doi.org/10.1016/j.quascirev.2003.11.003]

-
Trachsel, M. and Telford, R.J., 2017, All age-depth models are wrong, but are getting better. The Holocene, 27, 860-869.
[https://doi.org/10.1177/0959683616675939]