Statistical analyses of volcanic gas data
Abstract
In this study, a series of statistical approaches were discussed to interpret volcanic gas data for the better prediction of volcanic eruptions. These approaches included data modification, parameter selection, and time series analysis. In case of data modification, raw gas data were first transformed into evenly spaced time series by linear interpolation, and then standardized into dimensionless forms. During parameter selection, a large data set was reduced into a smaller one using factor analysis, with the aid of correlation and cross correlation analyses. In time series analysis, the selected data were disintegrated into three components (random, periodic, and trend components) using the Classical Decomposition with Moving Averages (CDMA) and/or spectra analyses. Finally, in-depth discussions were provided on how to interpret the extracted trend components to predict volcanic eruptions. These approaches may provide a systematic way to interpret volcanic gas data. The practice of the aforementioned analyses is of critical importance given that the precursory signals of eruptions tend to be mingled with non-volcanological backgrounds.
초록
본 연구는 화산의 분화 시기를 예측하기 위해 일련의 통계기법을 토대로 화산가스 자료를 해석하는 방법을 소개한다. 사용된 통계기법은 ‘자료변형’, ‘인자선택’, ‘시계열분석’의 세 단계로 구분된다. 1단계에서 측정된 자료는 선형 보간(linear interpolation)에 의해 등시계열(evenly spaced time series)로 변형되고, 이후 무차원 계열(dimensionless series)로 바뀐다. 2단계에서 다수의 자료들은 요인분석(factor analysis)을 비롯해 상관분석(correlation analysis)과 교차상관분석(cross correlation analysis)을 바탕으로 소수 자료로 축소해 추후 분석에 사용된다. 3단계에서 선택된 자료는 Classical Decomposition with Moving Averages (CDMA) 및 주파수 분석(spectra analyses)에 의해 우연성분(periodic component), 주기성분(periodic component), 추세성분(trend component)으로 분리할 수 있다. 마지막으로 추출된 추세성분을 사용해 화산분화 예측에 대해 토의했다. 분화 징후를 지시하는 신호가 종종 비화산적 배경 신호와 혼재함을 고려할 때, 본 연구에서 제시된 통계분석은 화산가스 자료를 해석하는 데 있어 체계적이고 유용한 방법을 제공할 수 있다.
Keywords:
volcanic gas, volcanic eruption, factor analysis, time series analysis키워드:
화산가스, 화산분화, 요인분석, 시계열분석1. INTRODUCTION
Volcanic eruptions often lead to the damage of human lives and properties, and they may also trigger climate changes (Robock, 2000). Accordingly, the prediction of volcanic eruptions in a timely manner can reduce or prevent these adverse consequences. Several methods have been employed to aid the prediction of volcanic eruptions, which include electronic distance measurement (EDM) (Ramírez-Ruiz et al., 2002; Saepuloh et al., 2013), seismological monitoring (Ratdomopurbo and Poupinet, 2000; Inza et al., 2014), electric and magnetic field measurement (Sasai et al., 2002; Lillis et al., 2008), and volcanic gas monitoring (Inguaggiato et al., 2013). Of all these methods, volcanic gas monitoring is based on temporal changes in volcanic gas compositions caused by volcanic activities.
As a magma ascends near the ground surface, volatile components within it tend to be exsolved and discharged as gases (Proussevitch and Sahagian, 2005). In general, volcanic gas emission gets stronger as eruptions become imminent (Fischer et al., 1996). Thus, highly elevated CO2, SO2, and H2S concentrations in volcanic gases are often considered to be indicative of volcanic eruptions (Bruno et al., 2001; Werner et al., 2013). Due to the varied solubility in magmas, each volcanic gas has a different propensity to be exsolved; for example, less soluble components (e.g., CO2) emit readily from the early stage of eruptions, whereas more soluble components (e.g., HCl and HF) do not emit strongly till the later stage (Lee et al., 2018). To this end, the concentration ratios of CO2/H2O, CO2/SO2, SO2/HCl, and SO2/HF have also been regarded as eruption precursors (Aiuppa, 2009; Allard, 2010; Notsu and Mori, 2010; López et al., 2013; Werner et al., 2013).
Despite the aforementioned trends in volcanic gas compositions, the interactions of volcanic gases with hydrothermal systems (e.g., groundwater) and the meteorological conditions may alter them to significant extents (Shimoike and Notsu, 2000; Lee et al., 2018). More importantly, precursory signals of eruptions may be not readily discerned from background fluctuations. For example, Giammanco et al. (2013) found that elevated CO2 fluxes prior to the eruptions of Etna volcano (an active stratovolcano on the east coast of Sicily in Italy) were only within the range encountered during the quiescent period. Also, significant temporal variations in volcanic gas compositions were detected during quiescent periods (Shimoike and Notsu, 2000; Zimmer and Erzinger, 2003; Shinohara, 2005). Furthermore, remote measurements of volcanic gases are inevitably affected by the atmospheric conditions, making the collected data likely mingled with metrological components. For example, at Izu-Oshima volcano (a volcanic island in the Izu archipelago in the Philippine Sea), volcanic CO2 concentration was negatively correlated with the atmospheric pressure, and volcanic O2 concentration was positively correlated with it (Shimoike and Notsu, 2000). Therefore, when interpreting volcanic gas data, it is necessary to separate volcanological signatures from non-volcanological noises for the better assessment of eruptive events. To this end, a series of statistical approaches were proposed here, which included data modification, parameter selection, and time series analysis. With the proposed approaches, it is possible to extract random, periodic, and trend components from volcanic gas data in order to interpret them in a systematic way.
2. MATERIALS AND METHODS
Monitoring of volcanic gases at active volcanoes has been mostly conducted using discontinuous techniques with relatively long intervals (e.g., weeks to months), or it has been limited to single gas parameters (Benhamou et al., 1988; Connor et al., 1993; Cigolini et al., 2001). As a result, only a few of previous works related to volcanic gas chemistry have produced multiple sets of continuous data with relatively short intervals (e.g., hours to days), which are suitable for statistical analyses. Through extensive research, the volcanic gas data from Stromboli volcano (Aiuppa et al., 2010) and Merapi volcano (Zimmer and Erzinger, 2003) were subjected to the proposed statistical approaches (see Figs. 1a and 1b for the original data).
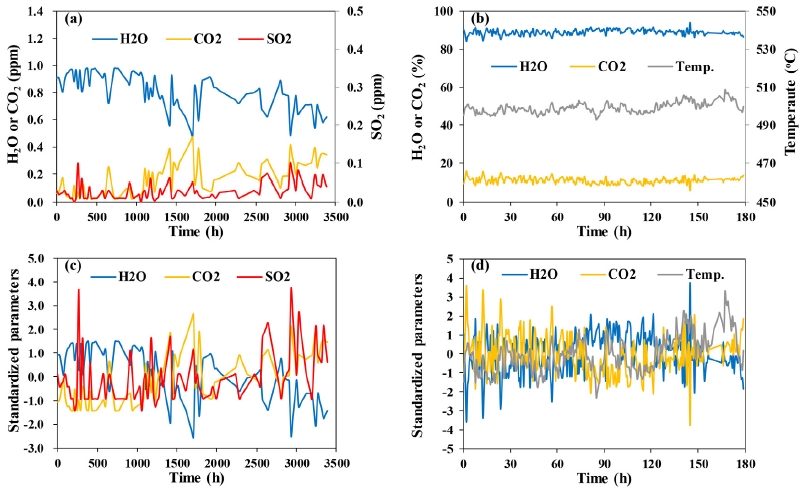
Volcanic H2O, CO2, and SO2 concentrations at Stromboli volcano (Aiuppa et al., 2010) (a), volcanic H2O, CO2, and temperature at Merapi volcano (Zimmer and Erzinger, 2003) (b), evenly spaced and standardized time series of part (a) (c), and evenly spaced and standardized time series of part (b) (d).
Stromboli volcano, an active basaltic volcano in Italy, is characterized by the mild and uninterrupted Strombolian activity (Rosi et al., 2000). Collected with a remote sensing MultiGAS (multicomponent gas analyzer system), the data from this volcano is composed of volcanic H2O, CO2, and SO2 concentrations over the period of July to December 2008 at the monitoring interval of several days (Aiuppa et al., 2010). Significant variations in the gas compositions at this volcano were attributed to the dynamic nature of magmatic degassing (Aiuppa et al., 2010). Merapi volcano, an andesitic volcano, is located on the Java Arc, where the Indo-Australian Plate is subducted beneath the Java Trench (Widiyantoro and van der Hilst, 1996). The data set from this volcano consist of gas temperature as well as volcanic H2O and CO2 concentrations over several weeks at the interval of ~35 min (Zimmer and Erzinger, 2003). These data were collected in a real-time mode using a thermocouple and a gas chromatography that were directly connected to a fumarole (Zimmer and Erzinger, 2003). Significant variations in the composition and temperature of volcanic gases at this volcano resulted from regular degassing and meteorological variability (Zimmer and Erzinger, 2003).
Volcanic gas data are often unevenly spaced time series in which the interval between observations is not the same. A common way to deal with unevenly spaced time series is to transform them into evenly spaced time series using interpolation methods, among which linear interpolation is commonly used. As such, linear interpolation was employed here to convert unevenly spaced data into evenly spaced ones:
| (1) |
where pi-1, pi, and pi+1 are the measured properties at time ti-1, ti, and ti+1, respectively. Note that the transformation of time series data using interpolation methods may introduce significant biases and errors in some cases (Rehfeld et al., 2011). Thus, if significant irregularity in time spacing is present or considerable amounts of data are missing, it is better to use the statistical methods specifically designated for unevenly spaced time series. Once the interpolation is complete, the resultant evenly spaced data can be processed using statistical tools intended for evenly spaced time series.
In general, a greater emphasis is placed on a time series having a higher variance (i.e., large temporal fluctuations) than that having a lower variance. Accordingly, each time series in Figs. 1a and 1b was standardized using its mean and standard deviation before the subsequent analyses. Furthermore, when dealing with the data in different units (e.g., H2O and CO2 concentrations versus gas temperature in Fig. 1b), it is mandatory to make standardization of them. In this study, the evenly spaced and standardized time series in Figs. 1c and 1d were processed using statistical analyses including factor analysis, correlation analysis, cross correlation analysis, and time series analysis. Some of these analyses were carried out using Microsoft Excel 2016 with the XLSTAT package. The other analyses including time series analysis were conducted using the Classical Decomposition with Moving Averages (CDMA) analysis, available at a website free of charge (Wessa, 2017).
3. RESULTS AND DISCUSSION
3.1 Parameter selection
First of all, factor analysis was employed to determine the number of factors (i.e., processes) required to explain the variance among a multiple of time series (Lawrence and Upchurch, 1982). Note that a factor does not necessarily correspond to a specific process, and rather that it may represent a combination of several processes. In case that multiple volcanic gas parameters (e.g., concentrations of CO2, H2O, SO2, H2S, etc.) are available, it is possible to reduce a large set of data into a smaller one based on factor analysis.
Table 1 presents the results of factor analysis for the data in Fig. 1c and 1d. As indicated by the cumulative proportions, Factors 1 and 2 in both data sets can explain nearly all of the variance among the volcanic gas parameters, with the minimal proportion of Factor 3. Accordingly, only two series are worthy for the subsequent analyses. In both sets, H2O concentrations have positive loadings of Factors 1 and 2, whereas CO2 concentrations have negative loadings of Factors 1 and 2. These suggest the opposite trend between H2O and CO2 concentrations. Indeed, the time series of H2O concentrations are negatively correlated with those of CO2 concentrations (see Fig. 2a and 2b). In case of Merapi volcano, the time series of CO2 concentrations is just a mirror image of that of H2O concentrations given that the slope of the corresponding regression line is -1.000 with R = -1.000 (R2 = 1.000) in Fig. 2b.
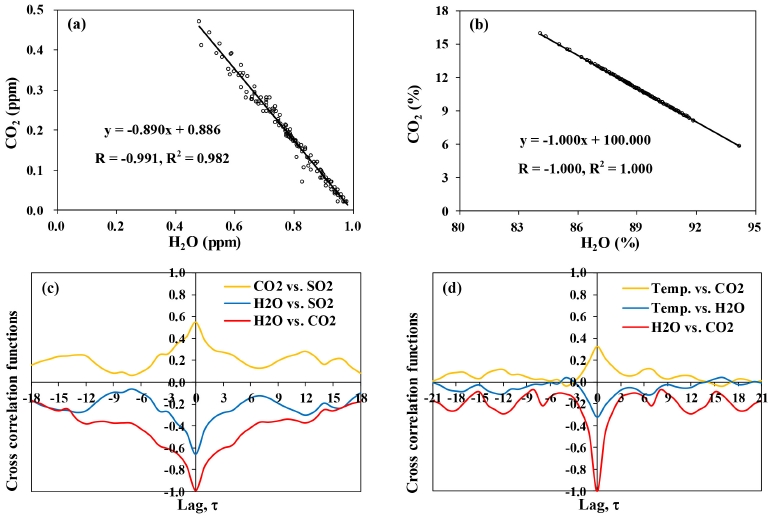
Correlation analysis between H2O and CO2 concentrations at Stromboli volcano (Aiuppa et al., 2010) (a) and at Merapi volcano (Zimmer and Erzinger, 2003) (b), and cross correlation analysis of volcanic gas data at Stromboli volcano (Aiuppa et al., 2010) (c) and at Merapi volcano (Zimmer and Erzinger, 2003) (d).
As mentioned above, two time series need to be selected in the present examples. Then, which ones are to be selected? Before answering this question, one should perform cross correlation analysis, which measures the similarity between two series as a function of lag (τ), the temporal displacement between them (Larocque et al., 1998). This analytical tool is available at a website free of charge (Wessa, 2017). By cross correlation analysis, it is possible to evaluate whether there is a stimulus-response relationship between two time series. Fig. 2c and 2d show the results of cross correlation analysis between volcanic gas data in Fig. 1c and 1d. In Fig. 2c and 2d, the highest or lowest values of cross correlation functions (CCF) occur at τ = 0, indicating that there is no stimulus-response relationship among the time series under consideration. Nonetheless, such relationships may be present in the data obtained by remote sensing techniques since the compositions of volcanic gas plumes are inevitably affected by atmospheric temperature and pressure, wind speed and direction, and precipitation (refer to section 3.3 in Lee et al. (2018)). For example, Shimoike and Notsu (2000) have found that volcanic O2 concentration is positively correlated with the atmospheric pressure with several hour displacement. In their case, if the O2 concentration profile is shifted to several hours earlier along the time axis, the resultant profile will match that of the atmospheric pressure. Thus, it should be noted that one cannot select any time series having stimulus-response relationships.
When choosing the parameters, a priority should be given to those that are predominantly loaded by single factors. As can be seen in Table 1, no parameters meet this criterion. Then, CO2 and H2S concentrations are usually good choices since both species are least affected by the groundwater scrubbing (Symonds et al., 2001). Given the dilution of volcanic gases by water vaporization and boiling during their ascents (Lee et al., 2018), it is often necessary to normalize these concentrations with respect to volcanic H2O concentration. In the present examples, thus, the concentration ratios of CO2/H2O are selected. Importantly, this selection can prevent the strongly inter-correlated parameters (H2O and CO2 concentrations) from being considered together for the subsequent analyses.
In the present examples, one still needs to select one more parameter from both data sets. The concentration ratios of CO2/SO2, CO2/HCl, CO2/HF, SO2/HCl, and SO2/HF have been often used to predict volcanic eruptions (Duffell et al., 2003; Aiuppa, 2009; Notsu and Mori, 2010; Stremme et al., 2011; López et al., 2013). Notably, individual gas concentrations may fluctuate significantly in response to non-volcanological effects such as hydrothermal interactions and meteorological conditions (Shimoike and Notsu, 2000; Symonds et al., 2001). Thus, to lessen non-volcanological effects, it is good to use the concentration ratios with the expectation that such effects have an influence on individual gas concentrations in a similar way. More importantly, the ratios are more likely to reach either maxima or minima prior to volcanic eruptions than individual gas concentrations (refer to section 4.3 in Lee et al. (2018)). For the data set of Aiuppa et al. (2010), the CO2/SO2 ratio is the only remaining one on the aforementioned list. If more than one ratio is available, one may consider the ratio wherein two gas concentrations are characterized by the same highest loading factor but by different secondary factors, and then move to the one wherein two gas concentrations have different highest loading factors but the same secondary factor. In case of Zimmer and Erzinger (2003), volcanic gas temperature is to be chosen since no more concentration ratio is available after selecting CO2/H2O ratios.
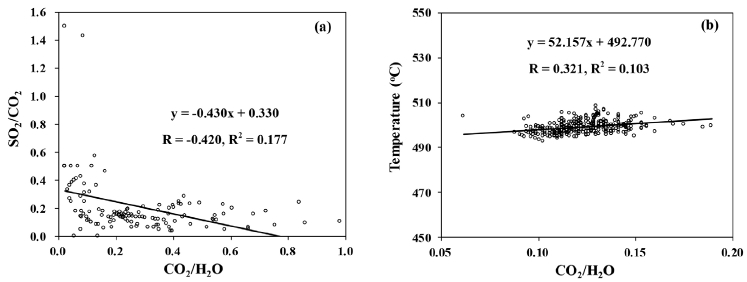
Once all parameters are selected, one should make sure that they are not correlated with each other. As shown in Fig. 3a, the ratios of CO2/H2O and SO2/CO2 are not strongly correlated (R = -0.420). Also, in Fig. 3b, the ratios of CO2/H2O are not strongly correlated with volcanic gas temperature (R = 0.321). These results assure the validity of the selected parameters for the subsequent analyses. If selected parameters are correlated significantly, one should try other parameters and repeat correlation analysis until no strong correlation exists among them.
3.2 Time series analysis
Time series of selected parameters can be processed using a multiple of statistical tools, each of which has its own pros and cons. In this study, the selected time series were subjected to the Classical Decomposition with Moving Averages (CDMA) analysis (Wessa, 2017). This statistical tool can provide a convenient and effective way to extract trend, periodic, and random components from time series (see Fig. 4 and 5). In volcanic gas analysis, the trend component reflects the depth (pressure) of magmatic degassing and the extent of hydrothermal interactions, the key processes controlling the evolution of volcanic gas compositions (Lee et al., 2018). Note that the trend component may be long-term or short-term depending on the monitoring duration. For example, while Fig. 4a and 4b show several month long trends, Fig. 5a and 5b indicate the trends over several days. The periodic component likely represents regular rises of gas bubbles from magmas as well as diurnal and season variations in metrological conditions. The random component may result from explosive gas discharges, gas influxes from other magma sources, vent collapses due to seismic activities, and abrupt changes in metrological conditions.
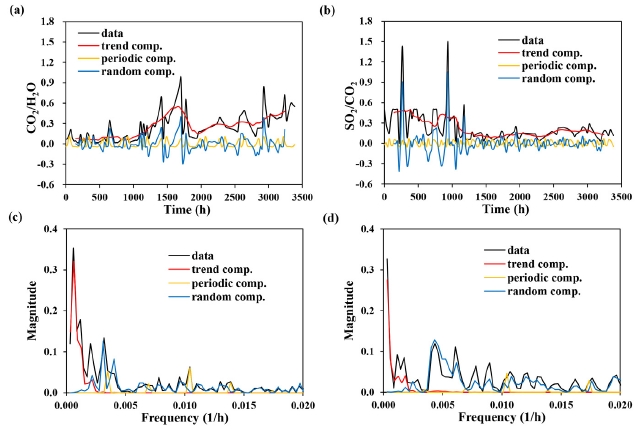
Time series analysis of CO2/H2O ratios (a) and SO2/CO2 ratios (b) by Classical Decomposition with Moving Averages (CDMA) analysis at the period (n) of 12, and the corresponding periodograms of CO2/H2O ratios (c) and SO2/CO2 ratios (d) by spectral analysis. The original data were collected at Stromboli volcano (Aiuppa et al., 2010).
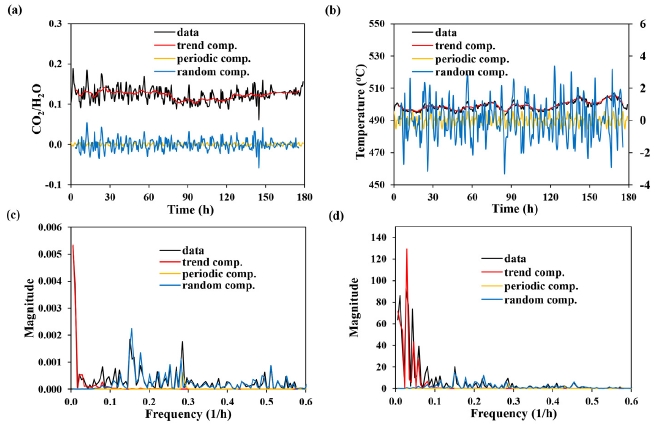
Time series analysis of CO2/H2O ratios (a) and temperature (b) by Classical Decomposition with Moving Averages (CDMA) analysis at the period (n) of 12, and the corresponding periodograms of CO2/H2O ratios (c) and temperature (d) by spectral analysis. The original data were collected at Merapi volcano (Zimmer and Erzinger, 2003).
In the CDMA analysis, one is first asked to select the period (n), the size of subset data to be averaged. In Fig. 6, it is illustrated how the period affects the apportionment among the three components. With the increasing period, the trend component becomes smoother, with the greater proportion of the other components (see Fig. 6). When choosing the period in the CDMA analysis, one should take into account the monitoring length and interval. For example, if monthly measurements are made over a few years, the seasonal periodicity (n = 12) need to be reflected. On the other hand, when the collected data are several days long with hourly intervals, the diurnal periodicity (n = 24) should be considered. Also, it is better to choose a larger period in analyzing a bigger size of data.
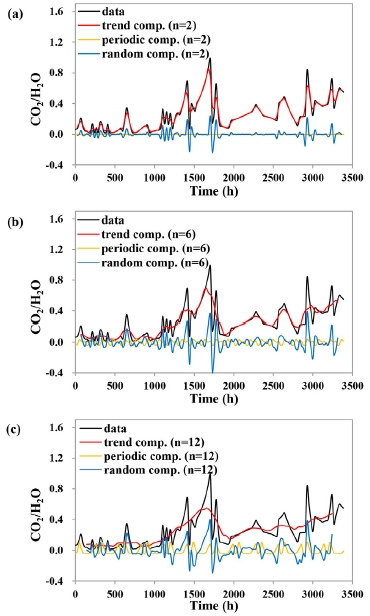
Effect of the period (n) on the apportionment among the trend, periodic, and random components in the time series of CO2/H2O ratios by the CDMA analysis. The original data were collected at Stromboli volcano (Aiuppa et al., 2010).
Once the trend component is separated from the other components, it is necessary to evaluate whether it is significant compared to the seasonal and random components. In Fig. 4a and 4b, the ranges (i.e., spreads) of the trend components are greater than those of the other components. Thus, one may claim that the ratios of volcanic CO2/H2O and SO2/CO2 at Stromboli volcano were roughly on the upward and downward, respectively. In contrast, the trend components in Fig. 5a and 5b are largely within the ranges of the other components. Thus, despite the significant temporal variations in both CO2/H2O ratios and temperature, no definite trend was noted at Merapi volcano.
Despite the preceding discussion, it is not certain which feature(s) in the trend components can herald volcanic eruptions. Although this issue may not be resolved completely, it is still possible to glean an important clue. In general, abrupt changes in volcanic gas compositions precede eruptions (Lee et al., 2018), suggesting that the rates of changes in volcanic gas compositions are of potential importance in predicting eruptions. In this study, the rates of changes in CO2/H2O and SO2/CO2 ratios at Stromboli volcano were calculated for the trend components as follows:
| (2) |
where Ri and Ri+1 are the concentration ratios of CO2/H2O or SO2/CO2 at time ti. and ti+1, respectively. In Fig. 7, the calculated rates are compared to their 75th and 95th percentiles as well as the means. If the rates lie successively beyond a limit (e.g., 95th percentile), such features may be considered a sign of eruptions. In Fig. 7, it should be noted that the data located outside a cautionary limit (e.g., 95th percentile) do not necessarily foretell imminent eruptions since only a small amount of data are incorporated in these calculations. Thus, volcanic gas data monitored over a longer period are required for the better prediction of eruptions. Also, it is beneficial to have the data encompassing previous eruption events in order to determine to what extents the rates of changes in volcanic gas compositions may occur close to eruptions.
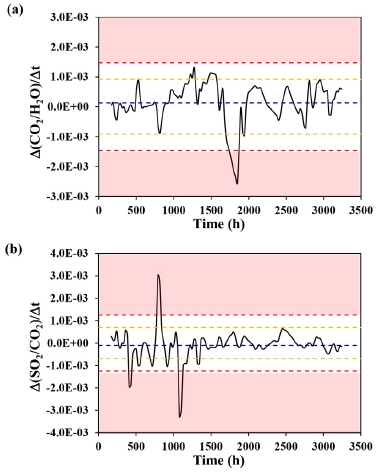
Rates of changes in the trend components of CO2/H2O ratios (a) and SO2/CO2 ratios (b). The data sources of parts (a) and (b) are Figs. 4a and 4b, respectively. Dashed lines in red, orange, and blue represent 95th percentiles, 75th percentiles, and means, respectively.
In addition to CDMA analysis, time series can be processed and evaluated using spectral analysis, by which the data in a time domain are Fourier-transformed into those in a frequency domain (Spongberg, 2000). This statistical tool is also available at a website free of charge (Wessa, 2017). The resultant diagram obtained by this analysis is called a periodogram, in which the signals at low frequencies correspond to long-term changes whereas those at high frequencies reflect short-lived fluctuations. In Figs. 4c-4d and 5c-5d, three components as well as the standardized data are subjected to spectral analysis. It is obvious that the signals at low frequencies match the trend components and those at intermediate to high frequencies match the periodic and/or random components. In Figs. 4c-4d and 5c-5d, the signals at low frequencies are far stronger than those at high frequencies, indicating the dominance of the trend components. Also, the periodic components are shown to be weaker compared to the other components. Yet, the situations may arise that the signals at high frequencies are as strong as or stronger than those at low frequencies. Even in such cases, it is possible to selectively extract the trend components by back-transforming the signals at low frequencies in a periodogram. Although not further discussed, such back-transformation is commonly exercised to filter out noises (i.e., high frequency signals) from time series (Spongberg, 2000).
4. CONCLUSIONS
Volcanic gas compositions are affected by multiple factors including magmatic processes, hydrothermal interactions, and meteorological conditions (Shimoike and Notsu, 2000; Symonds et al., 2001). Due to the site specificity and temporal variability of these factors, it is often challenging to make generalizations about volcanic gas chemistry to predict volcanic eruptions. Thus, there is a strong need to develop a systematic way to analyze volcanic gas data. In this study, a series of statistical approaches were proposed to interpret volcanic gas data in a simple but robust way. Also, example cases were brought up to aid implement the proposed approaches. Using such approaches, it is possible to separate volcanological signals from non-volcanological backgrounds in volcanic gas data. Thus, one may have a better view of magmatic processes to forecast volcanic eruptions and assess the hazard and risk associated with them.
Acknowledgments
This work was supported by a 2-Year Research Grant of Pusan National University.
References
-
Aiuppa, A., (2009), Degassing of halogens from basaltic volcanism: insights from volcanic gas observations, Chemical Geology, 263, p99-109.
[https://doi.org/10.1016/j.chemgeo.2008.08.022]

-
Aiuppa, A., Bertagnini, A., Métrich, N., Moretti, R., di Muro, A., Liuzzo, M., and Tamburello, G., (2010), A model of degassing for Stromboli volcano, Earth and Planetary Science Letters, 295, p195-204.
[https://doi.org/10.1016/j.epsl.2010.03.040]

-
Allard, P., (2010), A CO2-rich gas trigger of explosive paroxysms at Stromboli basaltic volcano, Italy, Journal of Volcanology and Geothermal Research, 189, p363-374.
[https://doi.org/10.1016/j.jvolgeores.2009.11.018]

-
Benhamou, G., Allard, P., Sabroux, J.C., Vitter, G., Dajlevic, D., and Creusot, A., (1988), Oxygen fugacity of gases and rocks from Momotombo volcano, Nicaragua: application to volcanological monitoring, Journal of Geophysical Research, 93(B12), p14872-14880.
[https://doi.org/10.1029/jb093ib12p14872]

-
Bruno, N., Caltabiano, T., Giammanco, S., and Romano, R., (2001), Degassing of SO2 and CO2 at Mount Etna (Sicily) as an indicator of pre-eruptive ascent and shallow emplacement of magma, Journal of Volcanology and Geothermal Research, 110, p137-153.
[https://doi.org/10.1016/s0377-0273(01)00201-3]

-
Cigolini, C., Salierno, F., Gervino, G., Bergese, P., Marino, C., Russo, M., Prati, P., Ariola, V., Bonetti, R., and Begnini, S., (2001), High-resolution radon monitoring and hydrodynamics of Mount Vesuvius, Geophysical Research Letters, 28, p4035-4038.
[https://doi.org/10.1029/2000gl012775]

-
Connor, C.B., Clement, B.M., Song, X.D., Lane, S.B., and West-Thomas, J., (1993), Continuous monitoring of high-temperature fumaroles on an active lava dome. Volcán Colima, Mexico: evidence of mass flow variation in response of atmospheric forcing, Journal of Geophysical Research, 98(B11), p19713-19722.
[https://doi.org/10.1029/93jb02169]

-
Duffell, H.J., Oppenheimer, C., Pyle, D.M., Galle, B., McGonigle, A.J.S., and Burton, M.R., (2003), Changes in gas composition prior to a minor explosive eruption at Masaya volcano, Nicaragua, Journal of Volcanology and Geothermal Research, 126, p327-339.
[https://doi.org/10.1016/s0377-0273(03)00156-2]

-
Fischer, T.P., Arehart, G.B., Sturchio, N.C., and Williams, S.N., (1996), The relationship between fumarole gas composition and eruptive activity at Galeras volcano, Colombia, Geology, 24, p531-534.
[https://doi.org/10.1130/0091-7613(1996)024<0531:trbfgc>2.3.co;2]

-
Giammanco, S., Neri, M., Salerno, G.G., Caltabiano, T., Burton, M.R., and Longo, V., (2013), Evidence for a recent change in the shallow plumbing system of Mt. Etna (Italy): gas geochemistry and structural data during 2001-2005, Journal of Volcanology and Geothermal Research, 251, p90-97.
[https://doi.org/10.1016/j.jvolgeores.2012.06.001]

-
Inguaggiato, S., Jácome Paz, M.P., Mazot, A., Delgado Granados, H., Inguaggiato, C., and Vita, F., (2013), CO2 output discharged from Stromboli Island (Italy), Chemical Geology, 339, p52-60.
[https://doi.org/10.1016/j.chemgeo.2012.10.008]

-
Inza, L.A., Métaxian, J.P., Mars, J.I., Bean, C.J., O`Brien, G.S., Macedo, O., and Zandomeneghi, D., (2014), Analysis of dynamics of vulcanian activity of Ubinas volcano, using multicomponent seismic antennas, Journal of Volcanology and Geothermal Research, 270, p35-52.
[https://doi.org/10.1016/j.jvolgeores.2013.11.008]

-
Larocque, M., Mangin, A., Razack, M., and Banton, O., (1998), Contribution of correlation and spectra analyses to the regional study of a large karst aquifer (Charente, France), Journal of Hydrology, 205, p217-231.
[https://doi.org/10.1016/s0022-1694(97)00155-8]

-
Lawrence, F.W., and Upchurch, S.B., (1982), Identification of recharge areas using geochemical factor analysis, Groundwater, 20, p680-687.
[https://doi.org/10.1111/j.1745-6584.1982.tb01387.x]

-
Lee, S., Kang, N., Park, M., Hwang, J.Y., Yun, S.H., and Jeong, H.Y., (2018), A review on volcanic gas compositions related to volcanic activities and non-volcanological effects, Geosciences Journal, 22, p183-197.
[https://doi.org/10.1007/s12303-017-0056-y]

-
Lillis, R.J., Frey, H.V., Manga, M., Mitchell, D.L., Lin, R.P., Acuña, M.H., and Bougher, S.W., (2008), An improved crustal magnetic field map of Mars from electron reflectometry: Highland volcano magmatic history and the end of the martian dynamo, Icarus, 194, p575-596.
[https://doi.org/10.1016/j.icarus.2007.09.032]

-
López, T., Ushakov, S., Izbekov, P., Tassi, F., Cahill, C., Neill, O., and Werner, C., (2013), Constraints on magma processes, subsurface conditions, and total volatile flux at Bezymianny volcano in 2007-2010 from direct and remote volcanic gas measurements, Journal of Volcanology and Geothermal Research, 263, p92-107.
[https://doi.org/10.1016/j.jvolgeores.2012.10.015]

-
Notsu, K., and Mori, T., (2010), Chemical monitoring of volcanic gas using remote FT-IR spectroscopy at several active volcanoes in Japan, Applied Geochemistry, 25, p505-512.
[https://doi.org/10.1016/j.apgeochem.2010.01.008]

-
Proussevitch, A., and Sahagian, D., (2005), Bubbledrive-1: a numerical model of volcanic eruption mechanisms driven by disequilibrium magma degassing, Journal of Volcanology and Geothermal Research, 143, p89-111.
[https://doi.org/10.1016/j.jvolgeores.2004.09.012]

-
Ramírez-Ruiz, J.J., Santiago-Jiménez, H., Alatorre-Chávez, E., and Bretón-González, M., (2002), EDM deformation monitoring of the 1997-2000 activity at volcán de Colima, Journal of Volcanology and Geothermal Research, 117, p61-67.
[https://doi.org/10.1016/S0377-0273(02)00235-4]

-
Ratdomopurbo, A., and Poupinet, G., (2000), An overview of the seismicity of Merapi volcano (Java, Indonesia), 1983-1994, Journal of Volcanology and Geothermal Research, 100, p193-214.
[https://doi.org/10.1016/s0377-0273(00)00137-2]

-
Rehfeld, K., Marwan, N., Heitzig, J., and Kurths, J., (2011), Comparison of correlation analysis techniques for irregularly sampled time series, Nonlinear Processes in Geophysics, 18, p389-404.
[https://doi.org/10.5194/npg-18-389-2011]

-
Robock, A., (2000), Volcanic eruptions and climate, Reviews of Geophysics, 38, p191-219.
[https://doi.org/10.1029/1998rg000054]

-
Rosi, M., Bertagnini, A., and Landi, P., (2000), Onset of the persistent activity at Stromboli volcano (Italy), Bulletin of Volcanology, 62, p294-300.
[https://doi.org/10.1007/s004450000098]

-
Saepuloh, A., Urai, M., Aisyah, N., Sunarta, Widiwijayanti, C., Subandriyo, and Jousset, P., (2013), Interpretation of ground surface changes prior to the 2010 large eruption of Merapi volcano using ALOS/PALSAR, ASTER TIR and gas emission data, Journal of Volcanology and Geothermal Research, 261, p130-143.
[https://doi.org/10.1016/j.jvolgeores.2013.05.001]

-
Sasai, Y., Uyeshima, M., Zlotnicki, J., Utada, H., Kagiyama, T., Hashimoto, T., and Takahashi, Y., (2002), Magnetic and electric field observations during the 2000 activity of Miyake-Jima volcano, Central Japan, Earth and Planetary Science Letters, 203, p769-777.
[https://doi.org/10.1016/s0012-821x(02)00857-9]

-
Shimoike, Y., and Notsu, K., (2000), Continuous chemical monitoring of volcanic gas in Izu-Oshima volcano, Japan, Volcanology and Geothermal Research, 101, p211-221.
[https://doi.org/10.1016/s0377-0273(00)00178-5]

-
Shinohara, H., (2005), A new technique to estimate volcanic gas composition: plume measurements with a portable multi-sensor system, Journal of Volcanology and Geothermal Research, 143, p319-333.
[https://doi.org/10.1016/j.jvolgeores.2004.12.004]

-
Sponberg, M.E., (2000), Spectra analysis of base flow separation with digital filters, Water Resources Research, 36, p745-752.
[https://doi.org/10.1029/1999WR900303]

-
Stremme, W., Ortega, I., Siebe, C., and Grutter, M., (2011), Gas composition of Popocatépetl volcano between 2007 and 2008: FTIR spectroscopic measurements of an explosive event and during quiescent degassing, Earth and Planetary Science Letters, 301, p502-510.
[https://doi.org/10.1016/j.epsl.2010.11.032]

-
Symonds, R.B., Gerlach, T.M., and Reed, M.H., (2001), Magmatic gas scrubbing: implications for volcano monitoring, Journal of Volcanology and Geothermal Research, 108, p303-341.
[https://doi.org/10.1016/s0377-0273(00)00292-4]

-
Werner, C., Kelly, P.J., Doukas, M., López, T., Pfeffer, M., McGimsey, R., and Neal, C., (2013), Degassing of CO2, SO2, and H2S associated with the 2009 eruption of Redoubt volcano, Alaska, Journal of Volcanology and Geothermal Research, 259, p270-284.
[https://doi.org/10.1016/j.jvolgeores.2012.04.012]

- Wessa, P., (2017), Free Statistics Software, Office for Research Development and Education, version 1.1.23-r7, available at http://www.wessa.net/.
-
Widiyantoro, S., and van der Hilst, R., (1996), Structure and evolution of lithospheric slab beneath the Sunda Arc, Indonesia, Science, 271, p1566-1570.
[https://doi.org/10.1126/science.271.5255.1566]

-
Zimmer, M., and Erzinger, J., (2003), Continuous H2O, CO2, 222Rn and temperature measurements on Merapi volcano, Indonesia, Journal of Volcanology and Geothermal Research, 125, p25-38.
[https://doi.org/10.1016/s0377-0273(03)00087-8]